More than 5 years have passed since last update.

電子回路の内部で発生する雑音

電子回路

Last updated at 2019-08-13Posted at 2019-08-13

はじめに

IoTの開発やその他様々な事情で現実空間の情報をセンシングする必要に迫られている方は多いのではないかと思います。
センサーから高精度なアナログ情報をデジタルデータとして得るためには、雑音を減らすことが不可欠となります。雑音の性質を理解していないと泥沼の戦いになることがしばしばあります。雑音には回路の内部で発生する量子化雑音と熱雑音といったものと、回路の外部で発生するEMCなどがあります。

この記事では回路の内部で発生する定常的な雑音の性質について解説を行います。
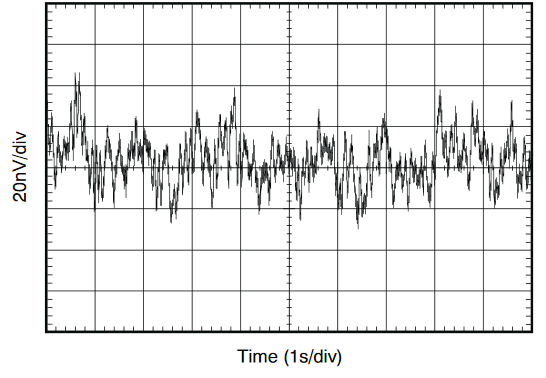
典型的な雑音の電圧波形を示します。

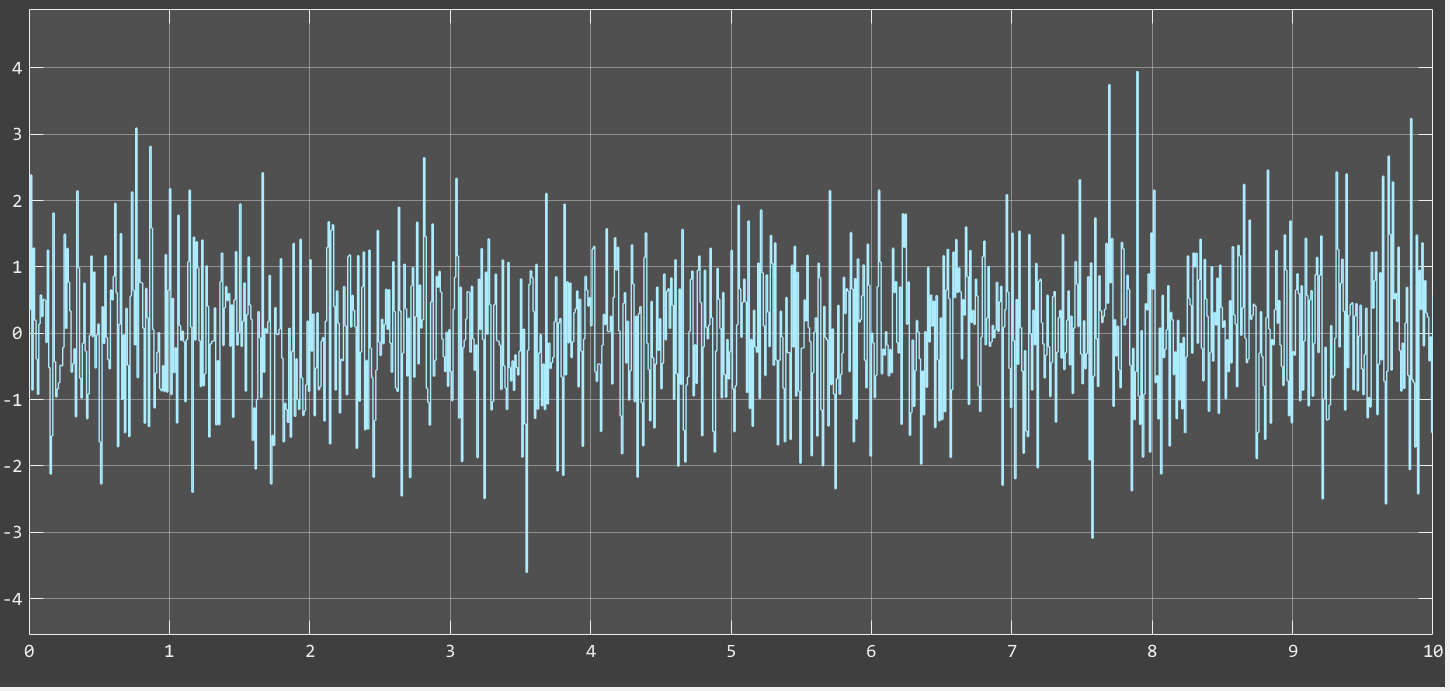
雑音の単位

ほとんどの場合、雑音電圧は瞬時値$v_n$に対して電圧の二乗平均$\overline{v_n^2} \;\mathrm{(V_{rms}^2)}$か二乗平均平方根$v_{n,rms}(=\sqrt{\overline{v_n^2}})\;\mathrm{(V_{rms})}$で表されます。これは雑音は統計的性質を持っており、雑音電圧が正規分布をしている場合ピークtoピーク電圧は無限大となってしまい扱いづらいためです。
実時間軸上で、定常的な雑音の瞬時値$v_n$に対して二乗平均は以下のように表されます。

\overline{v_n^2} = \lim_{T \to \infty} \frac{1}{2T}\int_{-T}^{T}v_n^2\:dt

雑音電圧が正規分布の広がりを持ち、$v_{n,rms}$が1の場合、雑音電圧の分布は以下のようになります。

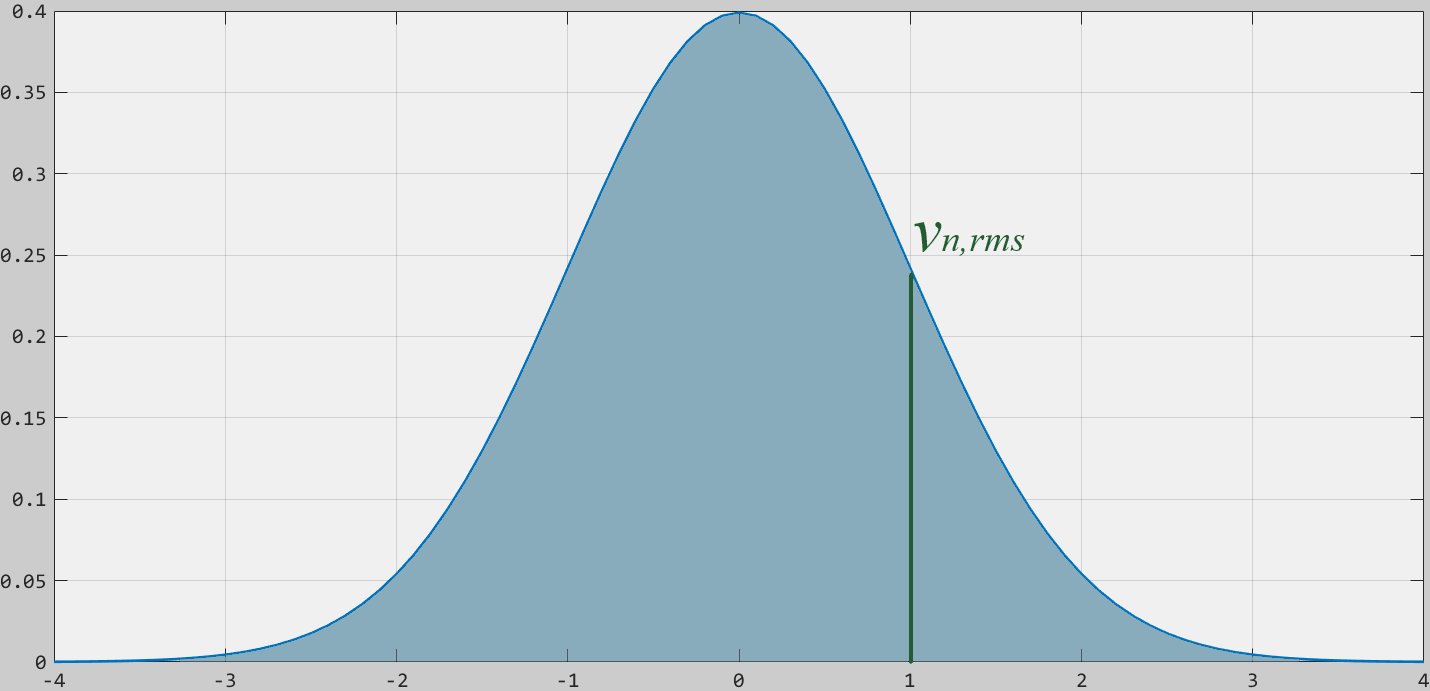
$\pm3.3\ v_{n,rms}$の範囲に約99.9%の雑音が収まるので便宜的に$v_{n,rms}$の6.6倍を雑音のピークtoピーク電圧とする場合もあります。
雑音は多くの場合周波数軸上で広がりを持つため、1Hzの帯域幅内に存在する雑音電力または雑音電圧の密度としての表現もよくつかわれます。

e_n^2 \; \mathrm{(V^2/Hz)}\\
e_n \; \mathrm{(V/\sqrt{Hz})}

$f_1$から$f_2$までの周波数帯域の雑音電圧は雑音密度を積分して得られます¹。

\overline{v_n^2} = \int_{f_1}^{f_2}e_n^2 \: df \\
v_{n,rms}=\sqrt{\int_{f_1}^{f_2}e_n^2 \: df}\; \mathrm{(V_{rms})}

以下に示すように雑音密度の周波数分布の面積から雑音の振幅を求めることができます。

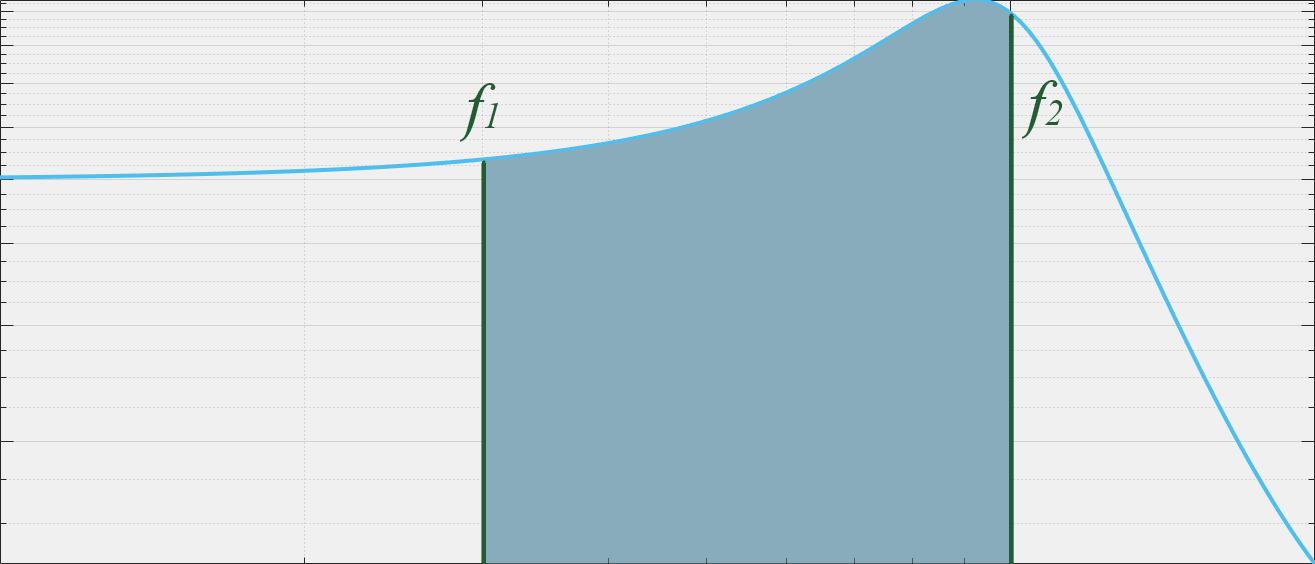
互いに相関性のない複数の雑音電圧を加算するときは二乗和の平方根をとる必要があります。

v_{n,total} = \sqrt{v_{n1}^2+v_{n2}^2+v_{n3}^2+v_{n4}^2+...}

熱雑音とは

導体、絶縁体問わず全ての回路素子には熱エネルギーによ起因する1Hzあたり$4kT$の熱雑音電力が発生します($k$はボルツマン定数、Tは絶対温度)。
この熱雑音電力が抵抗$R$で電圧に変換されたとき、抵抗両端の電圧は

e_{Tn} = \sqrt{4kTR} \; \mathrm{(V/\sqrt{Hz})}

の雑音電圧密度となります²³。温度300Kにおける抵抗と熱雑音の関係を示します。

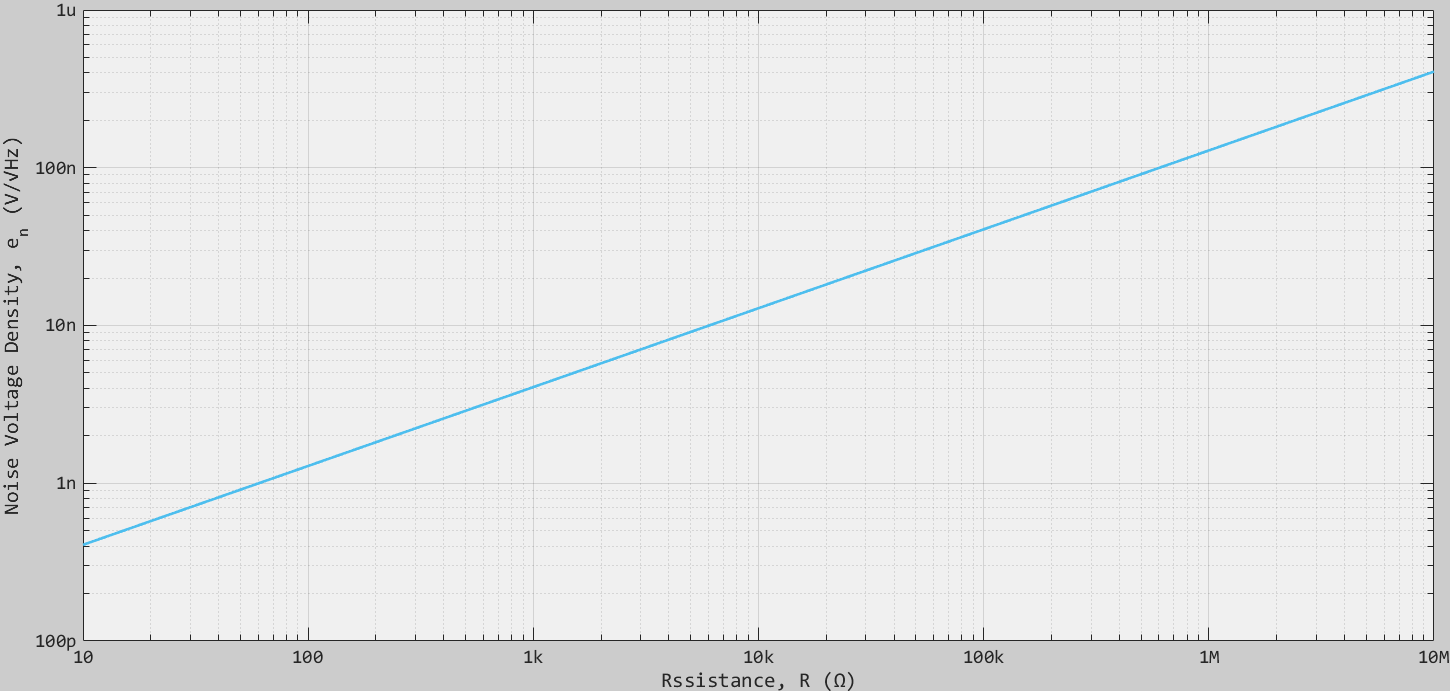
抵抗の熱雑音は全ての周波数で均一に発生するので雑音密度のグラフは周波数軸に並行となります。また、帯域$B$での雑音振幅は

v_{Tn,rms} = \sqrt{4kTRB} \; \mathrm{(V_{rms})}

となります。
例として室温では$1\,\mathrm{k\Omega}$ の抵抗の雑音電圧密度は約$4\,\mathrm{nV/\sqrt{Hz}}$、帯域$10\,\mathrm{kHz}$であれば振幅は約$0.4\,\mathrm{\mu V_{rms}}$となります。

フリッカ雑音とは

主にトランジスタやオペアンプなどの半導体素子の低周波の雑音特性に影響します。雑音電力密度のグラフが1/fの傾きを持つことから1/f雑音とも呼ばれています。勘違いしがちですが雑音電圧密度は1/√fの傾きになるので気をつけてください。
フリッカ雑音は複数の発生源があり重なり合っていると言われていますがそのうちの一つを紹介します。

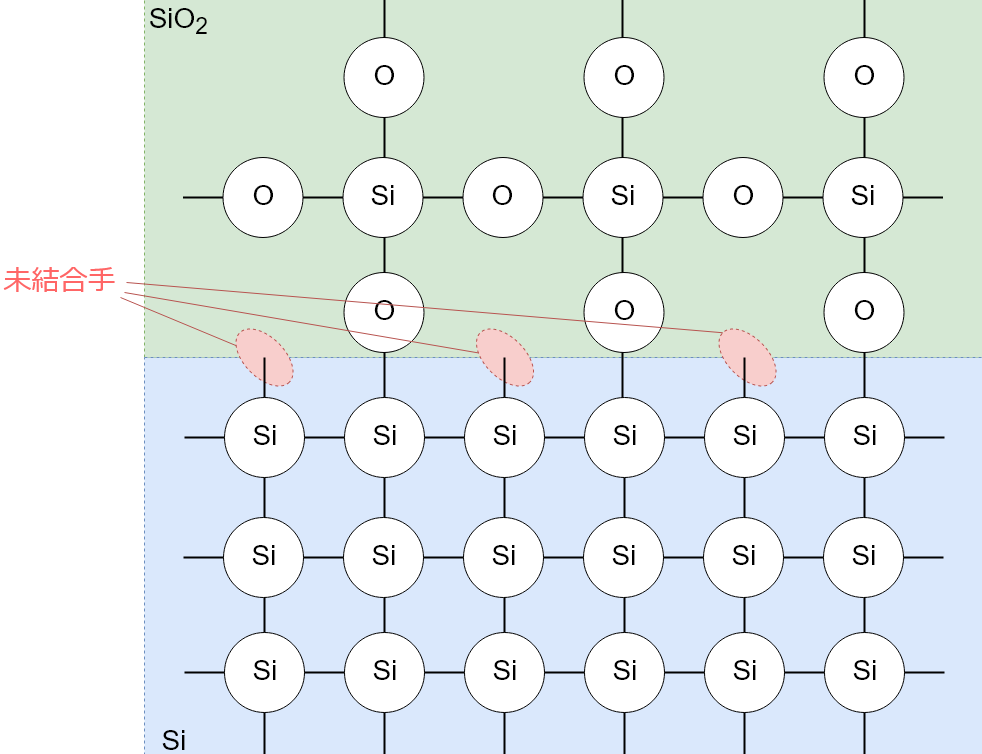
フリッカ雑音はMOS-FETでは比較的大きく、バイポーラトランジスタでは比較的小さいものとなります。これは電流がSi結晶のどこを流れるかが異なるためです。
Siはダイヤモンド結晶構造の非常に欠陥の少ない単分子結晶となるのですが、結晶の表面や酸化膜との界面は結晶構造が途切れてしまいます。このため未結合手（ダングリングボンド）が大量にある非常に欠陥の多い構造となっています。未結合手が気まぐれに（ばらつきのある時定数を持って）電子の捕獲や放出を行い、これがフリッカ雑音の原因となります⁴。

プレーナー構造のMOSFETは基本的にSiとSiO2の界面付近を電流が流れるので雑音が大きくなります。一方でバイポーラトランジスタはSi内部を電流が流れるために相対的にフリッカ雑音が小さくなります。

オペアンプの入力換算雑音

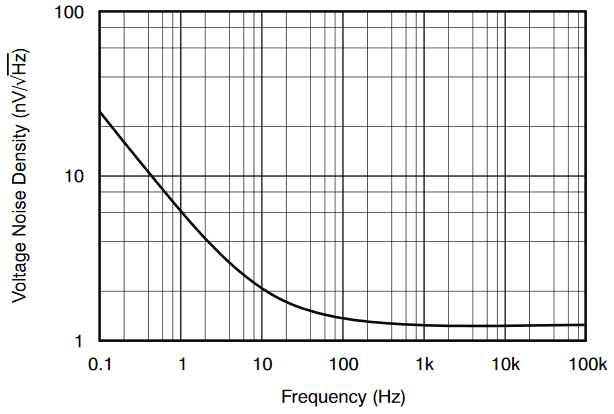
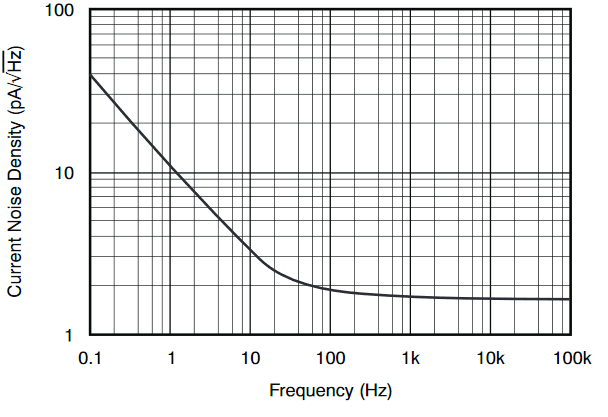
市販のオペアンプのデータシートには入力換算雑音電圧密度と入力換算雑音電流密度のデータが記述されていることがあります。ほとんどのオペアンプでは1kHz以上では熱雑音が、10Hz以下ではフリッカ雑音が支配的になることから1KHzでの雑音密度及び0.1-10Hzでの雑音電圧がスペックとして記述されていることが多いです。OPA211のデータシート⁵から引用した雑音電圧密度、雑音電流密度、0.1-10Hz雑音波形を示します。

オペアンプの入力換算雑音から実際に出力される雑音を計算するには少し複雑な計算手順が必要になります⁶。

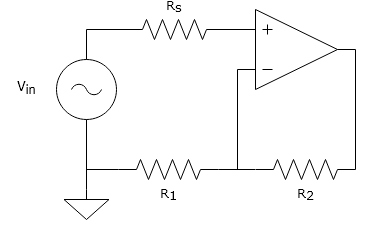
電圧$V_{in}$、出力インピーダンス$R_s$を接続した非反転増幅回路の雑音を計算します。面倒なのでオペアンプは入力換算雑音を持つこと以外、理想オペアンプであると仮定します。
この回路での出力電圧は

v_{out} = (1+\frac{R_2}{R_1})V_{in}

となります。

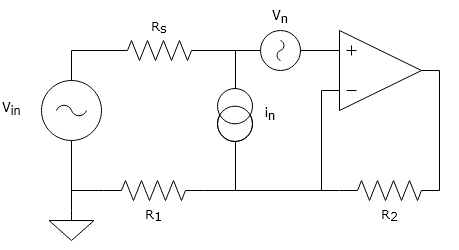
オペアンプの入力換算電圧雑音と入力換算電流雑音は以下のように定義できます。

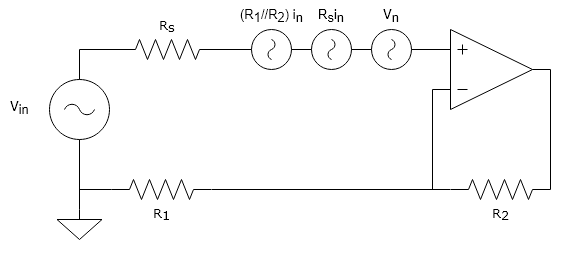
イマジナリーショートとテブナンの定理から電圧に変換して非反転入力側に集めます。

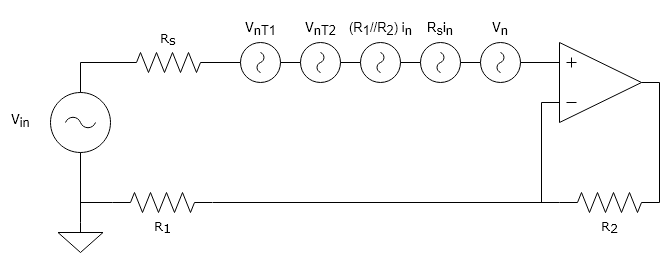
ソース抵抗、フィードバック抵抗による熱雑音を加算します$(v_{nT1}=\sqrt{4kTR_s},\,v_{nT2}=\sqrt{4kT(R_1//R_2)})$。

よってこの回路で出力される雑音は

v_{n,out} = (1+\frac{R_2}{R_1})\sqrt{v_{nT1}^2+v_{nT2}^2+((R_1//R_2)i_n)^2+(R_si_n)^2+v_n^2}

となります。
注意点として抵抗両端の熱雑音電圧は抵抗値Rの平方根に比例しますが、オペアンプの入力換算雑音電流による雑音電圧は信号源抵抗のRに比例します。また、雑音電圧と雑音電流はトレードオフの関係にあり、信号源インピーダンスに合わせて適切な雑音特性のオペアンプを選択する必要があります。
初段の入力トランジスタがバイポーラトランジスタの場合は雑音電圧が小さめ、雑音電流が大きめに、FETの場合は雑音電圧が大きめ、雑音電流が小さめとなる傾向があります。またFETの中でもMOS-FET入力のものはJ-FET入力と比較してフリッカ雑音が大きくなる傾向があります。

バイポーラ入力の低雑音オペアンプであるOPA211(雑音特性はOPA1612と同等)とJFET入力の低雑音オペアンプであるOPA1656のソース抵抗に対する室温、1kHzにおける雑音電圧を示します⁵⁷。

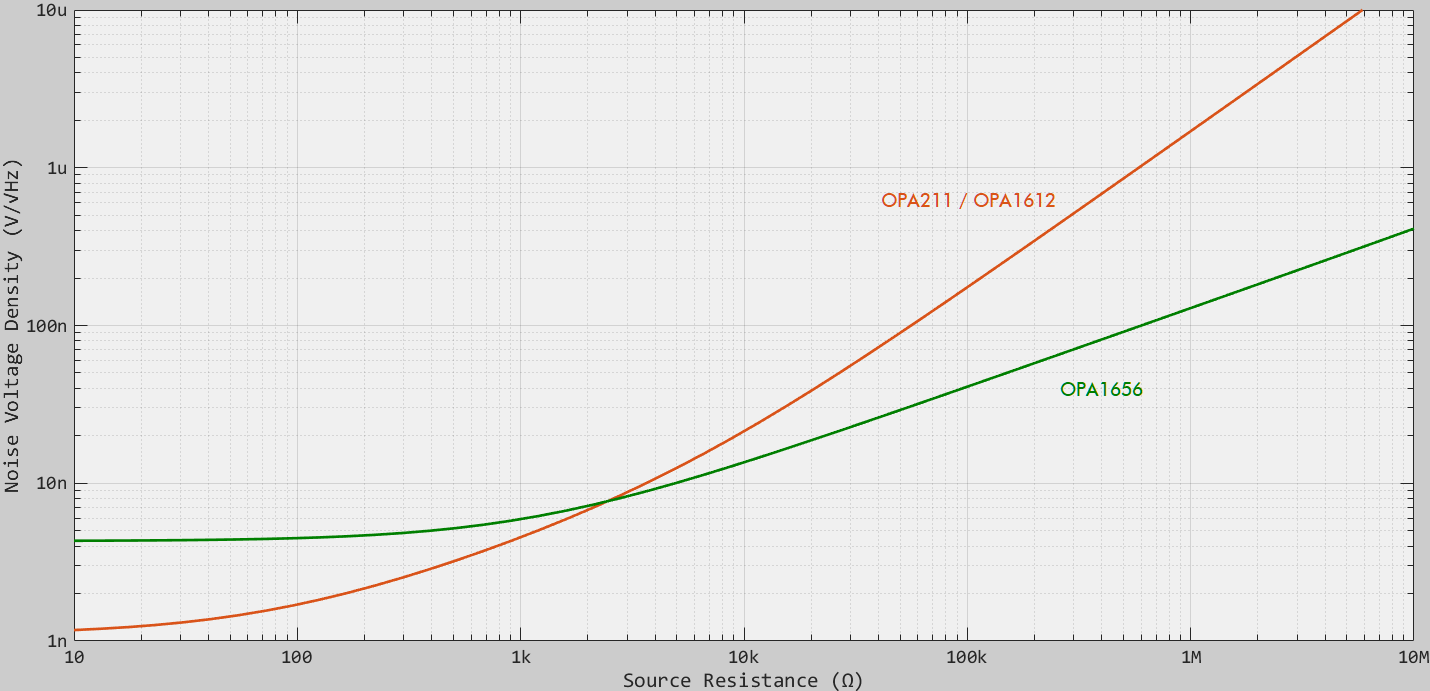
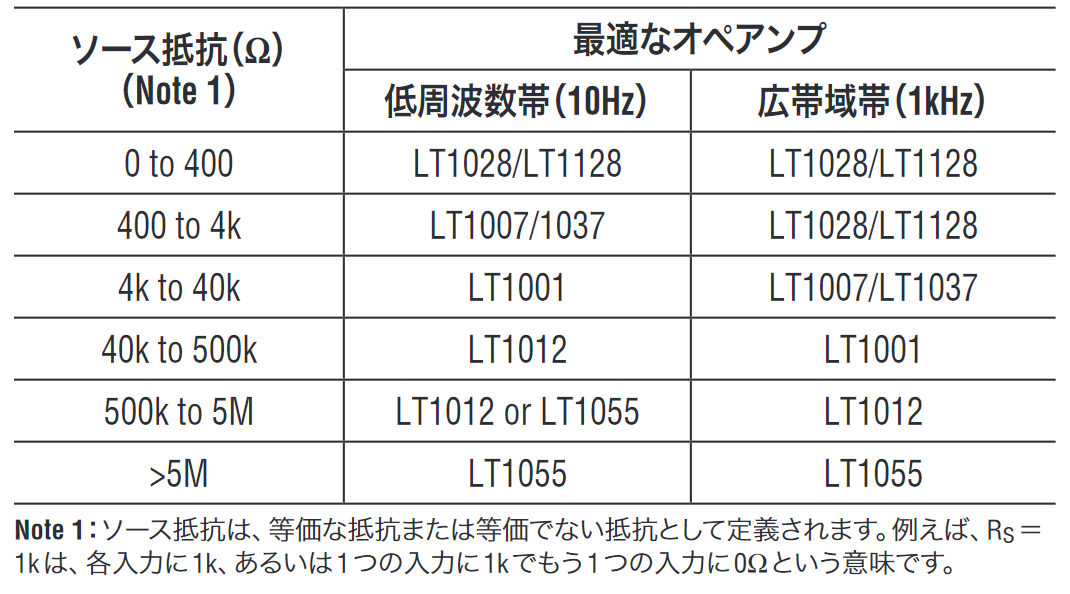
ソース抵抗が2.5kΩ以下の場合はOPA211が、2.5kΩ以上の場合はOPA1656が低雑音な特性となります。これらの関係は温度や帯域によって変化する可能性があるので注意が必要です。参考としてLinear Technologyではデータシート⁸に帯域別で低雑音となる推奨オペアンプを示しています。

参考文献

黒田徹, 解析OPアンプ&トランジスタ活用, 2002, CQ出版
Paul Horowitz, Winfield Hill, The Art of Electronics, 2015, Cambridge University Press

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up