何の記事か
今回はセグメント木(Segment Tree)というデータ構造について、勉強したことをまとめてみた。
参考書として使ったのは蟻本。だいだい内容は同じだ。
概要、それらを使ってできること、実装の順で説明してある。
セグメント木
何それ
セグメント木は具体的に以下の画像のようなデータ構造になっている。
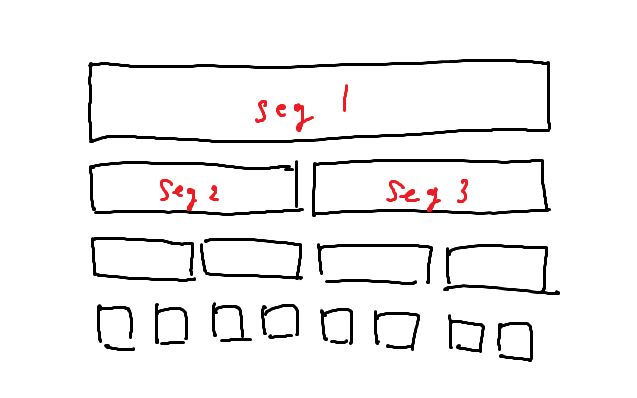
それぞれの要素は、対応する数列の区間の何かしらのデータを管理している。
構造的には完全二分木になっているので、$O(logN)$で動作する高速なデータ構造を実現できる。
解きたい問題における数列を{$a_i$}とすれば、{$a_i|i=s~t$}に対して求めたいある値を$O(logN)$で求めることができるというわけである。
今回は RMQ(Range Minimum Query) を解くことを考えることにする。
つまり、『{$a_i|i=s~t$}の最小値を求めるクエリを高速に処理する』ことを考えるために、セグメント木を用いることにする。
RMQ
数列のある区間に対して、その中の要素の最小値を求めるクエリのこと。
できること
数列 {$a_i$}が与えられたときに、以下の操作を$O(logN)$で行うことができる。
- $s$と$i$が与えられた時、{$a_i|i=s~t$}の最小値を求める
- $a_i$の値を更新する
では本当にこれらの操作を$O(logN)$で行えるのだろうか。
図を見てもらった方が分かりやすいと思うので、図を描いてみた。今回のセグメント木のデータ数は$2^4$としてある。
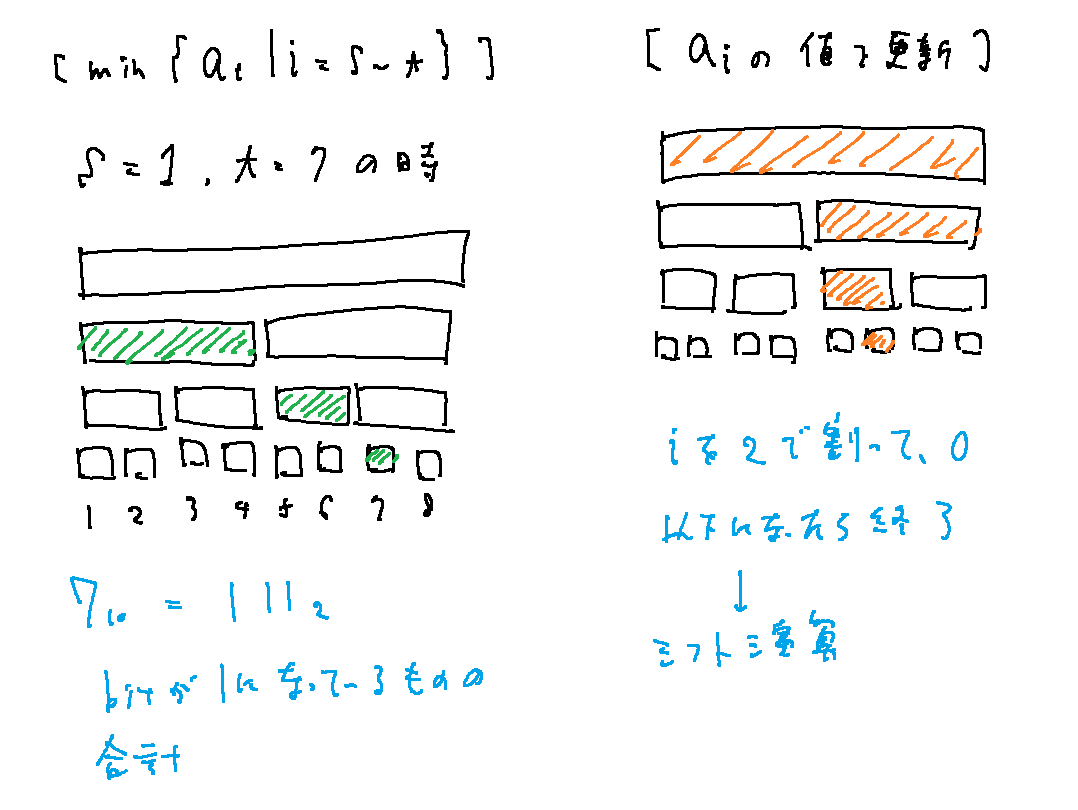
最小値を求める操作では、普通に解こうとすると、$O(N)$となってしまうことは自明だろう。
しかし、セグメント木を用いた解法では、図のように『予め最小値を求めておいた区間』を利用することで、一回の参照でも大部分の処理を行うことができている。
具体的には $t-s$ を、できるだけ大きい$2^x$から順にみていく操作になっているので、計算量が$O(logN)$となるわけである。
値を更新していく操作は、子から親へとどんどん値を上に向かって更新していく操作になっている。
計算量は、$i$に対してシフト演算を行うときと等しいことは明らかなので、$O(logN)$となる。
シフト演算
ある数 $x$ を右または左に1bitずらす操作のこと。
たとえば7(2進数で111)を右にシフトすると、3(011)となり、左にシフトすると14(1110)となる。
直感的には2で割ったり2を掛ける操作だと思っておけばよい。
どうやって実装するの
残念ながら、セグメント木はSTLで提供されるデータ構造ではない。
なので、自分で1から実装を行う必要がある。
static const int max_n = 1 << 15; //数列a_iの最大の要素数を設定する
int seg_tree[2 * max_n];
int n;
//初期化を行う関数
void init(int n_) {
//完全二分木にするため、データ数を2の倍数にする。
n = 1;
while (n < n_) n *= 2;
//RMQを考えたいので、セグ木の各値はINT_MAXに設定しておく
rep(i, 2 * n)seg_tree[i] = INT_MAX;
}
//index番目の値をxに変更する関数
void update(int index, int x) {
index += n - 1; //最も下のレイヤーにおいて、1番目の値はseg_treeの中ではn番目だから
seg_tree[index] = x;
while (index > 0) {
index = (index - 1) / 2; //親のノードのindex
seg_tree[index] = min(seg_tree[2 * index + 1], seg_tree[2 * index + 2]);
}
}
//区間[a,b)における最小値を求める関数
//indexはseg_treeにおける番号で、left,rightはseg_tree[index]の区間に対応
//query(a,b,0,0,n)として呼ぶことを考える。
int query(int a, int b, int index, int left, int right) {
//考えようとしている区間が、[a,b)に全く含まれないなら、INT_MAXを返して、操作に影響しないようにする。
if (a >= right || b <= left) return INT_MAX;
//考えようとしている区間が[a,b)に完全に含まれているなら、その値を返せばよい。
if (a <= left && b >= right) return seg_tree[index];
//どちらでもない場合、seg_tree[index]の2つの子ノードに対して再帰的に操作を行う。
int value_1 = query(a, b, 2 * index + 1, left, (left + right) / 2);
int value_2 = query(a, b, 2 * index + 2, (left + right) / 2, right);
return min(value_1, value_2);
}