はじめに
初めまして、現在0からPythonを学んでいる初心者エンジニアです。
この投稿は私が学んだことのアウトプットの場として、そして私と同じ初心者エンジニアさんの少しでも役に立てればと思い、投稿しています。私自身も全くの初心者なので、感想やアドバイスあれば、気軽にコメント頂けると幸いです。
ポアソン分布とは
今回はポアソン分布の説明を書きたいと思います。
ポアソン分布とは一定期間に発生する稀な事象の回数を表す離散確率分布で、単位時間の中で平均$\lambda$回発生する事象がk回(k=0,1,2,...)発生する確率を表現するのに用いられ、
P(X=k)=e^{-\lambda}\frac{\lambda^k}{k!}
と、表すことができます。
上記の式にはkは自然数(0,1,2,...)、eは自然対数の底(=2.71828...,ネイピア数ともいう)で、$0!=1$という約束があります。
そして上記の式が成り立つ時、このポアソン分布は$X\sim Po(\lambda)$と表すことができます。
歴史的には1年あたり平均0.61人の兵士が馬に蹴られて死ぬ軍隊において、「1年に何人の兵士が馬に蹴られて死ぬのかの確率分布」を求めたのが歴史上初めてポアソン分布が使われた事例だと言われています。
以来、ポアソン分布は主に「交通事故発生確率」や「単位時間あたりのWebサーバへのアクセス数」などに適用されています。
ポアソン分布の導出
ある一定期間をn等分し、この期間内に事象が起こる期待値が $\lambda$ 回だとすると、等分された各範囲に事象が起こる確率は $p=\frac{\lambda}{n}$ なので、この事象の発生確率は、二項分布 $B(n,\frac{\lambda}{n})$ に従い
P(X=k)={}_n C_k \left( \frac{\lambda}{n}\right)^k\left( 1-\frac{\lambda}{n}\right)^{n-k}
となります。このnの範囲を極限まで小さくする$(n→\infty)$と
\begin{eqnarray}
\lim_{n\to\infty}{}_n C_k \left( \frac{\lambda}{n}\right)^k\left( 1-\frac{\lambda}{n}\right)^{n-k}&=&\lim_{n\to\infty}\frac{n(n-1)\cdots(n-k+1)}{k!} \frac{\lambda^k}{n^k}\left( 1-\frac{\lambda}{n}\right)^n\left( 1-\frac{\lambda}{n}\right)^{-k}\\
&=& \lim_{n\to\infty}\frac{\lambda^k}{k!}\left( 1-\frac{\lambda}{n}\right)^n\left( 1-\frac{1}{n}\right)\left( 1-\frac{2}{n}\right)\cdots \left( 1-\frac{k-1}{n}\right)\left( 1-\frac{\lambda}{n}\right)^{-k}\\
\textrm{ここで}\left( 1-\frac{1}{n}\right)以降の式&が&(n→\infty) \textrm{の時、すべて1になるので}\\
&=&\lim_{n\to\infty}\frac{\lambda^k}{k!}\left( 1-\frac{\lambda}{n}\right)^n\\
&=&e^{-\lambda}\frac{\lambda^k}{k!}
\end{eqnarray}
と、導出することができます。
要するにポアソン分布は二項分布の極限のようなものです
そして、上記の式を用いることにより、ポアソン分布の期待値と分散を求めることができます。
ポアソン分布の期待値
\begin{eqnarray}
E(X)&=&\sum_{k=0}^n kP(X=k) \\
&=&\sum_{k=0}^n k\frac{\lambda^ke^{-\lambda}}{k!} \\
&=&\sum_{k=0}^n \frac{\lambda^ke^{-\lambda}}{(k-1)!} \\
&=&\lambda\sum_{k=0}^n \frac{\lambda^{k-1}e^{-\lambda}}{(k-1)!}\\
&=&\lambda\\
\end{eqnarray}
ポアソン分布の分散
\begin{eqnarray}
E(X^2)&=&\sum_{k=0}^n k^2P(X=k) \\
&=&\sum_{k=0}^n k^2\frac{\lambda^ke^{-\lambda}}{k!} \\
&=&\sum_{k=0}^n (k(k-1)+k)\frac{\lambda^ke^{-\lambda}}{k!} \\
&=&\sum_{k=0}^n k(k-1)\frac{\lambda^ke^{-\lambda}}{k!} +\sum_{k=0}^n k\frac{\lambda^ke^{-\lambda}}{k!}\\
&=&\sum_{k=0}^n \frac{\lambda^ke^{-\lambda}}{(k-2)!}+\lambda\\
&=&\lambda^2\sum_{k=0}^n \frac{\lambda^{k-2}e^{-\lambda}}{(k-2)!}+\lambda\\
&=&\lambda^2+\lambda\\
\\
V(X)&=&E(X^2)-(E(X))^2\\
&=&\lambda^2+\lambda-\lambda^2\\
&=&\lambda
\end{eqnarray}
となり、ポアソン分布の期待値も分散も$\lambda$になることがわかります。これもポアソン分布の大事な特徴の一つなのでぜひ覚えましょう。
ポアソン分布に従う確率変数の性質
ポアソン分布に従う確率変数は次の性質を満たしている必要があります。
1.(独立性)事象が起きるのは互いに独立である。
2.(定常性)事象が起きる確率はどの時間帯でも同じである。
3.(希少性)微笑時間tの間にその事象が2回以上起きる確率は無視できるくらい小さいとする。
この3つの性質に関してもう少し掘り下げていきます。
1.独立性
独立性とは、2つ以上の事象が互いに影響を与えず、それぞれが独立して発生する性質のことを指します。要するに、ある事象が起こる確率がその他の事象の結果に影響を受けず、常に一定ということです。
例えば、サイコロを1つ振って6が出る確率は常に$\frac{1}{6}$であり、前の結果には依存しません。
2.定常性
定常性とは、時系列データが時間の経過に伴って統計的性質が変化しないことを指します。要するに、ある事象が起こる確率が季節や時間帯によって影響を受けないということです。
例えば、1日の暖房の使用時間だと季節によってバラバラなので、過去のデータから将来のデータを予測することは困難です。なので例えば、単位時間あたりにATMに訪れるお客さんの数などは時間や曜日によって変動することもありますが、大きな変動は起こらず、長期的な傾向において一定の範囲内に収まることが多いです。
3.希少性
ある時間や空間において、事象が発生する回数が少なく、稀であることを指します。要するに一度に事象が複数回起こってしまうと、発生率が定まらなくなってしまうので、ポアソン分布はあくまでも稀な事象がk回起こる確率を表すため、希少性を満たす必要があります。
これらの性質を全て満たす確率変数をポアソン分布では扱います。
ポアソン分布のグラフ
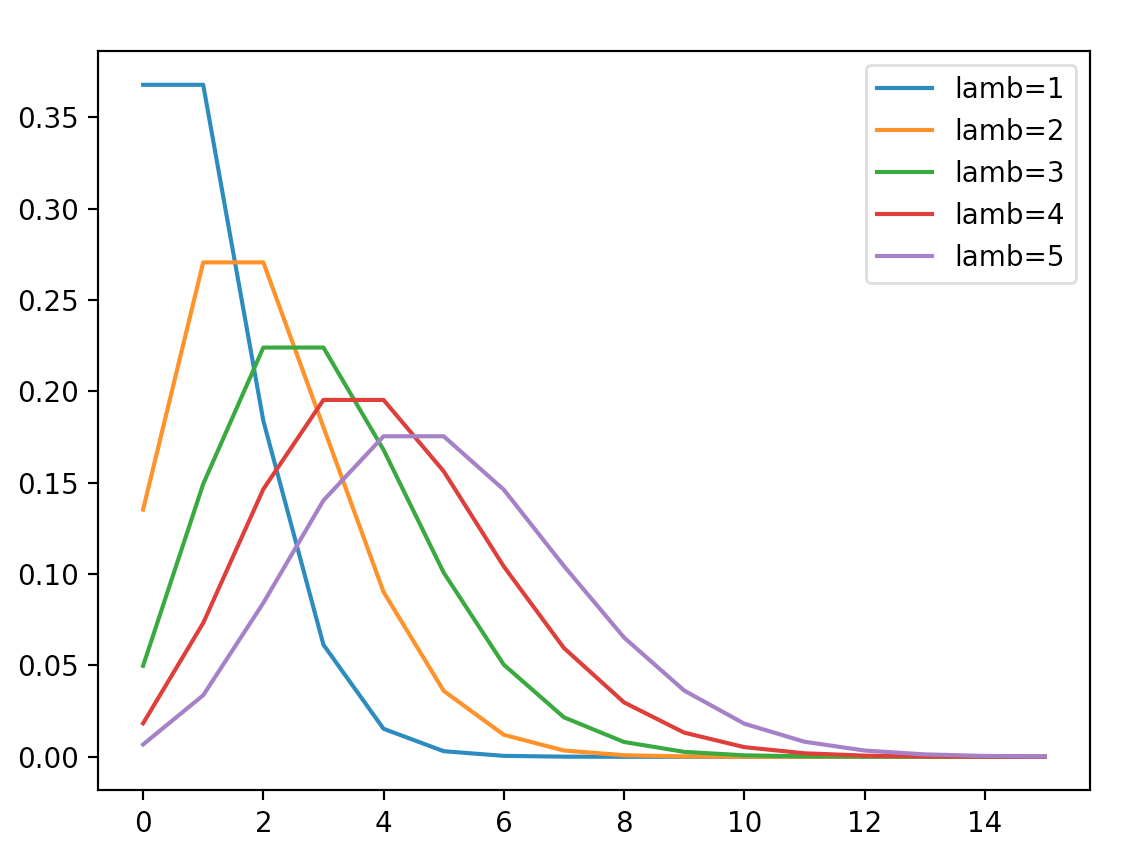
$\lambda$を変数としたときのポアソン分布$P(X=k),(k=0,1,2,...,15)$の場合のグラフを得るコードを次に示します。
import numpy as np # ベクトル演算などに用いる
import matplotlib.pyplot as plt # グラフの生成に用いる
from scipy.stats import poisson # ポアソン分布を利用する
k=np.arange(0,16) # 0から15まで1ずつkをとる(16は含まれない)
for lamb in range(1,6): # lambが1から5まで繰り返し処理を行う(range()は整数型のみ対応)
p=poisson.pmf(k,lamb) # 平均lamb回発生する事象がk回発生する確率(これがポアソン分布)
plt.plot(k,p,label="lamb="+str(lamb)) # lambの値をラベルに表示
plt.legend() # グラフに凡例を表示
else: plt.show() # グラフを表示
ここで
poisson.pmf(k,lamb)
は平均lamb回発生する事象がk回発生する確率を計算してくれる関数を意味します。(要するにポアソン分布の確率の計算を行なってくれる関数です。)
このような図になり、$\lambda$が大きくなるにつれて、分布がなだらかかつ右に移行することがわかります。これは上記したポアソン分布の分散が$V(X)=\lambda$なことが影響します。(分散が大きいと値にばらつきが出るので)
まとめ
以上が、ポアソン分布の説明になります。次回以降に実際の例を用いて計算を行っていきたいと思います。
最後まで読んで頂きありがとうございました。引き続き私と一緒に研鑽していきましょう。
参考
橋本洋志,牧野浩二."データサイエンス教本 Pythonで学ぶ統計分析・パターン認識・深層学習・信号処理・時系列データ分析".オーム社,2018
ポアソン分布の導出
ポアソン分布とは何か。その性質と使い方を例題から解説