本日は R によるやさしい統計学の第 10 章「外れ値が相関係数に及ぼす影響」の内容を参考に pandas でデータの相関関係を調べながら外れ値を取り除いていく方法を説明します。元の書籍では R を利用していますが pandas を使えばその代替として Python においてもデータフレームを利用した分析を簡単におこなうことができます。
動物の体重と脳の重さを調べる
元の書籍の通り動物の体重と重さに関するデータを利用します。
まずはこれを先日と同じく計算機で取り扱えるよう CSV のデータとして用意しました。
CSV のデータをデータフレームに取り込みます。
animal = pd.read_csv('animal.csv')
散布図を描き相関係数を求める
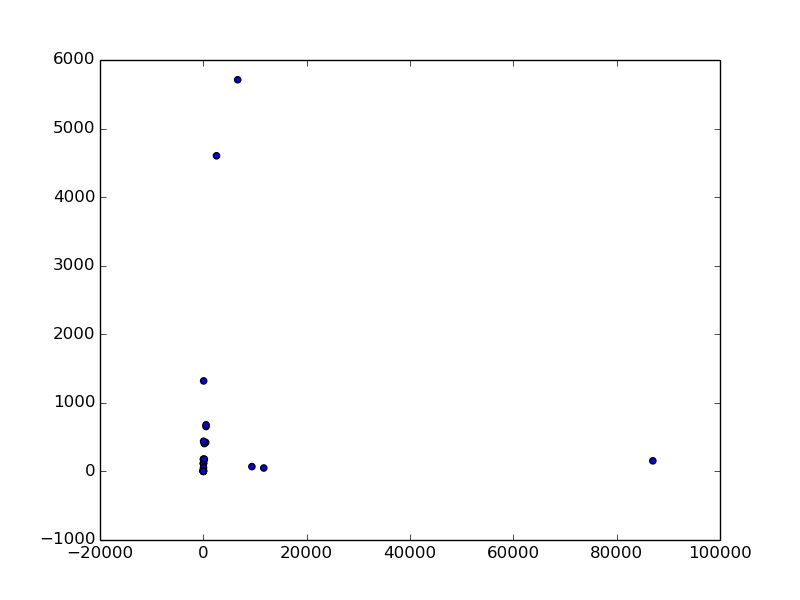
2 つの変数がありその相関を調べる場合、まずは散布図にして眺めることが最初のステップです。散布図の描き方は以前にも説明した通りです。さっそくやってみます。
plt.figure()
plt.scatter(animal.ix[:,1], animal.ix[:,2])
plt.savefig('animal.png')
さらにいつも通り相関係数を求めます。
animal.corr()
# =>
# Body weight (kg) Brain weight (g)
# Body weight (kg) 1.000000 -0.005341
# Brain weight (g) -0.005341 1.000000
元書籍の 250 ページにあるように相関係数 -0.005 という値が求まりました。このままでは相関関係はほとんど無いことになります。
外れ値の除去をする
外れ値の調べ方については以前にも説明した通りですが、元の書籍の R のコードにしたがって外れ値を特定し除去していきます。まず上の散布図の右側に 1 つだけ点があります。これはデータの 24 番にある Brachiosaurus というブラキオサウルスという恐竜で、体重が 80,000 kg もあるのに脳の重さが 1,000 g に満たないというデータです。これを取り除きましょう。
# 体重が 80000 未満のデータのみを選択する
animal2 = animal[animal.ix[:,1] < 80000]
これは脳の重さが 80000 未満のデータを選択するという意味です。なおインデックス参照を付けないとデータのうち 80000 に満たないデータのみが残り、該当しないデータは NaN になります。ですから、こう書いても結果的には一緒です。
animal2 = animal[animal < 80000].dropna()
この状態で散布図を描き相関係数を求めてみます。
animal2.corr()
# =>
# Body weight (kg) Brain weight (g)
# Body weight (kg) 1.000000 0.308243
# Brain weight (g) 0.308243 1.000000
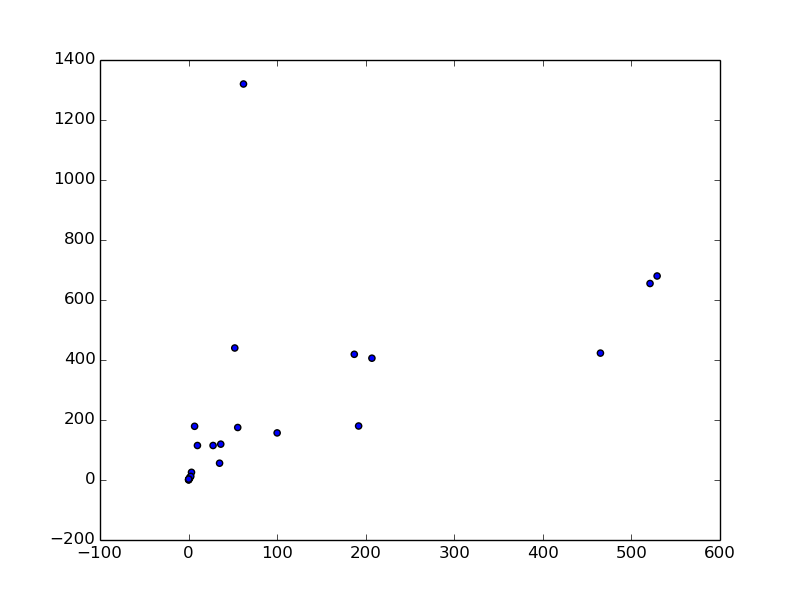
相関係数が 0.30 になりました。やや弱い正の相関があることになります。さらに元書籍の通り今度は体重が 2,000 kg 以上の 4 つの動物を取り除いてみます。
animal2 = animal[animal.ix[:,1] < 2000]
animal2.corr()
# =>
# Body weight (kg) Brain weight (g)
# Body weight (kg) 1.000000 0.542351
# Brain weight (g) 0.542351 1.000000
plt.scatter(animal2.ix[:,1], animal2.ix[:,2])
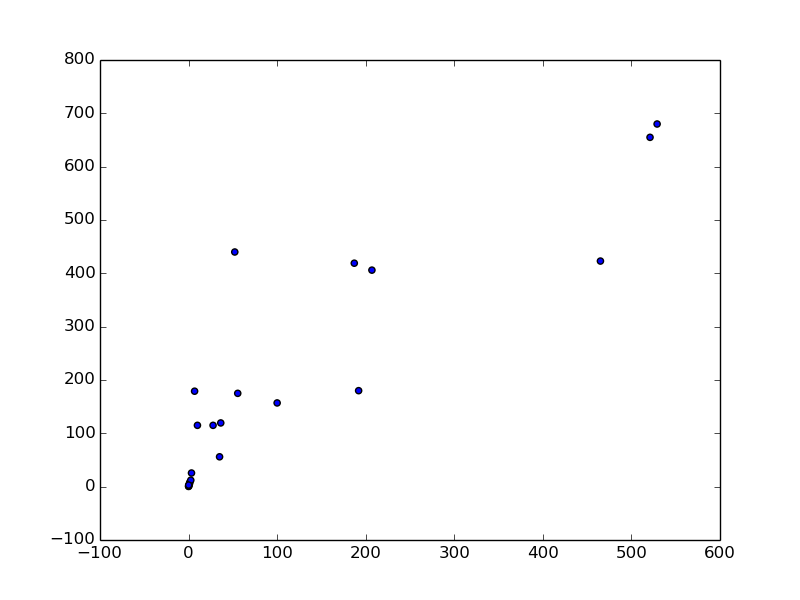
今度は相関係数が 0.54 まで上昇しました。散布図の左上に 1 つだけ外れ値があるのが目視できます。これは人間で、体重 100 kg 未満で脳の重さが 1,200 g を越えています。他の動物と比較しても人間は体重に対する脳の重さの割合が非常に突出していることがわかります。
人間も除去するとどうなるでしょうか。脳の重さが 1,000g 未満の動物に絞ってもう一度調べてみましょう。
animal3 = animal2[animal2.ix[:,2] < 1000]
# 相関係数を求める
animal3.corr()
# =>
# Body weight (kg) Brain weight (g)
# Body weight (kg) 1.000000 0.882234
# Brain weight (g) 0.882234 1.000000
相関係数は 0.88 となります。このことから一部の動物を除くと、脳の重さと体重に強い正の相関があることがわかりました。
線形回帰をする
元の書籍にはありませんが、せっかく強い正の相関が得られましたから回帰式を求めてみましょう。
from scipy import stats
stats.linregress(animal3.ix[:,1], animal3.ix[:,2])
# => (1.0958855201992723,
# 68.659009180996094,
# 0.88223361379712761,
# 5.648035643926062e-08,
# 0.13077177749121441)
SciPy のドキュメントにある通り scipy.stats.linregress の戻り値はそれぞれ傾き、切片、相関係数、 P 値、標準誤差です。
したがいまして求める回帰式 (少数第 2位まで) は以下の通りです。
y = 1.10x + 68.66
また P 値が非常に小さい値であることがわかります。
まとめ
統計を利用した主な 2 つのデータ分析を挙げるとするなら仮説検定と相関分析であると言っても差し支えないくらいでしょう。 (もちろん色々言えば他にもありますが)
先日や今回はいわゆる相関分析をおこなったわけですが、このように 2 つの変数について相関があるかどうかを調べることは統計の基礎となります。
どういったことが関係があると考えられるか、しっかりと仮説を立ててデータ分析に挑むことで、関係性が統計学的にどうであるのか結果を出すことができます。
次回は久しぶりにもうひとつの主な統計学的手法である仮説検定について整理をしてみます。