プレジデントオンラインに統計の記事が掲載されていました。
朝食や出社時間と、営業成績に「相関関係」はあるか?
http://president.jp/articles/-/12416
上記の記事では確かに数式は出てこないのでとっつきやすく解説は詳しいので統計の入門にはピッタリです。しかしながらエクセルで手計算することが前提になっておりこれは若干億劫です。
そこで今まで利用してきた Python でこれらの問題を計算してみたいと思います。
問題とその解法
問題の内容としては各社員の、朝食を食べてきた確率 (= 朝食率) 、出社時間、それに対して営業成績を 3 つの変数として相関関係があるか調べるというものです。このように変数の間の相関関係を調べるというのはさまざまな統計の基本とも言えるでしょう。
計算機で扱えるように、それぞれの変数を X Y Z としましょう。まずはこれをCSV ファイルのデータとして用意しました。
基本統計量を算出する
まずは 2 ページ目に登場する統計量を求めます。上記のデータを読み込んで平均や標準偏差などの基本統計量を求めます。これは pandas を使えば簡単で、一瞬で求まります。
data = pd.read_csv("data.csv", names=['X', 'Y', 'Z'])
data.describe()
# =>
# X Y Z
# count 7.000000 7.000000 7.000000
# mean 42.571429 -8.571429 98.714286
# std 42.968427 14.920424 8.440266
# min 0.000000 -40.000000 88.000000
# 25% 5.000000 -10.000000 92.000000
# 50% 33.000000 -5.000000 100.000000
# 75% 77.500000 0.000000 104.500000
# max 100.000000 5.000000 110.000000
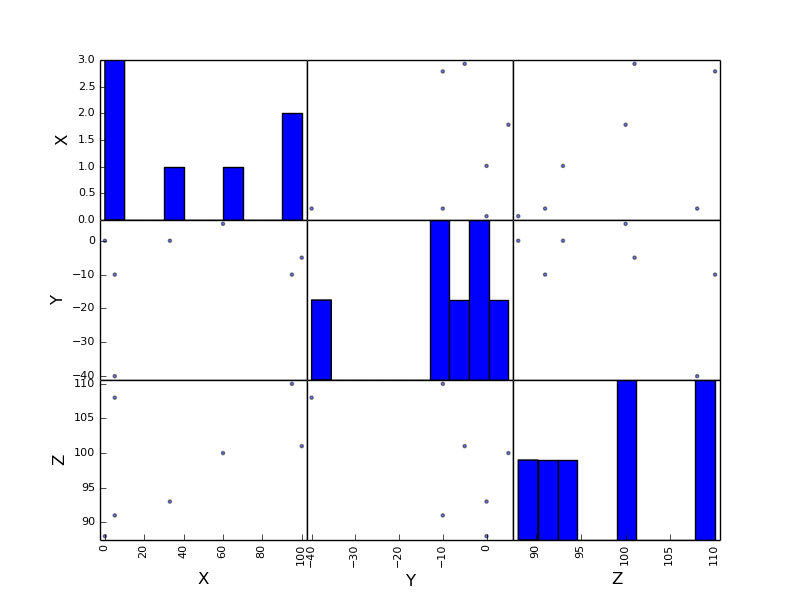
散布図行列を描く
元の記事では散布図を描いて相関関係を調べています。これもさっそく Python で実施してみましょう。各変数ごとの相関関係をまとめて調べるには散布図行列を描くのが手っ取り早いです。
from pandas.tools.plotting import scatter_matrix
plt.figure()
scatter_matrix(data)
plt.savefig("image.png")
相関係数を求める
相関係数は共分散を二変数の標準偏差で割れば良いのですが pandas を使うと関数ひとつで簡単に求まります。
data.corr()
# =>
# X Y Z
# X 1.000000 0.300076 0.550160
# Y 0.300076 1.000000 -0.545455
# Z 0.550160 -0.545455 1.000000
5 ページ目にある相関行列を一発で求めることができました。だいたい一般的な目安としては 0.7 以上だと強い相関があると言われますから、元記事の記述の通り、微妙な相関関係だと言えるでしょう。
回帰分析をする
最後に 4 ページ目の最後に登場する回帰式を求めます。これは SciPy の統計関数のひとつ scipy.stats.linregress を利用して単回帰分析することで求まります。
# 値を取り出す
x = data.ix[:,0].values
y = data.ix[:,1].values
z = data.ix[:,2].values
# X と Z の回帰式
slope, intercept, r_value, p_value, std_err = sp.stats.linregress(x, z)
print(slope, intercept, r_value)
# => 0.108067677706 94.113690292 0.550160142939
# Y と Z の回帰式
slope, intercept, r_value, p_value, std_err = sp.stats.linregress(y, z)
print(slope, intercept, r_value)
# => -0.308556149733 96.0695187166 -0.545455364632
なお slope は傾き、 intercept は切片、 r_value は相関係数です。傾きを a 、切片を b として y = ax + b という一次式が求まります。
たとえば X と Z の一次回帰式なら y = 0.11x + 94.11 (小数点第 2 位まで) という式に回帰するというわけです。
まとめ
Python を使うとエクセルよりもさらに簡単に統計分析をおこなうことができました。二変数間の相関を調べるのは統計の基礎中の基礎ですから現実の問題にも応用するケースが多いですし、慣れると非常に短時間でこれらの分析をおこなうことができるようになります。