はじめに

今回も始まりました。やってみよう分析！シリーズ

今回は メトロポリス法と呼ばれるモンテカルロシミュレーションの手法を紹介します。点列をサンプリングするときに使う手法で、確率/統計モデルをシミュレーションする場合に使われます。ここではメトロポリス法の具体例として、物理学の 2次元イジングモデルシミュレーションをExcel VBAコードと共に取り上げます。

メトロポリス法

メトロポリス法のアルゴリズムを書き表すと次のようになります。

ある事象 $x$ の実現する確率が $p(x)$ で表されるとき、次の事象 $x'$ が発生する確率を $p(x')$ とします。このとき下記の条件で $x'$ の状態に移るか現在の状態 $x$ を維持するか決めます。

$p(x') \geq p(x_{t})$ ならば $x_{t+1} = x'$
$p(x') < p(x_{t})$ ならば確率 $r$ で $x_{t+1} = x'$、確率 $1-r$ で $x_{t+1} = x_{t}$
$r = p(x')/p(x_{t})$

メトロポリス法が伝えていることは、 確率が増える事象は必ず選択し、確率が減少する事象は確率 $r$ で選択、確率 $1-r$ で現状を維持するということです。

2次元イジングモデル

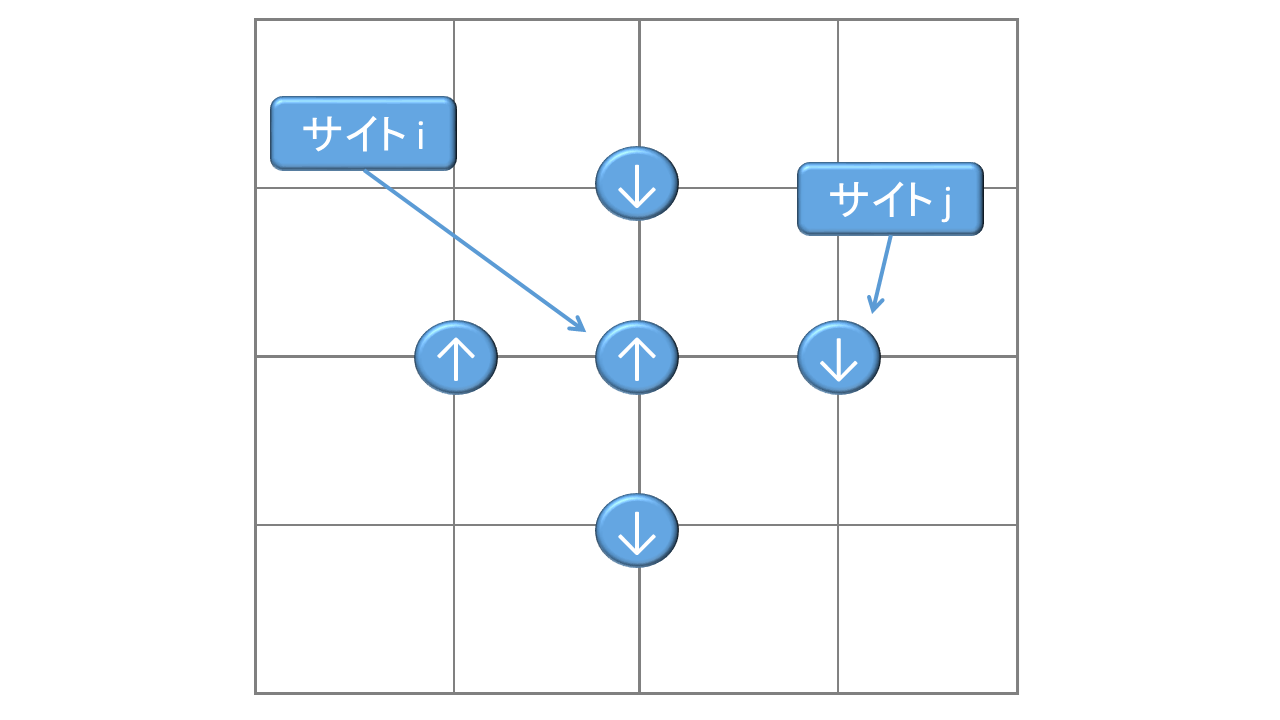
2次元イジングモデルは磁性体を記述するモデルの一つです。金属を冷やしていくと自発的に磁化が出現する場合があります。このようなケースを説明するのがイジングモデルです。2次元イジングモデルは2次元の格子状の空間上の各サイトに原子が乗っている状況を考えます。原子は スピンと呼ばれる量を持つとし、更にスピンは次のように上向き下向きの2つの状態を持つとします。

s_{i} =
\begin{cases}
+1 \qquad (\text{スピン上向き})  \\
-1 \qquad (\text{スピン下向き})
\end{cases}

二次元イジングモデルでは原子間のスピンの相互作用から生じるエネルギーを考えます。このとき、相互作用は隣接格子点のみ考えます。サイト $i$ とサイト $j$ の隣接格子の組を $<i,j>$ で表すと、スピン間の相互作用のエネルギーは下記で表されます($J$ は相互作用の強さ)。

E = - J \sum_{<i,j>} s _{i} s _{j}

スピンは上向き下向きの2つの状態しか持っていないので、向きを逆転したスピン $\bar s_{i}$ に対して下記の条件が成り立ちます。

\bar{s}_{i} = -s_{i}

このことを考慮すると、サイト $i$ におけるエネルギー $E_{i}$ とサイト $i$ のスピンを逆転させた時のエネルギー $\bar E_{i}$ は次のようになります($k(i)$ はサイト $i$ に隣接する
サイトを表しています)。

\begin{align}
E_{i} &= -J s_{i} \sum_{k(i)} s_{k(i)} \\
\bar{E}_{i} &=  -J \bar{s}_{i} \sum_{k(i)} s_{k(i)} = J s_{i} \sum_{k(i)} s_{k(i)}
\end{align}

このエネルギー$E_{i}$が実現するスピンの状態が出現する確率は

p_{i} \propto \exp(- E_{i} /T)

で与えられることが知られています。このとき

r= \exp(-(\bar{E}_{i} - E_{i} ) / T) = \exp(-(\varDelta E ) / T) = \exp(-2\bar{E}_{i} / T)

したがって $E<0$ のスピン配位の実現確率が高くなります。

2次元イジングモデルのメトロポリス法

それでは早速2次元イジングモデルのシミュレーションのためにメトロポリス法を適用してみます。
アルゴリズムは次のようになります。

初期のスピン配位を用意する（ランダムにスピン上下を各サイト上に割り当てる）。
ランダムにあるサイト$i$を抽出。
サイト$i$のスピンを反転させる $\bar{s}_{i} = -s _{i}$。
$ r = \exp(-2 \bar{E} _{i} / T ) $ を計算する ( $\bar{E} _{i} = J s _{i} \sum _{k(i)} s _{k(i)} )$。
$\varDelta E _{i} = \bar{E} _{i} - E _{i} = 2 \bar E _{i} > 0$ のとき、$[0,1]$の間の一様乱数 $\text{Rnd}$ を生成し、$\text{Rnd} < r $ならば、次の状態として $\bar{s} _{i}$ をとる。それ以外なら以前の状態を保つ。
$\varDelta E _{i} \leq 0$のときは次の状態として $\bar{s} _{i}$をとる。

このアルゴリズムをExcel VBA で実装した例が下記となります。実行するとセル上にスピンの上向き下向きの状態が色で表示されます。上向きが赤で表されます。

Const L = 100   '正方格子の大きさ
Const T = 1 '温度パラメータ
Const K = 200000   '計算回数
Const g = 1 'スピン間の相互作用の強さ
Dim spin(L, L) As Integer   'スピンの向きを入れる配列
Dim varCell As Range    'Rangeオブジェクト用

'セルの大きさを正方格子になるように調整
Sub CellConditions(x As Integer)
    'セルの高さと幅を初期状態に戻す
    Range(Cells(1, 1), Cells(x, x)).RowHeight = 13.5
    Range(Cells(1, 1), Cells(x, x)).ColumnWidth = 8.38
    '色をクリア
    Cells.Clear
    'セルの高さと幅を調整
    Range(Cells(1, 1), Cells(x, x)).RowHeight = 2
    Range(Cells(1, 1), Cells(x, x)).ColumnWidth = 0.15
End Sub

'初期配色（スピンの初期配位）
'画面表示なしで一度配列にデータを格納する(高速表示のため)。
Sub initialSpins(x As Integer)
    Application.ScreenUpdating = False
        For I = 0 To L - 1
            For J = 0 To L - 1
                If Rnd < 0.5 Then
                    spin(I, J) = 1
                    varCell(J + 1, I + 1).Interior.Color = RGB(220, 25, 1)
                Else
                    spin(I, J) = -1
                    varCell(J + 1, I + 1).Interior.Color = RGB(255, 255, 202)
                End If
            Next J
        Next I
    Application.ScreenUpdating = True
End Sub

'エネルギーの変分を計算
Function diffEnergy(x As Integer, y As Integer, z As Integer, g As Double) As Double
    Dim E As Double

    E = -g * spin(x, y) * _
            (spin(IIf(x - 1 > 0, x - 1, z - 1), y) _
                + spin(IIf(x + 1 < z, x + 1, 0), y) _
                + spin(x, IIf(y + 1 < z, y + 1, 0)) _
                + spin(x, IIf(y - 1 > 0, y - 1, z - 1)) _
            )

    diffEnergy = E
End Function

'メイン
Sub Ising()
    'セルの初期化
    CellConditions (L)

    'Rangeオブジェクト生成
    Set varCell = Range(Cells(1, 1), Cells(L, L))

    'スピンの初期配位をspin配列への保存し、varCellに対応する配色を保存。
    Randomize
    initialSpins (L)

    'varCellに保存したデータをセル行に表示。
    Range(Cells(1, 1), Cells(L, L)) = varCell
    Set varCell = Nothing

    For I = 0 To K
        Dim x As Integer
        Dim y As Integer
        Dim E As Double
        Dim r As Double

        'ランダムにサイトを抽出
        Randomize
        x = Int(Rnd * L)
        y = Int(Rnd * L)

        'スピンを反転させる
        spin(x, y) = -1 * spin(x, y)

        'エネルギーと確率の比率を評価
        E = diffEnergy(x, y, L, g)
        r = Exp(2 * ((-E) / T))

        'スピン状態の選択
        If E > 0 Then
            If Rnd < r Then
                spin(x, y) = 1 * spin(x, y)
            Else
                spin(x, y) = -1 * spin(x, y)
            End If
        Else
            spin(x, y) = 1 * spin(x, y)
        End If

        '配色
        If spin(x, y) = 1 Then
            Cells(y + 1, x + 1).Interior.Color = RGB(220, 25, 1)
        Else
            Cells(y + 1, x + 1).Interior.Color = RGB(255, 255, 202)
        End If
    DoEvents
    Next I
End Sub

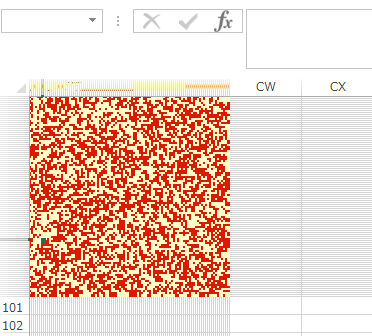
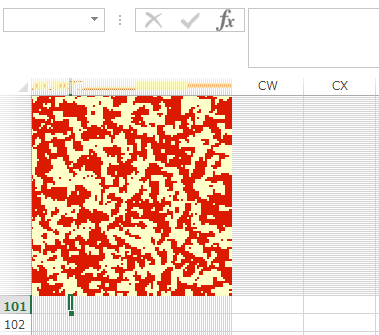
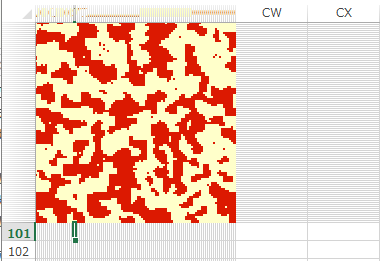
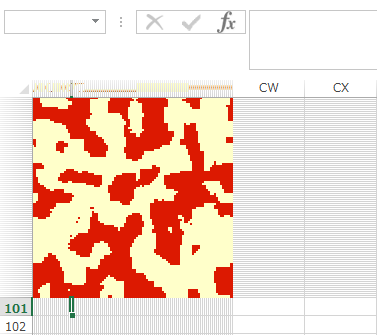
出力結果

下記の図は時系列で出力画像を並べたものです。最初はランダムにスピンのの上下が各サイト上に配置されます(磁化していない状態)。時間が経過するとスピン間の相互作用により、スピンが上向きと下向きの領域(磁化)ができてくる様子がわかります。温度パラメータを上げるとこのようなクラスターができにくくなります(この簡易実装ではパラメータを上げ過ぎたり下げ過ぎたりすると指数関数が発散するのでご注意ください)。