目次
このページを理解するのに必要な知識
余弦定理とは
余弦定理を使うと、2辺の長さと、その間の角度がわかれば、もう1辺の長さを出すことができます。
三角形の合同条件・決定条件
三角形というのは、3つの条件がそろえば、三角形の形が決定するようになっています。
下記のいずれかの条件がそろえば、三角形の残りの情報を導き出すことができます。
1. 3辺の長さ a,b,c が与えられた場合
2. 二辺の長さ b,c とその間の角 A が与えられた場合
3. 一辺の長さ a とその両端の角 B,C が与えられた場合
余弦定理とは、三角形のこの性質を表した定理です。
参考:三角形の決定条件と自由度
三平方の定理のおさらい
余弦定理を理解するためには、三平方の定理を理解している必要があるので、まずおさらいをします。
三平方の定理についてはコチラを参照
出典:http://www.geisya.or.jp/~mwm48961/kou2/cos_rule.htm
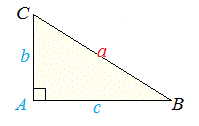
上図のような直角三角形があるとき、三平方の定理によって下記が成り立ちます。
a^2 = b^2 + c^2
では、直角三角形以外の場合は、どうでしょうか?
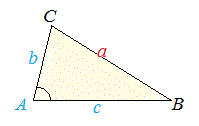
∠Aが90度より小さい場合
出典:http://www.geisya.or.jp/~mwm48961/kou2/cos_rule.htm
a辺の長さは、直角三角形だったときよりも短くなるはずです。
つまり、
a^2 = b^2 + c^2 - x
ということになります。
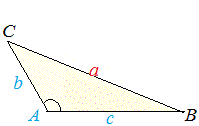
∠Aが90度より大きい場合
出典:http://www.geisya.or.jp/~mwm48961/kou2/cos_rule.htm
a辺の長さは、直角三角形だったときよりも長くなるはずです。
つまり、
a^2 = b^2 + c^2 + x
ということになります。
余弦定理を覚えると、このxの部分の式がわかり、直角三角形以外でも、aの長さを求めることができるようになります。
余弦定理
では、本題の余弦定理です。

出典:http://www.geisya.or.jp/~mwm48961/kou2/cos_rule.htm
上図のような三角形があるとき、余弦定理によって、下記の式が成り立ちます。
b,cの長さと、Aの角度がわかれば、aの長さを求めることができます。
他の辺に関しても、2辺の長さとその間の角度がわかれば、もう1辺の長さが導き出せます。
a^2 = b^2 + c^2 − 2bc・cos∠A
b^2 = c^2 + a^2 − 2ca・cos∠B
c^2 = a^2 + b^2 − 2ab・cos∠C
下記は、角度を求める場合の方程式。上記の式を変形させたもの。
cos∠A = b^2 + c^2 - a^2 / 2bc
cos∠B = a^2 + c^2 - b^2 / 2ac
cos∠C = b^2 + a^2 - c^2 / 2ac
余弦定理の証明
なぜ、余弦定理が成り立つのか、三角関数、三平方の定理を利用して証明します。
出典:http://www.geisya.or.jp/~mwm48961/kou2/cos_rule.htm
証明の仕方
-
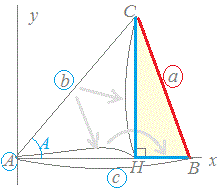
上記の図のように、CからHへABと90°に交わる直線を引く。
こうすると、CAHとCHBの2つの直角三角形ができる。 -
このとき、CHの長さは、三角関数のsinAの方程式で出せる。
AHの長さも、三角関数のcosAを使って求められる。
HBの長さは、c - AHで求められる。
# CHの長さを出す
sinA = CH / b
CH = b x sinA
# AHの長さを出す
cosA = AH / b
AH = b x cosA
# HBの長さを出す
HB = c- AH
- これで、右側の直角三角形の2辺である、CHとHBの長さがわかったので、aの長さは、
三平方の定理を用いて出すことができる。
a^2 = CH^2 + HB^2
= b・sin^2A + (c - b・cosA)^2
= b^2・sin^2A + (c - b・cosA)・(c - b ・ cosA)
= b^2・sin^2A + (c^2 - c・b・cosA - c・b・cosA + b^2・cos^2A)
= b^2・sin^2A + c^2 - 2cb・cosA + b^2・cos^2A
= b^2・(sin^2A + cos^2A) + c^2 − 2bccosA
∴ a^2 = b^2 + c^2 − 2bc・cosA
∴とは「結論」を意味する数学の記号。
例題
b,cの長さ Aの角度がわかっているとき、aの長さは、下記の方法で導き出せます。
b=5, c=3 , ∠A=60°
cos60°の値は1/2になります。
これは三角比といって、決まった値です。
三角比についてはコチラを参照
a^2 = b^2 + c^2 − 2bc・cosA
a^2 = 5^2 + 3^2 - 2・5・3・cos60°
a^2 = 49
以上
[参考]
http://www.geisya.or.jp/~mwm48961/kou2/cos_rule.htm
[関連記事]
プログラマーのための数学 - 目次