目次
三角関数 sinθ,cosθ,tanθ
三角関数というのは、sin(サイン)、cos(コサイン)、tan(タンジェント)とかのことです。
どういう時に使うのかというと、直角三角形の2辺の長さと角度が与えられた時、残りの辺の長さを求めるためなどに利用します。
一言で言うと・・・
cosθ(コサイン)というのは、座標におけるx座標、
sinθ(サイン)というのは、y座標のことです。
とりあえず、下記の方程式をとにかく覚えてください!
出典:http://alg.cias.osakafu-u.ac.jp/webMathematica/HighSchool/tri_ratio/theme0.jsp
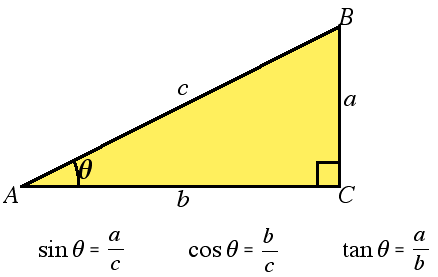
上図のような直角三角形があるとき、下記の方程式が成り立ちます。
sinθ = a / c
cosθ = b / c
tanθ = a / b
この方程式が成り立つのは、下記の条件の時だけです。
∠C = 90° 且つ 0°<θ<90°
∠Cが90°であり、θが0°以上90°以下であること、
つまり、直角三角形の場合のみ成り立ちます。
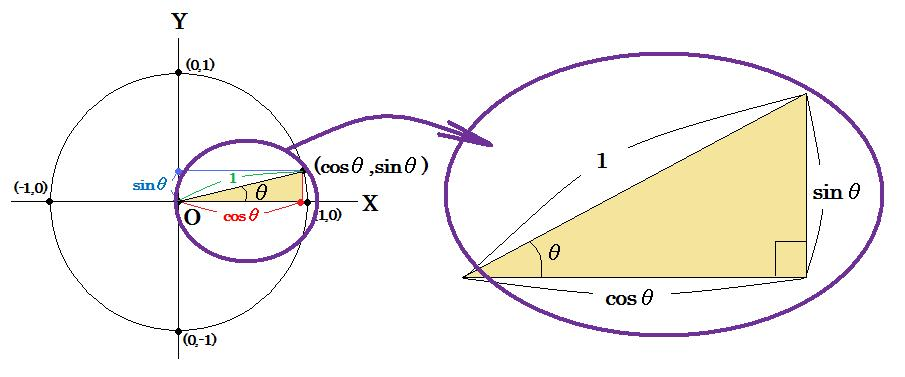
単位円を用いて三角関数を理解する

出典:進研ゼミ
上記の図のように、
単位円(半径1の円)の原点(円の中心)から引いた線の、x軸から原点方向への角度をθとしたとき、
点Pの座標 = (cosθ, sinθ)
sinθ = (点Pのy座標)
cosθ = (点Pのx座標)
となります。
つまり、こういこうことです。
繰り返しになりますが、
cosθ(コサイン)というのは、座標におけるx座標、
sinθ(サイン)というのは、y座標のことです。
上図のように、(cosθ, sinθ)という座標になります。
よって、x,yの座標を求める方程式は、下記ということになります。
xの座標 = sinθ = a / c
yの座標 = cosθ = b / c
この方程式は、余弦定理の話で、大活躍します。
以上
参考:
公式不要!単位円を使ったcos,sin,tanの簡単理解
高校生の苦手解決Q&A
[関連記事]
プログラマーのための数学 - 目次