非階層型クラスタリング k-means
それでは、機械学習やその他色々について得た知識を
復習and記事作成の練習and個人の備忘録としてまとめていきます！
前回、"階層型クラスタリング"について書いたので、
今回はそれと対になる、"非階層型クラスタリング"について書いていこうと思います！
⚠︎※※注意※※⚠︎
・出来るだけ専門知識のあまりない人に対して、分かりやすく書くことを目標にしています。
そのため、厳密に言うと間違っている部分があると思いますがご容赦ください。
・また、ネットで調べたレベルの知識がほとんどなので、
"厳密に言うと"レベルではなく間違っている箇所があるかもしれません。。
その場合は非常に申し訳ないです。指摘していただけると幸いです！
前回までの記事
・機械学習について
・教師あり学習 〜回帰〜
・教師あり学習 〜分類〜
・Random Forest
・階層型クラスタリング
クラスタリング
教師なし学習の、クラスタリングということについて少しだけおさらいをしたいと思います。
(前回のコピペです、すみません。。)
クラスタリングとは
空間にバラバラな点として存在するデータを
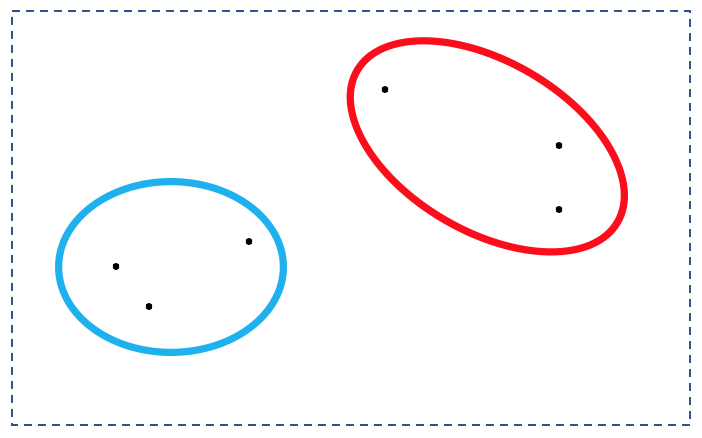
図のように、何らかの基準で「似たもの」を集めるという技術です。
クラスタリングの手法には、大きく分けて二種類あり、
"階層型クラスタリング"と"非階層型クラスタリング"が存在します。
今回は"非階層型クラスタリング"の代表的な手法である、k-meansについて書いていきます。
k-means
非階層型クラスタリングでは、階層型クラスタリングと違って、
先に、データをいくつのクラスターに分けるかを指定しなければなりません。
今回のk-meansでは、2つのクラスターに分けていきたいと思います。
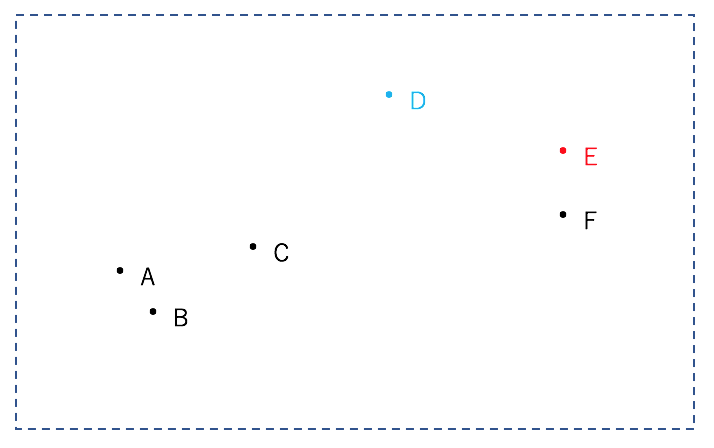
まず初めに、基準となる２つの点をランダムに選択します。
今回はDとEが選択されたとします。
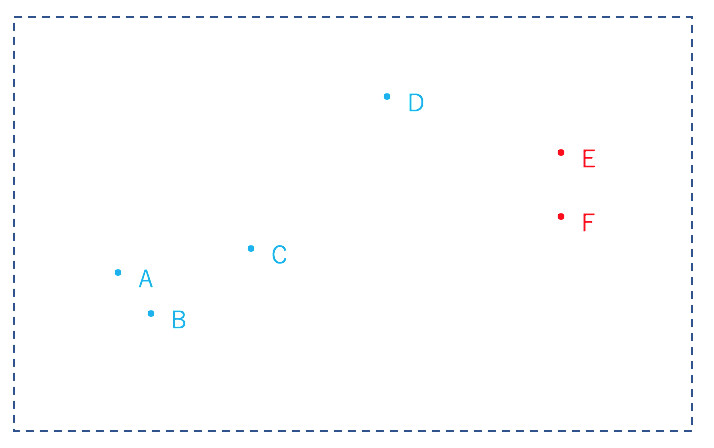
そして、残りの点を"基準点のどちらに近いか"で分けます。
次に、分けられたクラスター内の重心を計算します。
(大体の雰囲気で重心を決めたのでズレていますが、そこはツッコんではいけません。笑)
今度はこの重心を基準として、同様に残りの点を"基準点のどちらに近いか"で分けます。
そしてまた、クラスター内の重心を計算します。
もう一度この重心を基準として、同様に残りの点を"基準点のどちらに近いか"で分けます。
今回はこの段階でクラスターの変動がなくなり、安定した状態となりました。
このように、
- 全ての点において、基準点との距離を計算し、近い方の基準点と同じクラスターとする。
- クラスター内の重心を取り、次の基準点とする。
というのを重心が変動しなくなるまで繰り返すことによってクラスタリングを行うのが、"k-means"です。
階層型クラスタリングに比べて、計算量が非常に少ないのが特徴となっています。
初期値依存性
k-meansは、非常に初期値（最初に選択される基準点）に依存します。
下の図を二つのクラスターにクラスタリングしてみましょう。
「こんなもの右上と左下に簡単に分類できるやろ！」
と思いきや、、
例えば一番右上の二点が初期基準点となってしまうと・・
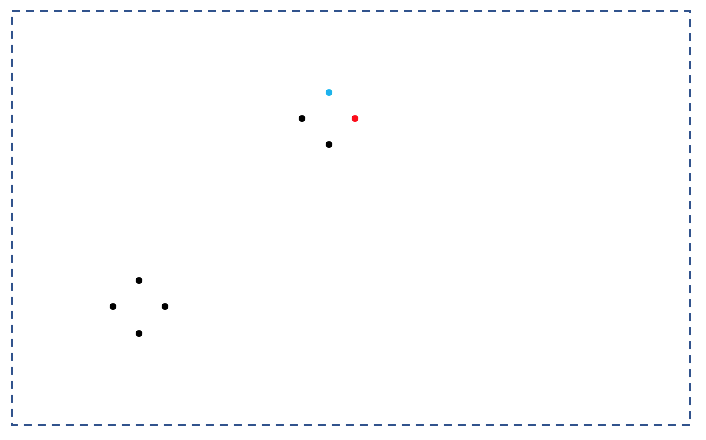
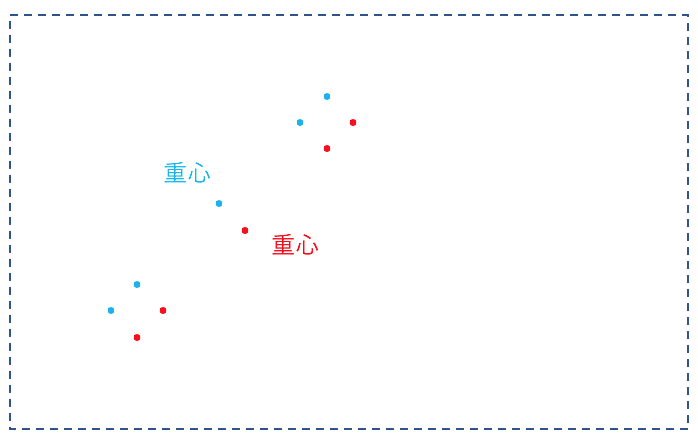
のようになり、この状態で安定してしまいます。
こうならないために、k-meansを行うときは、
"複数回行なった上で、クラスター内平均距離が最小となる初期値を選択する。"
などの工程が必要となります。
まとめ
・非階層型クラスタリングには、代表的な手法として"k-means"が存在する。
・k-meansでは、
①基準点を元にクラスターに分ける
②クラスターの重心を新たな基準点とする
を繰り返すことでクラスタリングを行う。
・クラスタリングの結果は、初期値に非常に依存してしまう。そのため、複数回行なってクラスター内平均距離が最小となる初期値を選択する、などを行う必要がある。
・メリットとしては階層型クラスタリングに比べて計算量が非常に少ない。
・デメリットとしては、上記の初期値依存性の他、クラスタリングを行う段階で分割数を決めなけばならない、などがある。
あとがき
k-meansの初期値依存性は、初めて図で見た時「なるほどー！おもしろいなぁ」と思った記憶があります。
やっぱり可視化することは、理解する上でかなり重要ですね。
情報の共有にも使えますし！
ここまで読んでいただき、ありがとうございました！