階層型クラスタリング

いえーい、機械学習やその他色々について得た知識を
復習and記事作成の練習and個人の備忘録としてまとめていくぜーい！

今回は、教師なし学習の"クラスタリング"の手法の一つ、
"階層型クラスタリング"について書いていくぜーい！

⚠︎※※注意※※⚠︎

・出来るだけ専門知識のあまりない人に対して、分かりやすく書くことを目標にしています。
　そのため、厳密に言うと間違っている部分があると思いますがご容赦ください。

・また、ネットで調べたレベルの知識がほとんどなので、
　"厳密に言うと"レベルではなく間違っている箇所があるかもしれません。。
　その場合は非常に申し訳ないです。指摘していただけると幸いです！

前回までの記事

・機械学習について
・教師あり学習　〜回帰〜
・教師あり学習　〜分類〜
・Random Forest

クラスタリング

教師なし学習の、クラスタリングということについて少しだけおさらいをしたいと思います。

クラスタリングとは

空間にバラバラな点として存在するデータを

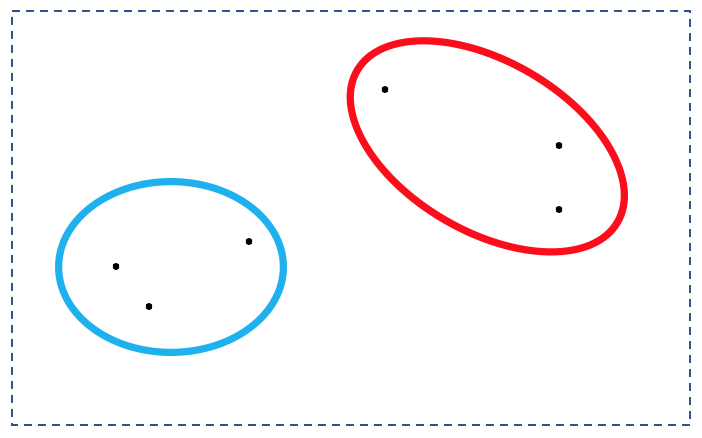
図のように、何らかの基準で「似たもの」を集めるという技術です。

クラスタリングの手法には、大きく分けて二種類あり、
"階層型クラスタリング"と"非階層型クラスタリング"が存在します。

今回は"階層型クラスタリング"について説明していきます。

手順

階層型クラスタリングはすごく単純で、
近いもの同士をくっつけていって、最終的に全てのデータを一つにまとめていきます。

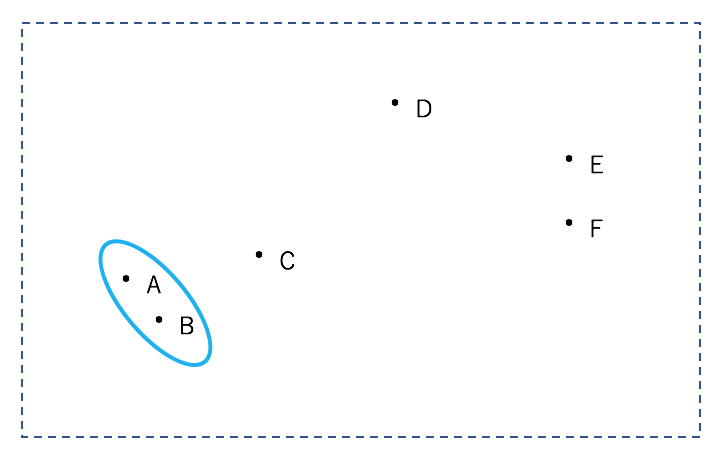
先ほどのデータで階層型クラスタリングを行なっていきましょう。

分かりやすくするため、点にはA~Fという名前をつけています。
まず、全ての点の組み合わせにおいて距離を計算し、一番近いもの同士を一つのクラスターとします。
今回の場合は、AとBが一つのクラスターとなります。

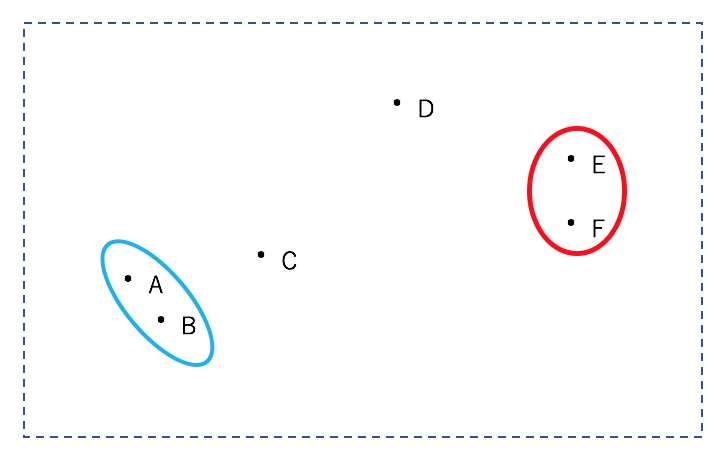
次に、ABを一つの点とみなし、同様に5つの点の全ての組み合わせにおいて、一番近いものどうしを一つのクラスターします。

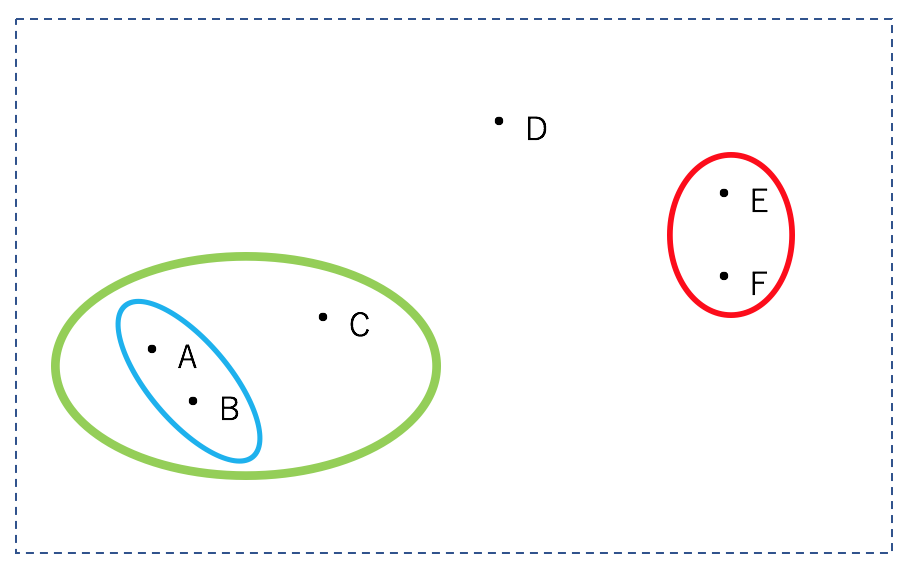
全ての点が同じクラスターになるまで繰り返します。

これらの過程を、デンドログラム(樹形図)で表すと次のようになります。

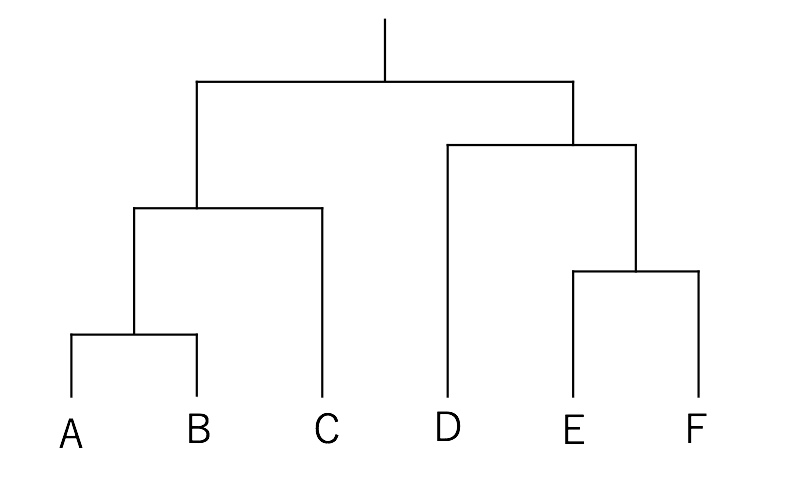
これを上から順に辿り、
２つの分ける必要があればABCとDEF
3つに分ける必要があればABCとDとEF・・

のように、目的に応じて好きな数に分類すればよい、という分けです。

階層型クラスタリングのメリットとしては、

・好きな数に分けることができる。
・試行ごとに結果が常に一定。

などがあります。

デメリットとしては、全ての点の組み合わせを逐一計算しなければならないがゆえの

・計算量の多さ

が浮かび上がります。
ビッグデータと呼ばれるデータを解析していく上では、このデメリットが致命的だったりすることもあります。

距離の計算方法

上記の手順の説明では、単純に「距離を計算する」と言いましたが、
距離の計算方法にはいくつかあります。

最短距離法

各クラスターにおいて、一番近い点同士の距離を、"クラスターの距離"とする方法。

最長距離法

各クラスターにおいて、一番遠い点同士の距離を、"クラスターの距離"とする方法。

群平均法

クラスター同士の全ての点同士の距離の平均を、"クラスターの距離"とする方法。

ウォード法

あるクラスター同士が結合すると仮定した時、結合後の全てのクラスターにおいて、
クラスターの重心とクラスター内の各点の距離の二乗和の合計が最小となるように、クラスターを結合させていく方法。
計算量が非常に大きくなるが、分類感度が高い。

まとめ

・階層型クラスタリングは、全ての点同士の距離を計算し、近いものから順にくっつけていく方法である。

・メリットとして、計算後に好きなクラスター数にすることができる、試行ごとに結果が変わらない、などが挙げられる。

・デメリットとしては、計算量が非常に多い。

・クラスター同士の距離の計算方法は数パターン存在し、ウォード法は分類感度が高いが計算量が多い。

あとがき

階層型クラスタリングは、中々感覚的に掴みやすいのではないでしょうか？

クラスタリング自体がそもそも、使い所が難しい気がします。
クラスタリングしてみた結果、「このクラスターはどういうクラスターだろうか。。」とラベル（らしきもの）をつけることができないことも少なくないです。

ですが、うまく使いこなすと、人間では気づきにくい何か違った視点をもたらしてくれるかもしれないです。

使いこなせるようになれるといいなぁ。

ここまで読んでいただき、ありがとうございました！