Random Forest
いつも通り、機械学習やその他色々について得た知識を
復習and記事作成の練習and個人の備忘録としてまとめていきますよ!
今回は、前回説明した「教師あり学習 分類」のアルゴリズムの一つ、
"Random Forest"について書いていきたいと思います!
⚠︎※※注意※※⚠︎
・出来るだけ専門知識のあまりない人に対して、分かりやすく書くことを目標にしています。
そのため、厳密に言うと間違っている部分があると思いますがご容赦ください。
・また、ネットで調べたレベルの知識がほとんどなので、
"厳密に言うと"レベルではなく間違っている箇所があるかもしれません。。
その場合は非常に申し訳ないです。指摘していただけると幸いです!
参考サイト
【Hivemall入門】RandomForestで毒キノコ推定モデルを作る
前回までの記事
・機械学習について
・教師あり学習 〜回帰〜
・教師あり学習 〜分類〜
決定木
"Random Forest"の"Forest"は、そのままの意味で"森"を表します。
"森"ということは、"木"の集まりなわけです。
その"木"が"決定木"と呼ばれるものです。
まずはこの決定木について説明します!

[決定木 wikipediaより]
従属変数=目的変数 です。
画像では、ゴルフをするかしないかを予測する時の決定木になっていますね。
(上司の気まぐれでゴルフをするかどうかが決まるので予測したい、とかでしょうか?笑)
今までゴルフが開催された日のデータを、まずは天気という観点から見てみると、
例えばくもりの日には100%行われています。
なので、次の予定日の天気が曇りの場合、高い確率で開催されるであろうことが予測できます。
このように、予測したい目的変数に対して、説明変数一つの観点から見て分岐させていったものが"決定木"です。
ジニ係数
ではその分岐させる説明変数はどのようにして決めているのでしょうか?
先ほどの図でいくと、一番最初の分岐が"強風かどうか"では駄目だったのでしょうか?
また、湿度で分岐させる時"70%"というのはどのようにして決めたらいいのでしょうか?
それを決めるのが、"ジニ係数"と呼ばれるものです。
ジニ係数は格差を定量的に表すことの出来る値です。
所得格差を表す時によく使われるみたいですね。

このようなAさん〜Dさんがいるグループでは、月収が10万~57万まで存在するので、
所得格差は大きく、ジニ係数も大きくなります。
ですが、このグループを、
「AさんとBさん」、「CさんとDさん」というような、"30歳"を基準に二つのグループに分けると、
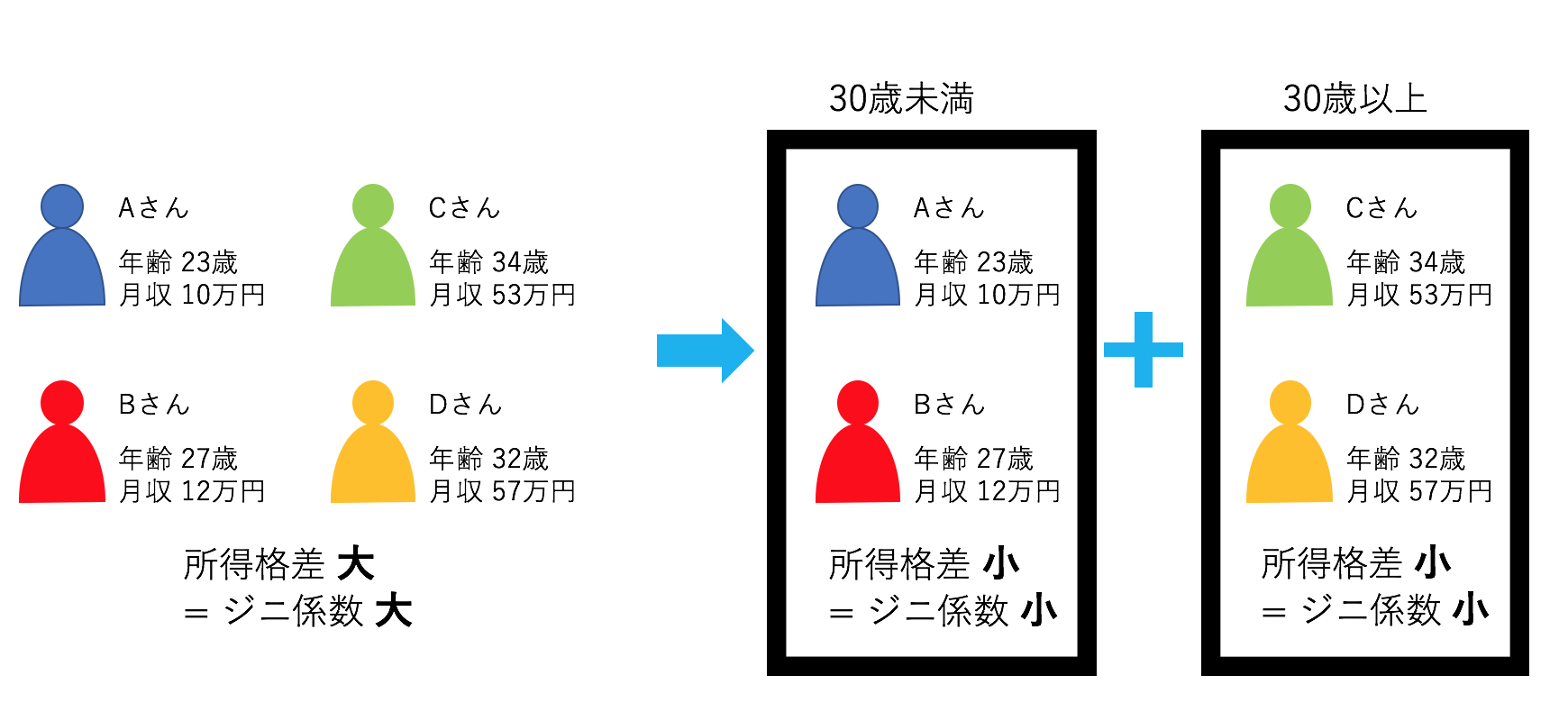
というように、ジニ係数が小さくなります。
決定木では、このように、格差が小さくなるような条件を取り出すことで作られます。
ジニ係数以外にも、エントロピーやカイ二乗統計量などが用いられることもあります。
アンサンブル
ジニ係数を元に、天気を第一分岐とする決定木が作られたわけですが、
もしかしたら、"前日が飲み会だったか"という変数で切られた決定木のほうが有効かもしれません。
"Random Forest"は "森"ということで、決定木は一つだけでなく大量に作られます。
そうしていくと、ある決定木では「ゴルフをする」という結論がなされ、
他の決定木では「ゴルフをしない」という結論がなされることもあるかもしれません。
その時に多数決をとって、予測を確定するのが"アンサンブル"という手法です。
100個決定木を作って70個が「ゴルフをする」という結論になったなら、
そのモデル全体での予測としては、「ゴルフをする」という予測になるわけです。
ランダムなサンプリング
ジニ係数とアンサンブルの話を聞いて、「おや?」と思った方がいるかもしれません。
「ジニ係数を元に決定木を作成するなら、何個決定木を作ろうとも同じ決定木が出来上がるのでは?」
その通りです。
同じデータと同じ条件で決定木を作っても意味はありません。
そこで使われるのがランダムなサンプリングです。
"Random Forest"の"Random"の部分ですね!
ここでのランダムなサンプリングには二種類あって、
・学習データから重複を許してN組のサンプル集合を抽出
・説明変数をM個の中からm個抽出
というものです。
そうして、多種多様なデータセットを作ることで、
違う決定木を大量に作ることができ、アンサンブルが効いてくる、というわけです。
まとめ
Random Forest とは
- 学習データから重複を許してランダムに複数組のサンプル集合を抽出
- 各組に対して説明変数もランダムに抽出
- ジニ係数を計算し、決定木を作成
- 予測時は各決定木の結果でアンサンブルに推定
となります!
あとがき
初めてアルゴリズムの中身を説明しましたがどうだったでしょうか??
分かりやすく書けているといいのですが、、説明って難しい。
次は教師なし学習について書きたいと思います。
ここまで読んでいただき、ありがとうございました!