1章 記述統計の基本と基本的な確率分布 〜1.1 確率関数と記述統計
※この投稿はシリーズものの一部です。
part5 <-[part0](http://qiita.com/yuusei/items/49a63f4402afc66243e6)->part7
注意)このエントリは下記の章立てたシリーズの最初の章のエントリとなります。
これらのエントリは数式を理解する為に絵が多く入っています。
ただし、当然数式も多く入っている為、あまり耐性のない方は無理をせず閉じていただければと思います。
1章 記述統計の基本と基本的な確率分布 (平均/分散/標準偏差/共変動と相関/一様分布/ガウス分布 etc…)
2章 推計統計の基本と対応する確率分布 (検定/推定/t分布/χ二乗分布/F分布 etc…)
3章 様々な確率分布 (二項分布/ポアソン分布/負の二項分布/対数正規分布/指数分布/アーラン分布/ガンマ分布 etc…)
4章 確率過程を理解する為の基礎概念 (確率空間/独立性/ルベーグ積分/大数の弱・強法則/フーリエ変換/中心極限定理 etc…)
5章 確率過程入門 (ウィーナー過程/レヴィ過程/ガウス過程/マルコフ過程/MCMC etc…)
6章 確率的最適化入門 (確率過程の入った待ち行列理論 / 確率的最適制御-動的計画法)
それでは始めます。
1章 記述統計の基本と基本的な確率分布
この章の目標は、平均や分散、標準偏差などを3次元までのレベルで絵を記載して理解できるようにするのが目標です。
著者の好みでわけのわからないこだわりが入る場合がありますが、なるべくわかりやすく書いていきたいと思います。
1.1 確率関数と記述統計
この節では、まず確率関数の定義を示し、続けてその定義を基にして、平均や分散、標準偏差や相関を絵にして
説明していきたいと思います。
1.1.1 確率関数(離散-連続)
1.1.2 同時確率(離散)
1.1.3 同時確率(連続)
同時確率を離散から連続にするとどうなるかという議論は、
二つほど前のエントリで書いたように、
根本的には「整数値の集合を対象にするか」か「連続値の集合を対象にするか」の違いだけです。
なので、今回やるべき事は必然的に「前回の離散式を連続の世界にお化粧をつけて移す」作業になります。
そんなわけで、大して大げさなことをやるわけではないので、
ちゃっちゃか行きましょう。
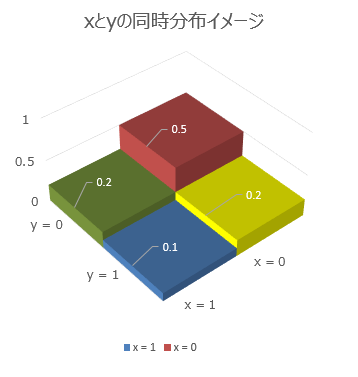
前回紹介した同時確率(離散)はこれでした
\begin{eqnarray}
{\rm P} (x, y) & \geq & 0 & , \\
\sum_{x \in \mathbb{Z}} \sum_{y \in \mathbb{Z}} {\rm P} (x, y) & = & 1 & .
\end{eqnarray}
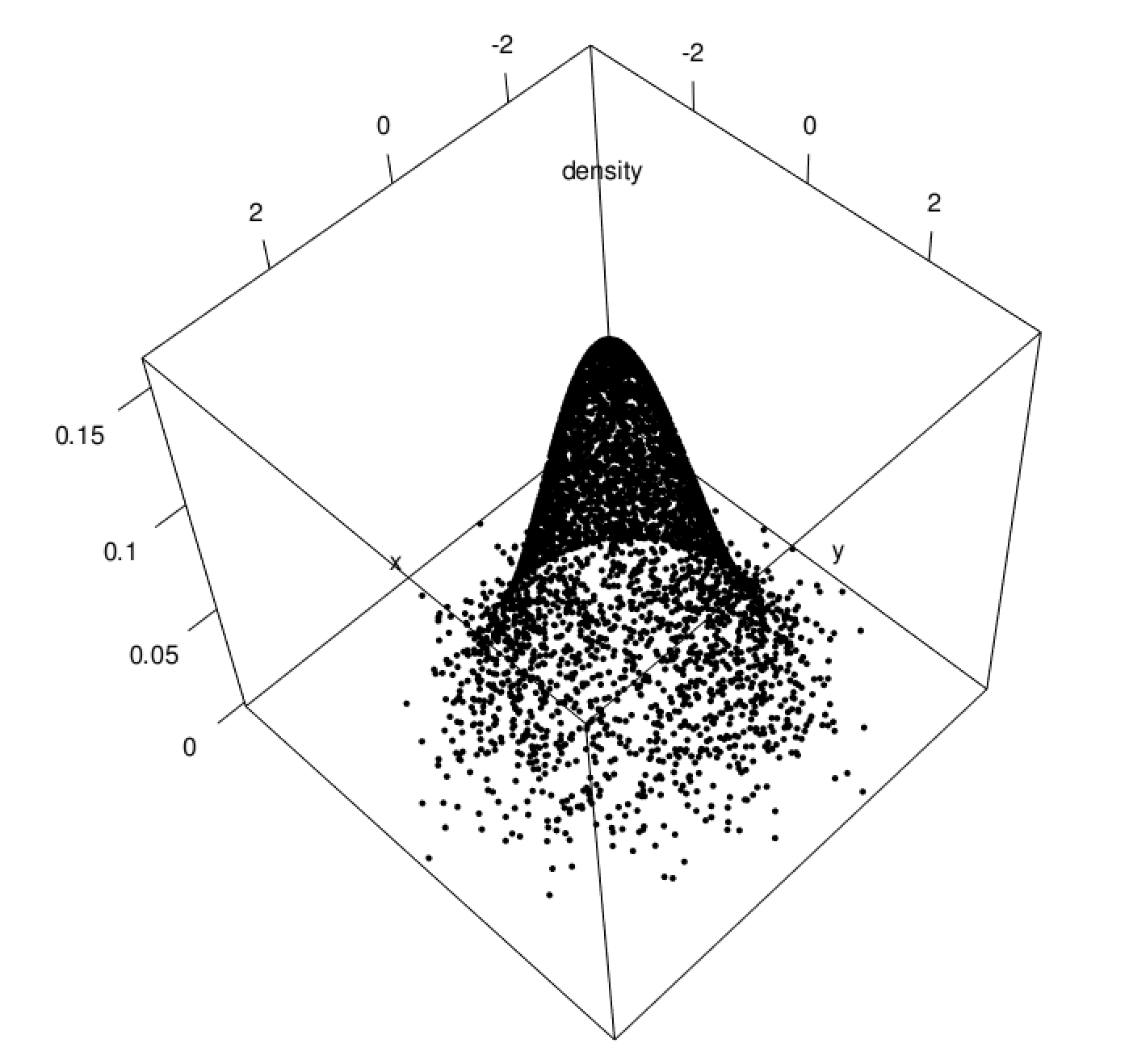
これを連続の世界に持っていくと、こうなります。
\begin{eqnarray}
p (x, y) & \geq & 0 & , \\
\int_{- \infty}^{\infty} \int_{- \infty}^{\infty} p (x, y) dx dy & = & 1 & .
\end{eqnarray}
高校で数学を学んでいる人には当たり前の光景ですかね。
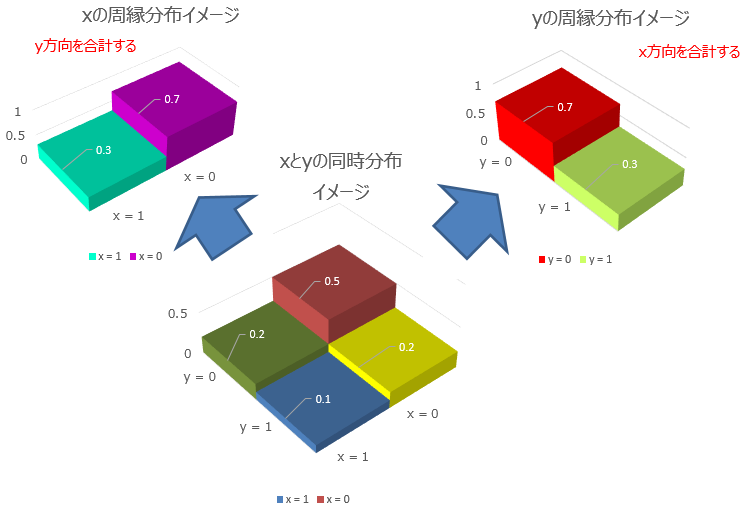
さて、いつも通り、イメージ図を置いて終わりにしましょうか。
これが離散
これが連続
これが離散の周縁分布も加えたバージョン
これが連続の周縁分布を加えたバージョン
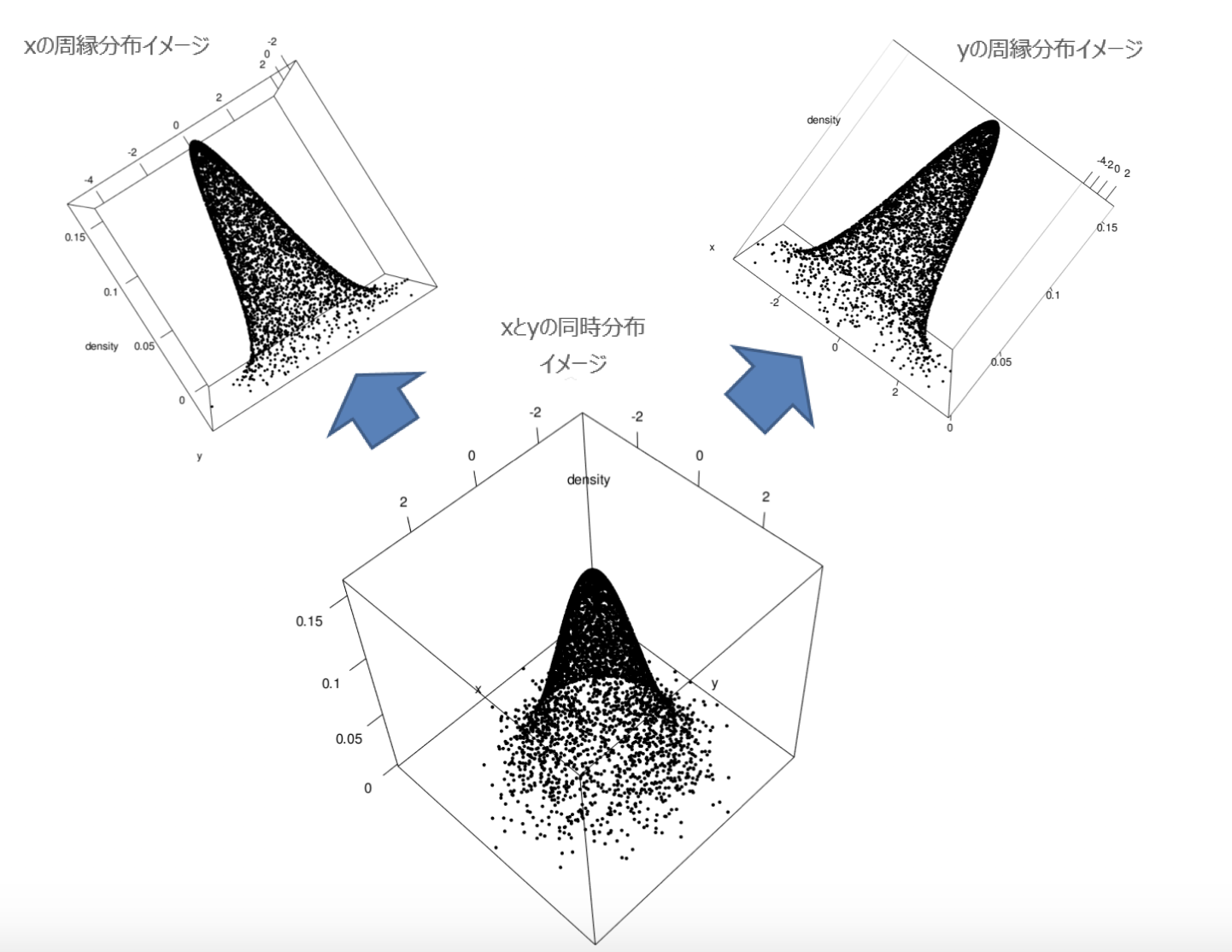
$ \sum $ が $ \int $になった以外特に印象の違いはないと思います。
(※まぁ、上の連続の方の周縁分布は、3dの図をグリグリ回して作っただけなので、周縁分布の定義から超絶外れてるんですけどね。
なので「周縁分布はあくまでもイメージです」)
3dの図を作成するコードはこことかこことかを見ていただければわかるので、そちらを参照してください(Rをインストールしておく必要があります)
この一連のエントリで使っているRコードは、一つの賞が終わるたびに、GitHubにでも乗せて公開しようと思います~~(使い方覚えなきゃ・・・)~~
これで連続バージョンが終わったので、
次回は やっと期待値と分散の話に入ります。
少し先回りして予告すると、
なぜ、統計の世界では「期待値を平均とも呼ぶのか」について話したいと思います。
これは、会社の同僚から割と反応の良かった説明なので、
学生の頃に、平均と期待値は別物として頭に刷り込まれている方、
ちょっと期待していてください。
次エントリ 1.1.4 期待値・平均と分散 (今月中投稿予定)