ゆっくりとデータサイエンティスト回りの概念/手法を整理してみようと思う part7
※この投稿はシリーズものの一部です。
part6 <-[part0](http://qiita.com/yuusei/items/49a63f4402afc66243e6)->part8
注意)このエントリは章立てたシリーズの最初の章のエントリとなります。
これらのエントリは数式を理解する為に絵が多く入っています。
ただし、当然数式も多く入っている為、あまり耐性のない方は無理をせず閉じていただければと思います。
1章 記述統計の基本と基本的な確率分布
この章の目標は、平均や分散、標準偏差などを3次元までのレベルで絵を記載して理解できるようにするのが目標です。
著者の好みでわけのわからないこだわりが入る場合がありますが、なるべくわかりやすく書いていきたいと思います。
1.1 確率関数と記述統計
この節では、まず確率関数の定義を示し、続けてその定義を基にして、平均や分散、標準偏差や相関を絵にして
説明していきたいと思います。
1.1.1 確率関数(離散-連続)
1.1.2 同時確率(離散)
1.1.3 同時確率(連続)
1.1.4 平均と標本分散と標本標準偏差(離散)
このエントリでは、平均と標本分散、標本標準偏差について視覚的なチャートも交えて説明していきたいと思います。
その為に、一つシチュエーションを設定します。
[シチュエーション]
袋の中に 1~40までの数字が入ったくじ引きがあるとして、
引いた数字 × 1,000円
を賞金とするゲームを設定します。
この時、結果がどれくらいバラついているかを、
数字で表現したいと思います。
なんでそんな事を知りたいかと言うと、
例えば、3人が同じくじを引くシチュエーションで、
7が出たAさん、
13が出たBさん、
25が出たCさん
がいたとします。三人の出目の平均は15になるわけですが、
平均から8も少ないAさん、
平均から2少ないBさん、
平均より10多いCさん、
がいるわけです。この時、Bさんの飽く無き好奇心が、
「Aさんの損は8,000円だけど、Cさんの得は10,000円だ。ではCさんの得はAさんに比べてどれくらい違うのかな?」
と囁きました。
気になりません?他の人が自分よりどれくらい得したか。
まぁ、気になる人も、気にならない人もいると思いますが、
この時、結果がどれくらいバラついているかがわかりると、
この損得感を数値化できます。
え?悪趣味?まぁいいじゃないですか。
平均や分散はビジネスでもよく使われてて、
それって結局は損得の世界が絡んでくるんですから。
必要悪だと思って、説明に入ります。
さて、今度は同じシチュエーションで9人がくじを引きました。
(視覚的にインパクトが強いので、人数を増やしています)
この時、9人の数字とその平均は以下のようになったとします。
| 引いた順番 | ラベル | 出目 |
|---|---|---|
| 1人目 | $x_1$ | 22 |
| 2人目 | $_2$ | 21 |
| 3人目 | $x_3$ | 23 |
| 4人目 | $x_4$ | 11 |
| 5人目 | $x_5$ | 16 |
| 6人目 | $x_6$ | 34 |
| 7人目 | $x_7$ | 18 |
| 8人目 | $x_8$ | 14 |
| 9人目 | $x_9$ | 21 |
| 平均 | $\bar{x}$ | 20 |
平均値 $\bar{x}$ は、各出目の大きさを全部足して、
個数で割ったものになるわけで、
すなわち
\bar{x} = \frac{1}{9} \sum_{i = 1}^{9} x_i = \frac{1}{9}(22+21+23+11+16+34+18+14+21) .
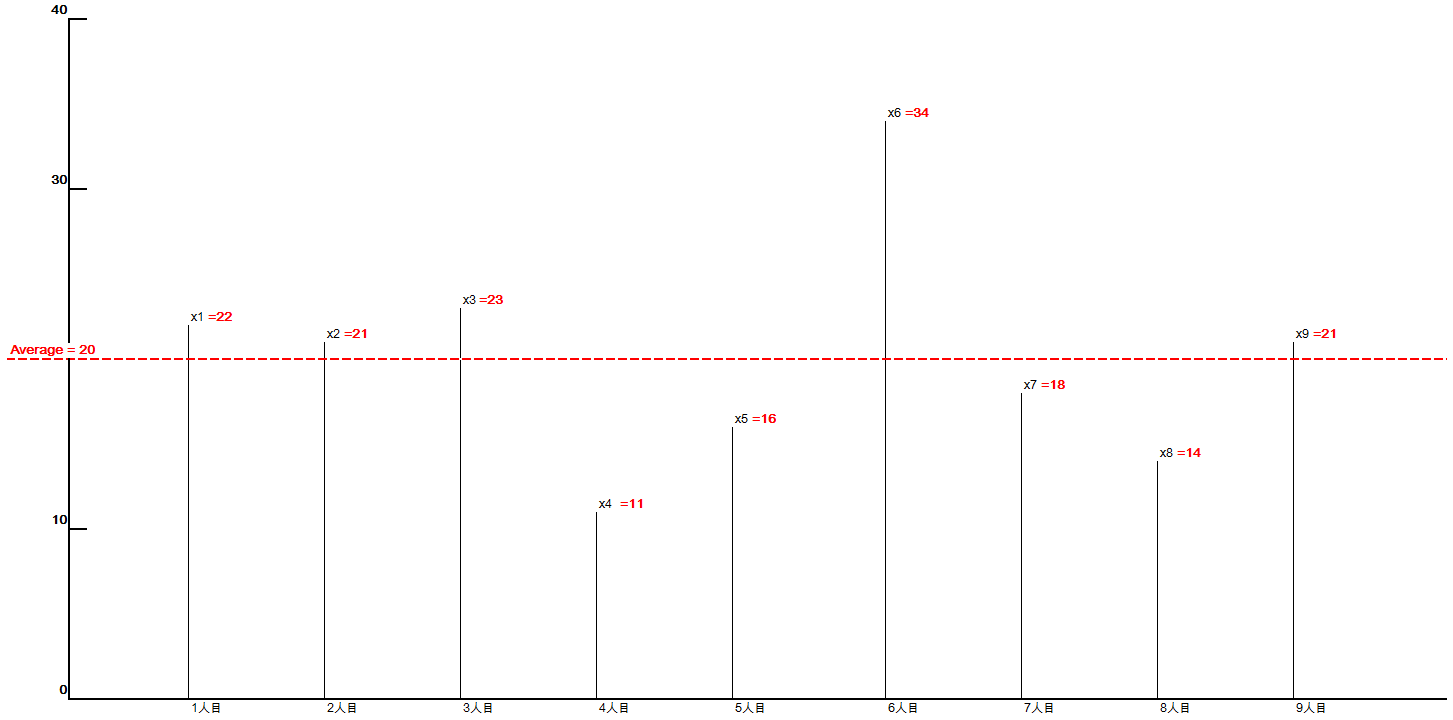
さて、上の表を絵に落としてみましょう。
横軸が引いた順番、縦軸が出目になります。
垂直に伸びている棒が出目の大きさを表しており、
長いほど出目が大きいと言う事になります。
となります。
平均がわかったので、分散(標本分散と不偏分散)が求められます。
まず、標本分散 $s^2$ の一般的な式を確認しておきましょう。
上の式が一般的な式、下の式が今回の場合です。
s^2 = \frac{1}{n} \sum_{i = 1}^{n} (x_i - \bar{x})^2 \\
s^2 = \frac{1}{9} \sum_{i = 1}^{9} (x_i - \bar{x})^2
式については特に説明は不要ですかね。
ここで、恐らく誰もが $ (x_i - \bar{x})^2 $ の部分を理解するのに、
難儀したのではないかと思います。
この部分は「平均からの差を取って、二乗する」と言う作業になるわけですが、
「なぜ二乗せねばいかんのか???」この事が腹落ちせず、
統計や確率の勉強が嫌になった人もいると思います。
なので、そこを説明しきれなければ凡百の記事/参考書と変わらないと思うので、
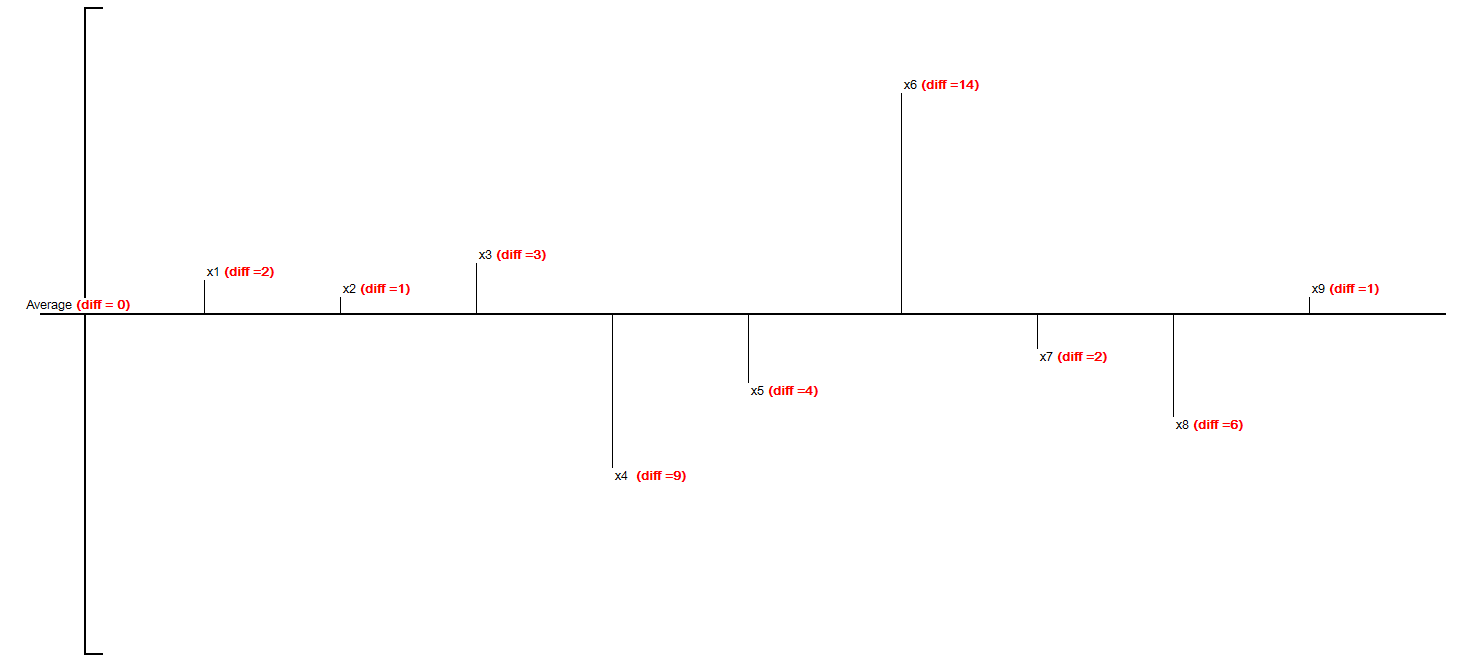
理解して貰う為に先ほどの図に少し手を入れましょう。
こうして・・・
こう!
というわけで、わかっていただけたでしょうか?
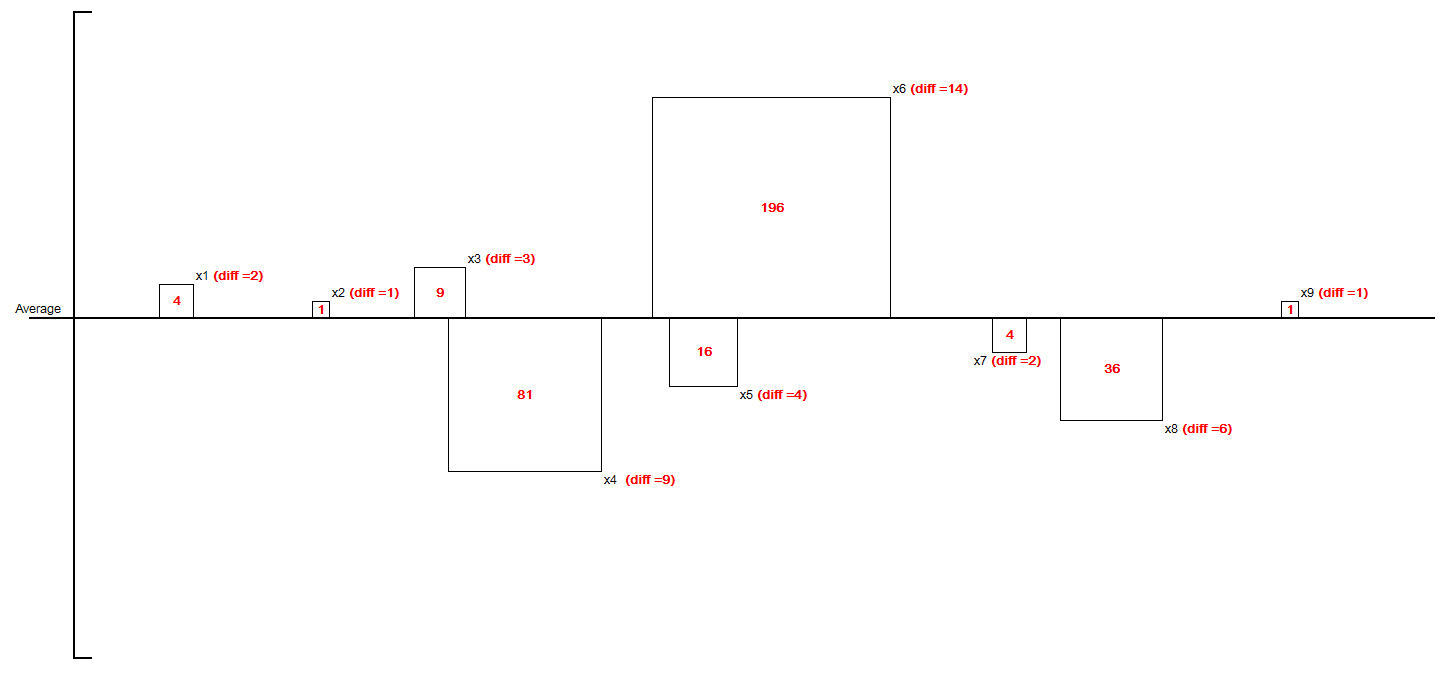
先ほどの、 $ (x_i - \bar{x})^2 $ は図形的に見ると、
「平均からのズレを一片とした正方形の面積を計算している」わけです。
ん?これでは「なぜ二乗せねばいかんのか???」の説明になってない?
そうですね。では、先ほどの標本分散の式、残りの部分を見てみましょう。
\frac{1}{9} \sum_{i = 1}^{9} (i 番目の正方形の面積).
おや?これはどこかで見たような・・・???
と、思った方、そうです。
\bar{x} = \frac{1}{9} \sum_{i = 1}^{9} x_i = \frac{1}{9}(22+21+23+11+16+34+18+14+21) .
ここの真ん中の式ですね!そこに $x_i$ と書いてあったところが、
(i 番目の正方形の面積) と置き換わって書かれているわけです。
さっきまで「くじの番号」だったところが「正方形の面積に置き換わっている」・・・
元の数式は「くじの番号の平均」を求める式だった・・・
つまり????
分散とは正方形の面積の平均サイズを求めていた!
・・・と言うわけです。ここまでご理解いただけましたでしょうか?
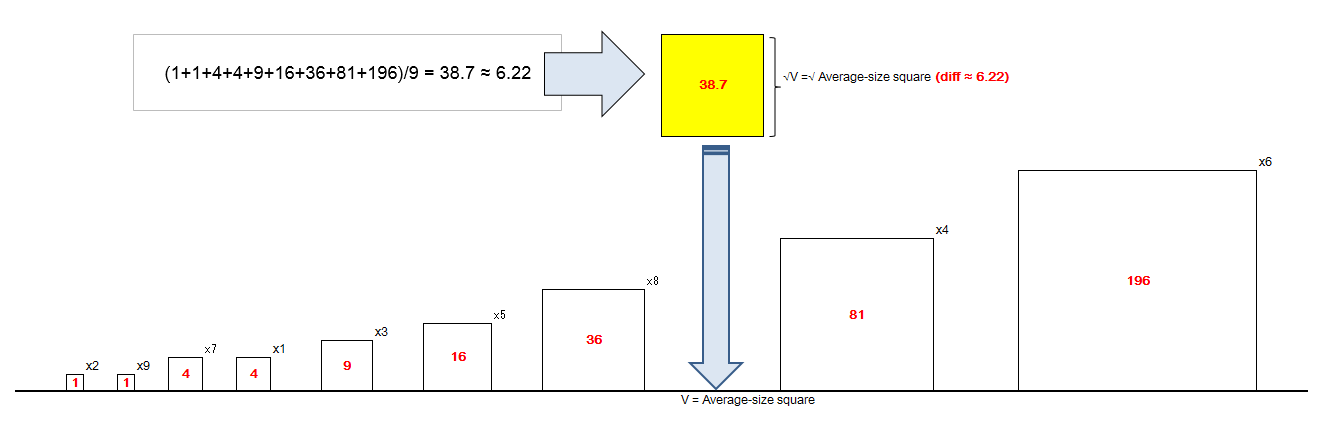
では、わかりやすいように図にしてみましょう。
正方形を小さい方から並べて、平均サイズがどこに入るかを確認すると・・・
この様に、 分散とは「平均値からズレた量を二乗した四角形の平均サイズを求めている」と言うわけです。
ちなみに、標本標準偏差とは、この「平均サイズの正方形の一片」=「平均から平均でどれだけズレているか」を表現しているものになります。
式で表すと・・・正方形の面積から一片の長さを計算するにはルートが使えるので・・・
s = \sqrt{\frac{1}{n} \sum_{I = 1}^{n} (x_i - \bar{x})^2} \\
s = \sqrt{\frac{1}{9} \sum_{I = 1}^{9} (x_i - \bar{x})^2}
ん?まだ「なぜ二乗せねばいかんのか???」の説明になってない?
実はそれを説明するには、標準偏差の話をしなければいけません。
最初私たちは「くじ引きの結果がどれくらいバラついているか」を知りたかったわけです。
それにより、誰が誰の何倍得しているかを知りたいと言う、悪趣味な動機がありました。
この「くじ引きの結果がどれくらいバラついているか」を説明する道具が標本標準偏差になるわけです。
標本標準偏差を計算する事により「誰が誰よりどれだけ得しているか?」がわかるわけです。
で、本当は標本標準偏差が欲しいのに、わざわざ二乗して分散を計算しているのは、
深い理由・・・と言うよりはテクニカルなところがあります。
さて、最初の3人組の話に戻りましょう。
平均から8も少ないAさん、
平均から2少ないBさん、
平均より10多いCさん、
これらの表現を$(x_i - \bar{x})$に準拠した(数学的な)表現に読み替えると。
平均に対して-8のAさん、
平均に対して-2のBさん、
平均に対して+10のCさん、
先ほどまでの図をイメージしながら考えてください。
「くじ引きの結果がどれくらいバラついているか」を誰にでも一言で説明する為には、
この「3人の『平均からの差』の平均は○○だよ」と言えると、
「ああ、個別色々あるけど、全体で大体○○ズレてるのね」と理解ができるわけです。
先ほど、「くじ引きの結果がどれくらいバラついているか」がいわゆる標本標準偏差だと言ったのを思い出してください。
これを、誰にでも一言で説明する為に、平均からの差の平均を説明するのが「わかりやすい」。
この「わかりやすい」が重要で、わかりやすくする為の道具が標本標準偏差と言うわけです。
つまり、「3人の『平均からの差』の平均は○○だよ」の、
「『平均からの差』の平均」が標準偏差と言う概念であり、
○○の部分が標本標準偏差の数値になるわけです。
なので、
全体として平均からのバラつきは標本分散 56の標本標準偏差が(標本分散の平方根なので)だいたい7.5になりますね。
これを基準に「大体7.5のズレは許容範囲」と考えると、
平均に対して-8のAさん、は、平均より損しているし、平均的なズレより更に0.5損している
平均に対して-2のBさん、は、平均より損しているが、平均的なズレの範囲内
平均に対して+10のCさん、は、平均より得していて、平均的なズレより更に2.5得している
と表現でき、
Bさんの飽く無き好奇心は満たされました。
「Aさんの損は8,000円だけど、Cさんの得は10,000円だ。ではCさんの得はAさんに比べてどれくらい違うのかな?」
への答えは、数値化する事で見えてきました。例えば、
「Aさんは平均的なズレ幅より余計に500円損していて、Cさんは平均的なズレ幅より余計に2,500円得しているなぁ」
と言えるわけです。
「余計に500円損しているAさんはに、余計に2,500円得しているCさんは500円のドリンク一杯奢ってもいいんじゃないかな」
・・・とBさんが考えるかは別の話ですが・・・
で、なんでわざわざ二乗を使っているかと言うと「平均からの差の平均」は、
マイナスが入っていると計算ができないんですよね。
だから、わざわざ二乗してマイナスを無くしてから、平方根で元に戻すと言う作業をしています。
絶対値を使えばいいじゃない?
計算してみてください。絶対値を使った場合と二乗を使った場合だと、答えが変わります。
では、どっちがいいのか?
そこについて話すとまた長くなるので、
今のところは「二乗を使った方が便利だからそっちをみんな使うんだよ」、
と言ったところで、お茶を濁しておきます。
さて、前回、
「少し先回りして予告すると、
なぜ、統計の世界では「期待値を平均とも呼ぶのか」について話したいと思います。
これは、会社の同僚に説明した時に割と反応の良かった説明なので、
学生の頃に、平均と期待値は別物として頭に刷り込まれている方、
ちょっと期待していてください。」
と言ったんですが、先に平均-標本分散-標本標準偏差について簡単に説明して、
イメージを作っておいていただいた方がいいと思い、先延ばしにしています。
次回は不偏分散/標準偏差について簡単に説明し、
連続の世界の数式定義まで記載することが目標です。