1章 記述統計の基本と基本的な確率分布 〜1.1 確率関数と記述統計
※この投稿はシリーズものの一部です。
part4 <-[part0](http://qiita.com/yuusei/items/49a63f4402afc66243e6)->part6
注意)このエントリは下記の章立てたシリーズの最初の章のエントリとなります。
これらのエントリは数式を理解する為に絵が多く入っています。
ただし、当然数式も多く入っている為、あまり耐性のない方は無理をせず閉じていただければと思います。
1章 記述統計の基本と基本的な確率分布 (平均/分散/標準偏差/共変動と相関/一様分布/ガウス分布 etc…)
2章 推計統計の基本と対応する確率分布 (検定/推定/t分布/χ二乗分布/F分布 etc…)
3章 様々な確率分布 (二項分布/ポアソン分布/負の二項分布/対数正規分布/指数分布/アーラン分布/ガンマ分布 etc…)
4章 確率過程を理解する為の基礎概念 (確率空間/独立性/ルベーグ積分/大数の弱・強法則/フーリエ変換/中心極限定理 etc…)
5章 確率過程入門 (ウィーナー過程/レヴィ過程/ガウス過程/マルコフ過程/MCMC etc…)
6章 確率的最適化入門 (確率過程の入った待ち行列理論 / 確率的最適制御-動的計画法)
それでは始めます。
1章 記述統計の基本と基本的な確率分布
この章の目標は、平均や分散、標準偏差などを3次元までのレベルで絵を記載して理解できるようにするのが目標です。
著者の好みでわけのわからないこだわりが入る場合がありますが、なるべくわかりやすく書いていきたいと思います。
1.1 確率関数と記述統計
この節では、まず確率関数の定義を示し、続けてその定義を基にして、平均や分散、標準偏差や相関を絵にして
説明していきたいと思います。
1.1.1 確率関数(離散-連続)
前回のエントリを見て下さい
1.1.2 同時確率(離散-連続)
世の中には、二つの事が同時に起きる確率を考えなければいけない時があります。
例えば「雨が降る確率」と「電車が10分遅れる確率」ですね。
ビジネスパーソンなら「商談に遅刻」するリスク、
プライベートなら「恋人とのデートに遅刻」するリスクにつながりますかね。
「雨が降るかどうかが、電車が遅れる確率に影響する」と仮定し(実際降ると遅れる)、
「降る」「降らない」、「遅れる」「遅れない」でマトリックスを書くと
| 電車が遅れない | 電車が遅れる | ||
|---|---|---|---|
| 雨が降らない | 雨が降らないし電車は遅れない確率 | 雨が降らないが電車が遅れる確率 | 雨が降らない確率 |
| 雨が降る | 雨が降るが電車は遅れない確率 | 雨が降って電車も遅れる確率 | 雨が降る確率 |
| 電車が遅れない確率 | 電車が遅れる確率 |
ここで、数学の世界に落とし込むための準備として、
「雨」と「電車遅延」と言う現象をそれぞれ$(雨, 電車遅延) = (x, y)$ とまとめ、
発生する/しない場合を、それぞれ下記のように表現するとします。
x = \begin{cases}
0 & (雨が降らない) \\
1 & (雨が降る)
\end{cases}
y = \begin{cases}
0 & (電車は遅れない) \\
1 & (電車が遅れる)
\end{cases}
また、$x$と$y$が同時に発生する確率を ${\rm P} (x, y)$と表記するとします。
前置きが長くなりましたが、これが「$x$と$y$の同時確率」と言う事になります。
これをさっきのテーブルに当てはめ、適宜確率を割り振ると、
| $y = 0$ | $y = 1$ | ${\rm P} (x)$ | |
|---|---|---|---|
| $x = 0$ | ${\rm P} (0, 0) = 0.5$ | ${\rm P} (0, 1) = 0.2$ | ${\rm P} (x = 0) = 0.7$ |
| $x = 1$ | ${\rm P} (0, 0) = 0.2$ | ${\rm P} (0, 0) = 0.1$ | ${\rm P} (x = 1) = 0.3$ |
| ${\rm P} (y)$ | ${\rm P} (y = 0) = 0.7$ | ${\rm P} (y = 1) = 0.3$ |
となります。さっきのテーブルと比べると、
| 電車が遅れない | 電車が遅れる | ||
|---|---|---|---|
| 雨が降らない | 雨が降らないし電車は遅れない確率 = 50% | 雨が降らないが電車が遅れる確率 = 20% | 雨が降らない確率 = 70% |
| 雨が降る | 雨が降るが電車は遅れない確率 = 20% | 雨が降って電車も遅れる確率 = 10% | 雨が降る確率 = 30% |
| 電車が遅れない確率 = 70% | 電車が遅れる確率 = 30% |
となるわけです。
ここで同時確率を数式で表現しておきます。
離散の世界での同時確率の定義は下記のようになります。
$\forall x, \forall y \in \mathbb {Z}$ なる変数の組$(x, y)$ に対して、
(翻訳:整数の集合$\mathbb {Z} =$ {$\cdots , -2, -1, 0, 1, 2, \cdots $} に含まれるどんな$x$と$y$の組を選んでも)
確率関数 P$(x, y)$を下記で定義します。
\begin{eqnarray}
{\rm P} (x, y) & \geq & 0 & , \\
\sum_{x \in \mathbb{Z}} \sum_{y \in \mathbb{Z}} {\rm P} (x, y) & = & 1 & .
\end{eqnarray}
つまり、全てのP$(x, y)$の組み合わせを合計すると、100%になるわけです(上の表で確認して下さい)。
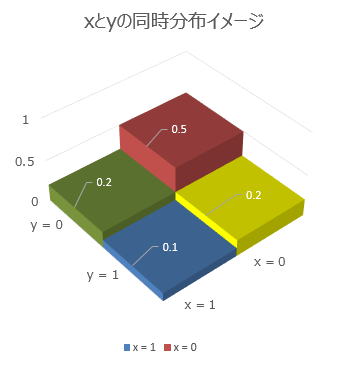
これを絵に描くと
となります。それぞれのブロックを全部積み上げると、高さが1 = 100%になります。
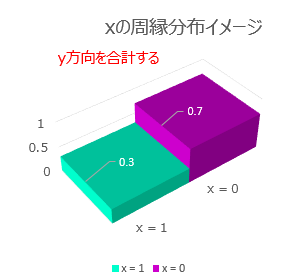
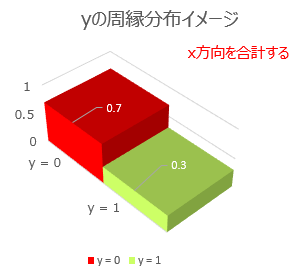
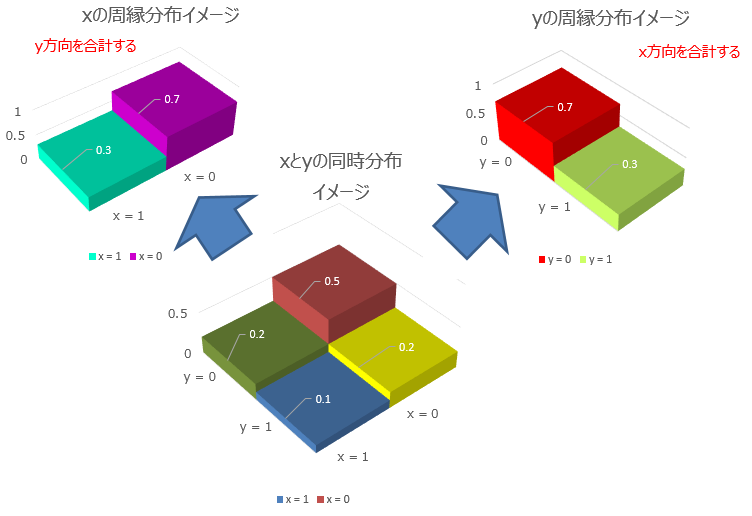
また、それぞれのブロックを2個ずつ(x軸方向とy軸方向)合計すると、
P$(x = 0)$, P$(x = 1)$, P$(y = 0)$, P$(y = 1)$ が計算できます。
つまり、なるべく一目でわかるように書くと、こうなります。
これでなんとなく雰囲気をわかってもらえたでしょうか?
本当は連続バージョンまで定義したかったんですが、時間がなくなったので次回に回します。
連続バージョンはこちら->1.1.3 同時確率(連続)