前回まで母集団を全数調査することを前提に Hadoop について色々と説明をしてきたわけですが、母数の分布について何らかの仮定をした際に適合度の検定が必要になります。
検定によってわかること
検定によってどんなことが判定出来るか考えてみましょう。
- 比率の検定
比率の差の検定 → 2 つの異なる母集団の間で母比率に差があるといえるか。
これは母比率 P がある値 P_0 に等しいと言えるかで判定します。
- 平均値の検定
平均値の差の検定 → 2 つの異なる母集団の間で母平均に差があるといえるか。
これは母集団の平均値 μ がある値 μ_0 に等しいと言えるかで判定します。
- 分散の検定
分散の差の検定 → 2 つの異なる正規母集団の間で分散に差があるといえるか。
これは正規母集団の分散 σ^2 がある値 σ^2_0 に等しいと言えるかで判定します。
- 適合度の検定
観察されたデータが特定の分布に一致していると言えるか。
2 つの母集団の確率分布が異なるものであるかどうか。
ポアソン分布
ポアソン分布については以前に仮説検定と確率分布でも説明した通りです。
確率変数の取りうる値が離散かつ無限の場合、単位時間あたり平均で λ 回発生する事象が単位時間に X 回発生する確率です。
{P(X = k) = \frac {{\lambda}^xe^{-\lambda}} {k!} \\
ただし \\
\lambda \gt 0
}
分布の適合度の検定
ある位置情報における端末固有情報の観測回数を考えます。端末固有情報がそれぞれ特定の地域で観測されるか 100 台について調査したとして、端末固有情報毎に以下の表に従ったとします。
| 観測回数 | 端末台数 |
|---|---|
| 0 | 43 |
| 1 | 31 |
| 2 | 14 |
| 3 | 8 |
| 4 | 3 |
| 5 | 1 |
この観測回数はポアソン分布に従っていると言えるか有意水準 (= P 値) 5% で検定します。
λ = 未知母数 (データから推定する)
X = クラス k
したがって標本平均をポアソン分布の未知母数 λ の推定値とし
\hat{\lambda} = \frac 1 {100} (0 x 43 + 1 x 31 + 2 x 14 + ... ) = 1
したがって期待度数は
| クラス k | 観測度数 | 期待度数 |
|---|---|---|
| 0 | 43 | 36.8 |
| 1 | 31 | 36.8 |
| 2 | 14 | 18.4 |
| 3 | 8 | 6.13 |
| 4 | 3 | 1.53 |
| 5 | 1 | 0.307 |
| 6 | 0 | 0.0330 |
\chi^2 = \frac {(43-36.8)^2} {36.8} + \frac {(31-36.8)^2} {36.8} + ... = 5.011
こうして求められた値をカイ二乗分布の表と付きあわせます。
自由度はクラスの個数 -1 から未知母数の個数を引くので 7 - 1 - 1 = 5 、仮に k=3 以上をひとまとめにしてクラス数を 4 とした場合は 4 - 1 - 1 = 2 となります。 P 値 0.05 で自由度 2 の欄を見ますと 5.99146 とありますからこの値に収まっており帰無仮説は棄却されません。つまり ポアソン分布に従っていないとは言えない ことがわかりました。
ポアソン分布と極限定理
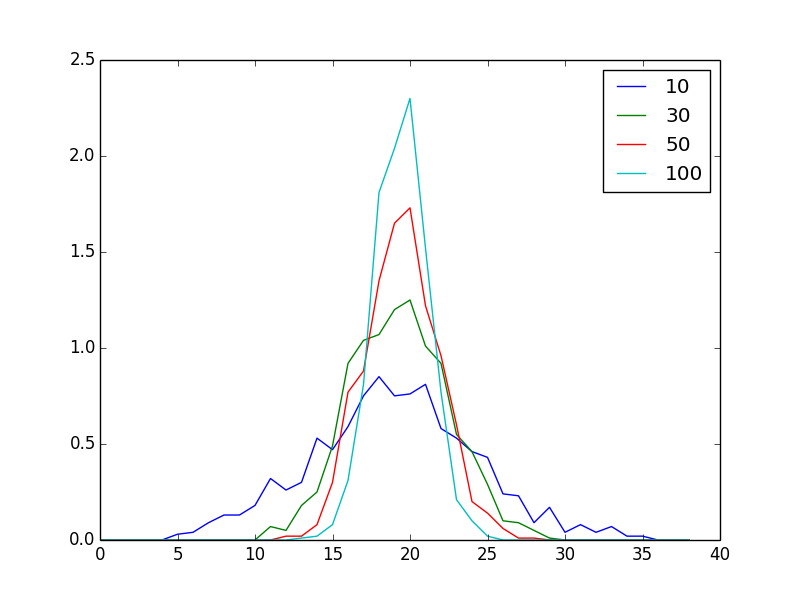
せっかくなのでパラメータが n と p=λ/n な正規分布の λ を一定に保ったまま n を無限大に近づけるとポアソン分布に近似することをシミュレーションしてみましょう。
以前にも中心極限定理のシミュレーションは強引な方法でやりましたが、より簡単におこなうことができます。
import numpy as np
import matplotlib.pyplot as plt
fig = plt.figure()
ax = fig.add_subplot(1,1,1)
M = 1000
for N in [10,30,50,100]:
data = [np.average(np.random.poisson(3, N)) for i in range(M)]
hist, key = np.histogram(data, bins=np.arange(1,5,0.1), density=True)
ax.plot(hist, label=str(N))
plt.legend(loc='best')
plt.show()
plt.savefig("image.png")
N = 100 のとき、ほぼ正規分布に近似していることが観測されます。