昨日は大きなサイズのデータを扱う際に重要な確率の定理である「大数の定理」と「中心極限定理」について説明しました。
今日は実際に計算機を使って多数の確率試行がどのような分布になるかシミュレーションをしてみましょう。
疑似乱数生成
計算機で本物の乱数を作ることはできません。そこで擬似乱数を利用します。 (なお、擬似乱数は正式には手偏の無い「疑似」が正式だそうです。) 乱数は非常に奥が深く、追求するとキリがありません。
ここでは NumPy にそなわっている numpy.random.randint を利用します。これは一様に離散する分布から整数を返します。
40,000 回のコイントスの結果を散布図にする
中心極限定理を応用すると 40,000 回のコイントスで 20,400 回も表が出ることはないと昨日説明しました。定理上は証明されましたが、やはりエンジニアたるもの実際に計算機上で動かしてみないとにわかに納得し難いということもあるでしょう。
そこで以下のコードを使ってシミュレーションします。
def coin_toss(lim):
""" コイントスをシミュレーションする """
# 表が出れば 1 を、裏が出れば 0 を格納
_randomized = np.random.randint(2, size=lim)
# 表が出た回数の総合計を集計する
_succeed = [i for i in _randomized if i == 1]
# 集計結果を返す
return len(_succeed)
X = []
Y = []
lim = 10000
# 40,000 回のコイントスを 10,000 回おこなう
for i in range(lim):
X.append(i)
Y.append(coin_toss(lim = 40000))
print (X)
print (Y)
_over_lim = [i for i in Y if i >= 20400]
# 20,400 以上が出た回数
print( len(_over_lim) )
_under_lim = [i for i in Y if i <= 19600]
# 19,600 以下が出た回数
print( len(_under_lim) )
これで 1 回の実験で 4 億回のコイントスをすることになります。
1 回目の実験結果
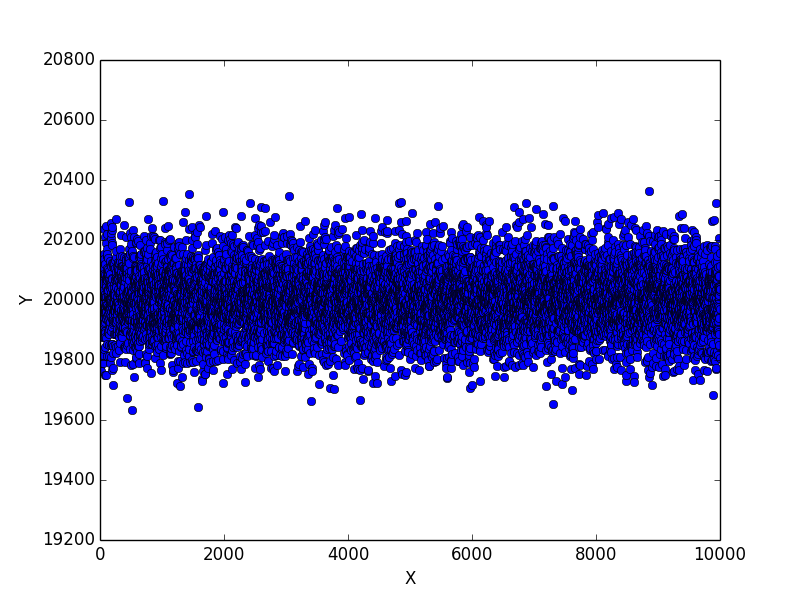
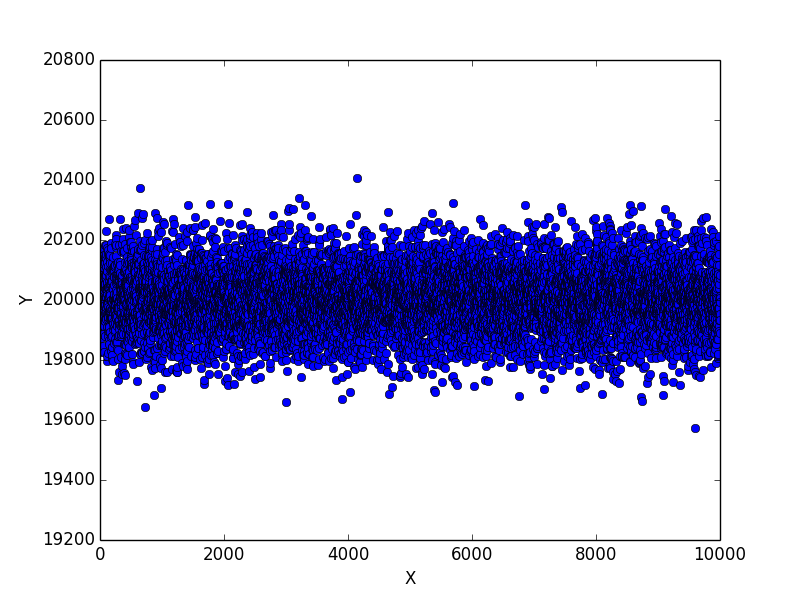
まずは 1 回目の実験結果です。
40,000 回のコイントスで素直に考えれば 20,000 回表が出るはずですが、これを 10,000 回繰り返したグラフがこれです。
ほぼ中心に集まっていますね。今回は表が出た回数が 20,400 回以上にも 19,600 回以下にもなりませんでした。
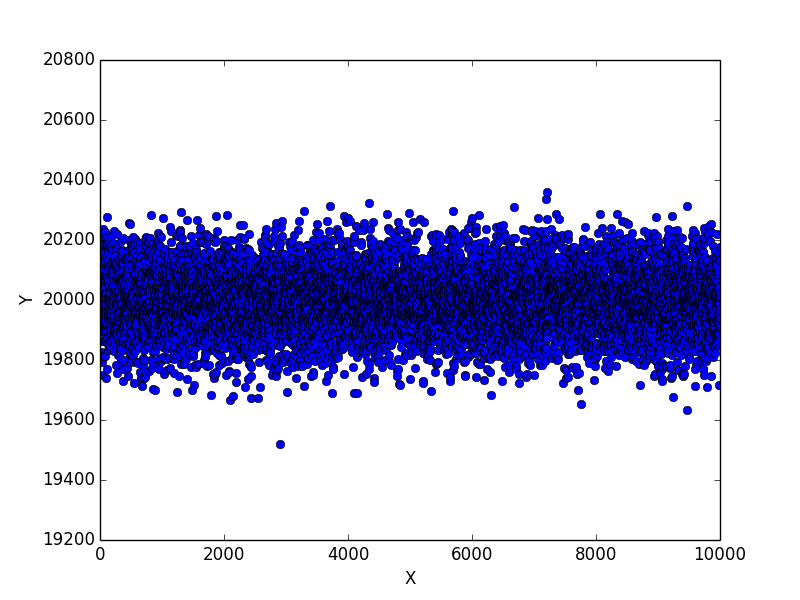
2 回目の実験結果
もう一度実験してみると表が出る回数が 19,600 回以下のケースが 10,000 回中 1 回だけ発生しました。
グラフからなんとか読み取れるかと思います。
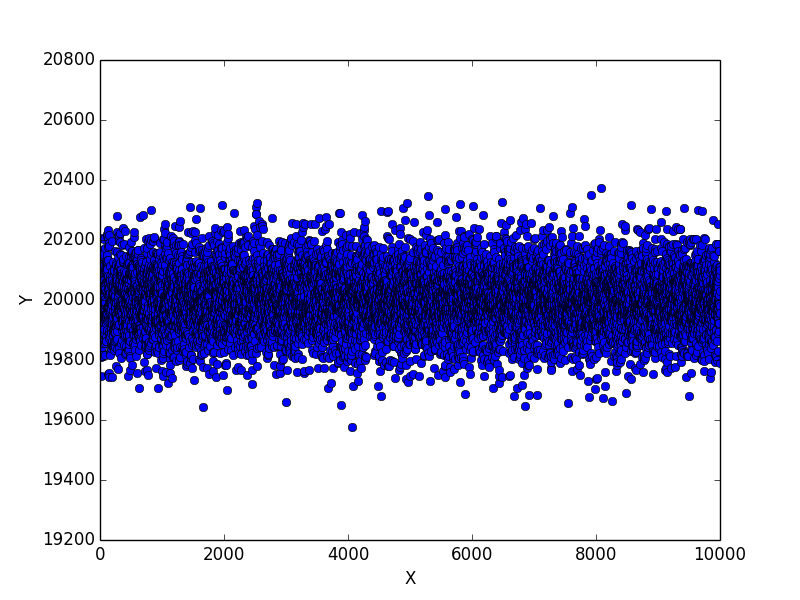
3 回目の実験結果
3 回目の実験結果です。
かろうじて表が出た回数が 20,400 回を超えなかったケースが 1 件だけありました。また 19,600 回を下回るケースが 1 件だけありました。
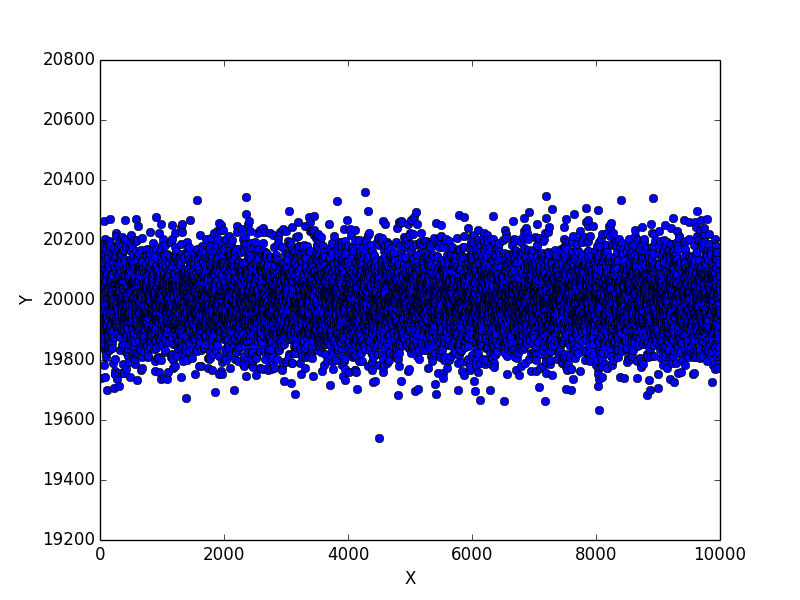
4 回目の実験結果
4 回目の実験結果です。
やはり 20,400 回は超えませんでした。
5 回目の実験結果
追試として、日を改めてもう一度同じ実験をしてみました。
20,400 回以上表が出たケースが 1 件と、 19,600 回以下しか表が出なかったケースが 1 件ずつありました。
仮説検定
さて、それではここで 40,000 回のコイントスで 20,400 回の表が出るという仮説が正しいと言って良いか統計学的に調べてみましょう。
仮説のたて方としては次のようになります。
| 仮説 | 説明 |
|---|---|
| 帰無仮説 | 40,000 回のコイントスで 20,400 回の表が出る |
| 対立仮説 | 40,000 回のコイントスで 20,400 回の表が出ない (20,000 回表が出る) |
カイ二乗検定
ピアソンのカイ二乗検定 (Pearson's chi-square test) は、カイ二乗検定のうち最も基本的かつ広く用いられる方法です。式は次のようになります。
X^2 = \sum\frac {(O-E)^2} {E}
カイ二乗検定の実装
SciPy を利用するとカイ二乗検定は容易に実装できます。
まずは手始めに 400 回のコイントスで 204 回表が出るかどうかを調べてみましょう。調べ方としては表 204 回、裏 196 回出た結果が 400 回のコイントスから出たものであるという仮説が有意であるかどうかを調べます。
# -*- coding:utf-8 -*-
import numpy as np
import scipy.stats
s = 204 # 表が出る回数
f = 196 # 裏が出る回数
e = 200 # 期待される回数
# 帰無仮説 (204:196)
observed = np.array([s,f])
# 対立仮説 (200:200)
expected = np.array([e,e])
# カイ二乗検定をおこなう
x2, p = scipy.stats.chisquare(observed, expected)
print("カイ二乗値は %(x2)s" %locals() )
print("確率は %(p)s" %locals() )
# 統計学的有意水準 0.05 より高いかどうか調べる
if p > 0.05:
print("有意です")
else:
print("有意ではありません")
結果はこうなります。 0.68 は 0.05 よりも高いですから有意ですね。十分起こりえると言えます。
カイ二乗値は 0.16
確率は 0.689156516779
有意です
ではこれを表 2,040 回、裏 1,960 回としてみるとどうでしょう。
カイ二乗値は 1.6
確率は 0.205903210732
有意です
まだ有意のようですね。十分起こりえます。
では次に表 20,400 回、裏 19,600 回ではどうでしょう。
カイ二乗値は 16.0
確率は 6.33424836662e-05
有意ではありません
きわめて低い値 (浮動小数点数に注意) にしかなりませんでした。これはまず起こりえないと言えます。
試しに 40,000 回のコイントスで 20,100 回表が出るかどうか試すとどうなるでしょうか。
カイ二乗値は 1.0
確率は 0.317310507863
有意です
有意ですね。 20,100 回程度であれば表が出ることが十分起こりえるとわかりました。
考察
計算機を利用すると大量の計算をおこないシミュレーションし、その結果を可視化することができます。
また、仮説検定により観察された事象の相対的頻度がある頻度分布に従うかどうか検定することができることがわかりました。