はじめに
前回は、行列を使わずに、三角形の相似比だけを使って、Z座標の値でX座標とY座標を割るだけで、3Dの透視変換が行えることを説明しました。
今回は、シェーダが使っている座標系である同次座標という特徴を活かして、より簡単に3Dの透視変換が実現できることを見てみましょう。
1. 頂点座標データの変更
まず、前回の最後に書いたコードから、頂点データを次のように変更します。
Game::Game()
{
...
std::vector<VertexData> data;
data.push_back({ { -1.0f, 0.0f, 1.0f }, { 1.0f, 0.4f, 0.7f, 1.0f } });
data.push_back({ { 0.2f, -1.0f, 1.0f }, { 1.0f, 0.4f, 0.7f, 1.0f } });
data.push_back({ { 0.2f, 1.0f, 1.0f }, { 1.0f, 0.4f, 0.7f, 1.0f } });
data.push_back({ { -0.2f, 0.0f, 2.0f }, { 0.0f, 0.75f, 1.0f, 1.0f } });
data.push_back({ { 1.0f, -1.0f, 2.0f }, { 0.0f, 0.75f, 1.0f, 1.0f } });
data.push_back({ { 1.0f, 1.0f, 2.0f }, { 0.0f, 0.75f, 1.0f, 1.0f } });
std::vector<GLushort> indices;
indices.push_back(0);
indices.push_back(1);
indices.push_back(2);
indices.push_back(3);
indices.push_back(4);
indices.push_back(5);
...
glClearColor(0.0f, 0.0f, 0.0f, 1.0f);
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
}
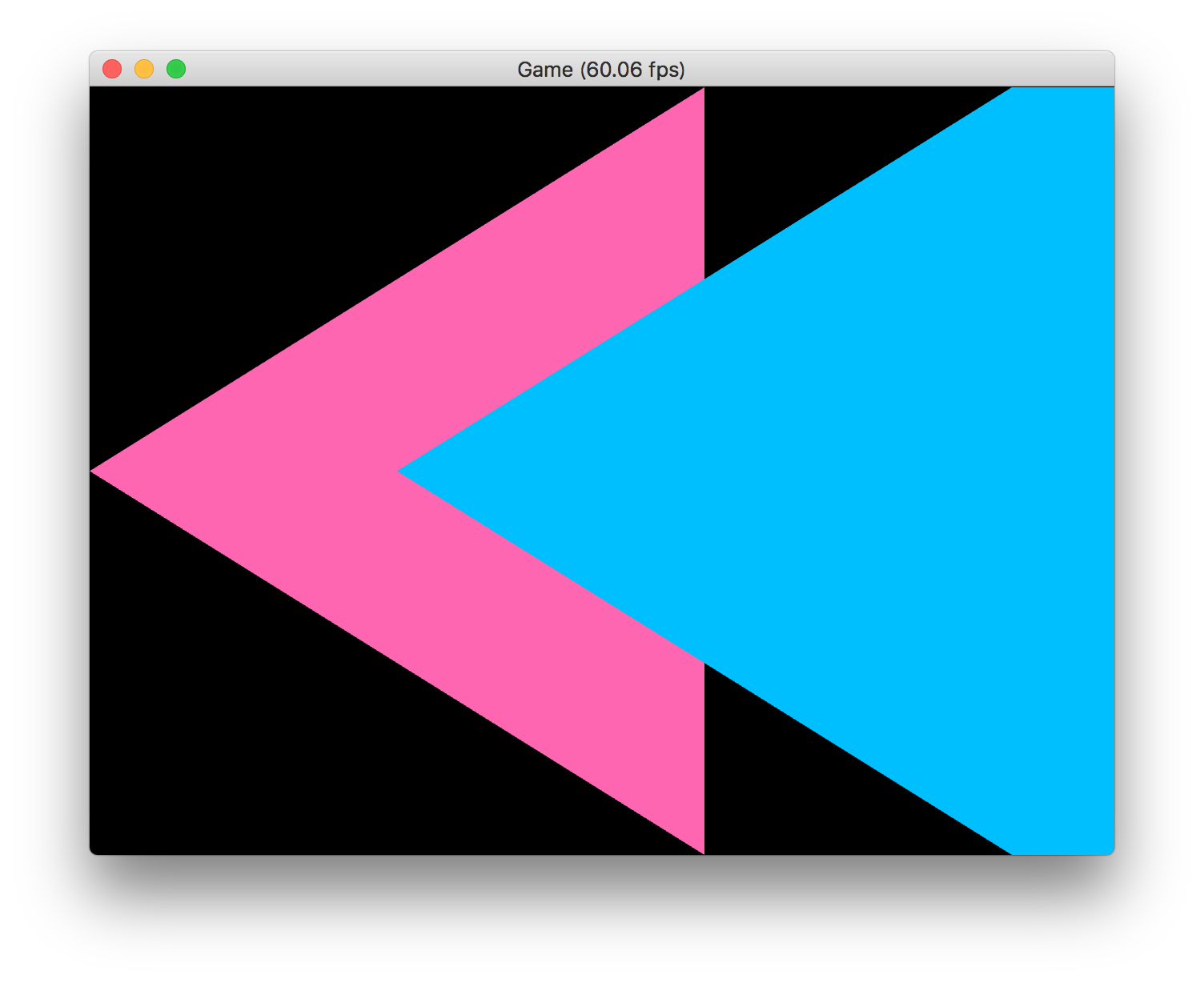
ピンクの三角形がz=1.0のZ平面上に、同じ大きさの水色の三角形がz=2.0のZ平面上に配置されています。
2. 同次座標を使って割り算する
次にこのデータをレンダリングするための頂点シェーダの実装を、次のように変更します。
# version 410
layout (location=0) in vec3 vertex_pos;
layout (location=1) in vec4 vertex_color;
uniform mat4 proj_mat;
out vec4 color;
void main()
{
gl_Position = vec4(vertex_pos.x,
vertex_pos.y,
vertex_pos.z - 0.01,
vertex_pos.z);
color = vertex_color;
}
前回の頂点シェーダの実装よりもだいぶ短くなりました。Z座標の遠さから計算した相似比を使ってX座標やY座標を変換するのが透視変換だと説明したばかりなのに、割り算がどこにも見当たりません。これで本当に大丈夫でしょうか?
実行してみましょう。これだけで、前回と変わらない結果が出力されます。
ここまでのプロジェクト:MyGLGame_step3-2.zip
Z座標の計算に問題がないことを確認するために、頂点データを次のように書き換えて、水色の三角形をz=0.5のZ平面上に移動してみましょう。
std::vector<VertexData> data;
data.push_back({ { -1.0f, 0.0f, 1.0f }, { 1.0f, 0.4f, 0.7f, 1.0f } });
data.push_back({ { 0.2f, -1.0f, 1.0f }, { 1.0f, 0.4f, 0.7f, 1.0f } });
data.push_back({ { 0.2f, 1.0f, 1.0f }, { 1.0f, 0.4f, 0.7f, 1.0f } });
data.push_back({ { -0.2f, 0.0f, 0.5f }, { 0.0f, 0.75f, 1.0f, 1.0f } });
data.push_back({ { 1.0f, -1.0f, 0.5f }, { 0.0f, 0.75f, 1.0f, 1.0f } });
data.push_back({ { 1.0f, 1.0f, 0.5f }, { 0.0f, 0.75f, 1.0f, 1.0f } });
実行結果は次のようになります。
見事に水色の三角形がピンクの三角形よりも手前に表示されて、正確にZ座標の計算ができていることが分かりますね!
3. 同次座標の計算について
頂点シェーダの実装をもう一度見てみましょう。gl_Position変数に頂点座標を代入しているのは次のコードです。割り算の記号「/」も掛け算の記号「*」も書かれていないのに、なぜ相似比に基づいた割り算が実現できているのでしょうか?
gl_Position = vec4(vertex_pos.x,
vertex_pos.y,
vertex_pos.z - 0.01,
vertex_pos.z);
その答えは、**シェーダが使用している特別な座標系(同次座標)**にあります。ポイントは第3引き数のZ座標から0.01という小さな値を引いていることと、これまで1.0を渡していた第4引数にZ座標を渡していることです。
シェーダが使用している座標系は、ただの3次元空間ではありません。これまで何気なく**gl_Position変数に頂点データを代入するコード**を書いてきたと思いますが、その右辺値は3次元ベクトルではなく、常に4次元ベクトルでした。このことを不思議に思っていた方もいるのではないでしょうか?
シェーダが使用している座標系では、頂点座標は同次座標と呼ばれる4次元ベクトルとして、X座標, Y座標, Z座標の3つの値にプラスして、第4の値wを伴って表されます。そして、X座標、Y座標、Z座標の最終的な値は、第4の値wによって割られた値が使われるのです。
すなわち、次のような頂点データがgl_Position変数に代入されたとすると、
v =
\left(
\begin{matrix}
x & y & z & w
\end{matrix}
\right)
その最終的な値は次のように計算され、この値が実際のレンダリング時に使用されます。
v' =
\left(
\begin{matrix}
\frac{x}{w} & \frac{y}{w} & \frac{z}{w}
\end{matrix}
\right)
これまでのコードにおいては、wに常に1.0を指定してきたので、X座標、Y座標、Z座標に指定した値が、そのまま使われてきたのです(1で何を割っても元の値のままですね)。
ちなみに
wに0.0を指定すると、0で何を割っても無限大となるので、実用的な値が定まりません。そのため、wに0.0を指定した時には何も描画されなくなってしまいます。変換前のwの値には常に1.0を指定するのだということを覚えておきましょう。
では、今回の頂点シェーダにおける値はどのようになるでしょうか? gl_Position変数には、次のような値が渡されています。
v =
\left(
\begin{matrix}
x & y & z-0.01 & z
\end{matrix}
\right)
奇妙に思われるかもしれませんが、Z座標にもW座標にも、zの値を入れているのです。これがミソです。先程の要領で、同次座標において最終的に計算される値を出してみましょう。X座標, Y座標, Z座標を、すべてW座標の値で割ります。するとこうなります。
v' =
\left(
\begin{matrix}
\frac{x}{z} & \frac{y}{z} & \frac{z-0.01}{z}
\end{matrix}
\right)
X座標もY座標もZ座標の値で割られるので、Z座標が大きくなればなるほど、すなわち頂点がカメラから離れるほど、値が小さくなっていくことが分かります。そう、これだけでちゃんと透視変換が行えているのです。
なお、Z座標から0.01の値を引いているのが意味のないように見えるかもしれませんが、0.01を引いておかないと、Z座標を同じZ座標で割り算することになり、Z座標の値が常に1.0になってしまいます。そのため、元のZ座標の値が1.0でも2.0でも、同じZ座標で描画されていることになってしまい、デプステストが正常に機能しなくなります。
そこで、Z座標の値はW座標の値で割る前に小さな値を引いておく、という前処理を入れることによって、Z機能の値の大小が保存されるようになります。たとえばz=1.0のときは、(z-0.01)/z = 0.99/1.0 = 0.99となります。また、z=2.0のときは、(z-0.01)/z = 1.99/2.0 = 0.995となります。1.0 < 2.0の関係と、0.99 < 0.995の大小関係は変わらないので、小さな値を引くだけで正常にZ座標の大小が扱えるようになることが分かります。
Z座標から引く小さな値は、今回は0.01としていますが、Z座標に0.01よりも小さな値を指定する場合には、さらに小さな値(たとえば0.00001など)を指定します。
4. まとめ
今回は、シェーダが採用している同次座標の性質を活用して、3Dの透視変換が行えることを説明しました。
- 同次座標の
wの値にZ座標の値を入れる。 - Z座標の値から少し小さな値を引いておく。
という2点の事柄を守るだけで、複雑な計算をせずに3Dの透視変換が行えるのです。もちろんこれは偶然のことではなく、そういった利点が最大限に得られるように、シェーダの座標系を同次座標として扱うようにOpenGLのプログラミング環境が設計されているわけです。
次回は、今回やった同次座標を活用した透視変換をさらに応用できるように、行列を使った計算を導入してみましょう。