はじめに
前回の記事で、頂点データをGLKitフレームワークのベクトル構造体を使って扱いやすくしましたので、今回からは3次元的な表示ができるように、少しずつ数学的な計算を入れていきましょう。
3次元的な表現をするときには、通常は行列を使って座標変換をしていくのですが、GLSLでの座標変換の特性が分かりやすいように、今回は行列を使わずに座標変換するテストをしてみたいと思います。こうすることで、行列がどのような働きをしているのかも理解しやすくなると思うのです。
OpenGLの描画を試していると、初心者的に「なんで?」と思うポイントがいくつもあります。この記事では、それを1つずつ説明して、初心者がつまづくことなく透視変換や3Dデータの描画を理解できるようにしたいと思います。
1. データにZ方向の奥行きを付けてみる
これまで図形を描画する時には、Z座標の値を0.0に固定してきましたが、今回は奥行きを変えた2つの三角形を書いてみましょう。
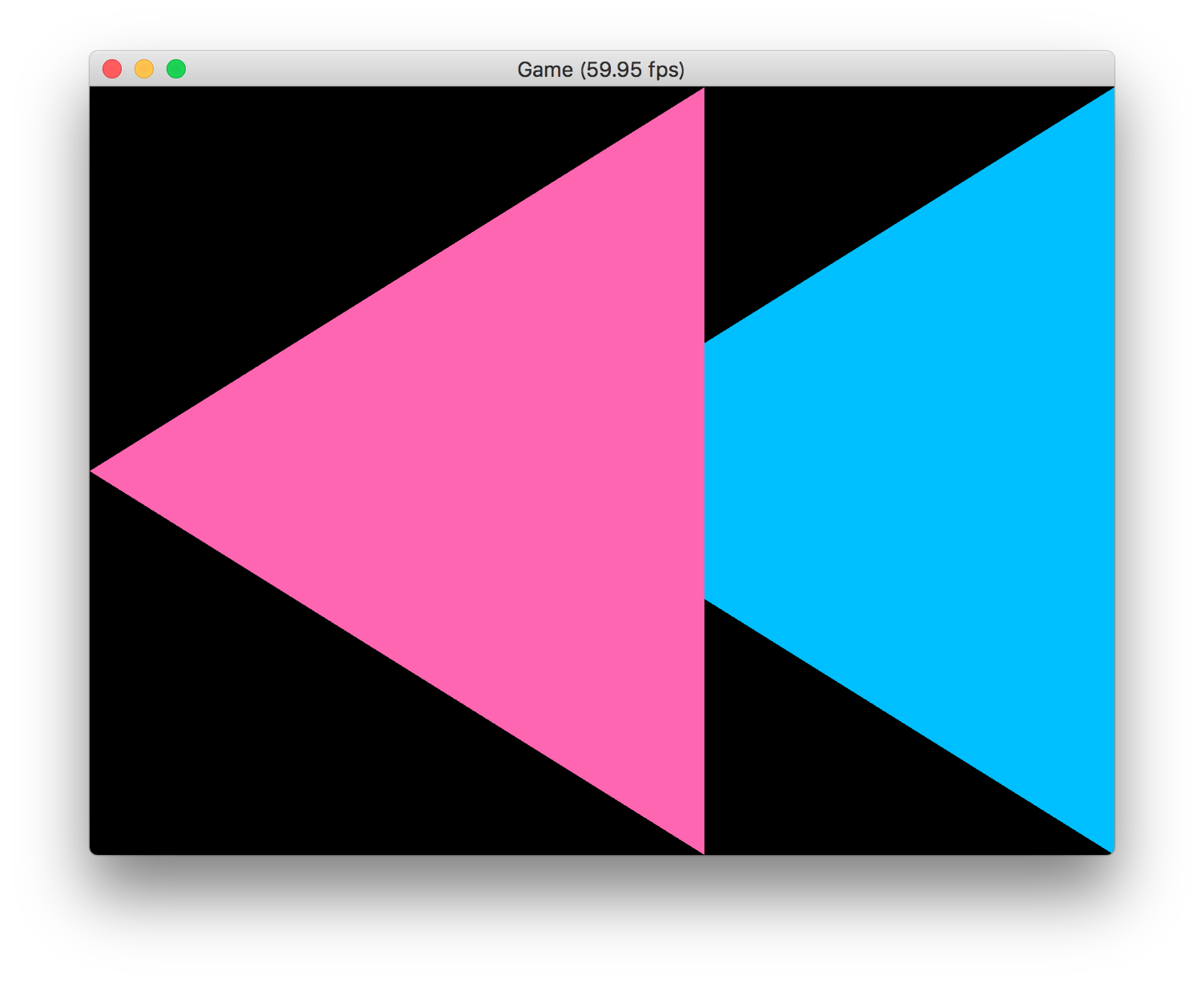
まずは頂点データを次のように用意してみます。1つ目の三角形はZ座標が1.0で、2つ目の三角形はZ座標が2.0です。1つ目の三角形の色はピンク色に、2つ目の三角形の色は水色にしています。今回は色の違いが分かりやすいように、UV座標は省いて、テクスチャ表示はオフにしています。
struct VertexData
{
GLKVector3 pos;
GLKVector4 color;
};
Game::Game()
{
...
std::vector<VertexData> data;
data.push_back({ { -1.0f, 0.0f, 1.0f }, { 1.0f, 0.4f, 0.7f, 1.0f } });
data.push_back({ { 0.2f, -1.0f, 1.0f }, { 1.0f, 0.4f, 0.7f, 1.0f } });
data.push_back({ { 0.2f, 1.0f, 1.0f }, { 1.0f, 0.4f, 0.7f, 1.0f } });
data.push_back({ { -0.2f, 0.0f, 2.0f }, { 0.0f, 0.75f, 1.0f, 1.0f } });
data.push_back({ { 1.0f, -1.0f, 2.0f }, { 0.0f, 0.75f, 1.0f, 1.0f } });
data.push_back({ { 1.0f, 1.0f, 2.0f }, { 0.0f, 0.75f, 1.0f, 1.0f } });
std::vector<GLushort> indices;
indices.push_back(0);
indices.push_back(1);
indices.push_back(2);
indices.push_back(3);
indices.push_back(4);
indices.push_back(5);
...
}
void Game::Render()
{
...
glDrawElements(GL_TRIANGLES, 6, GL_UNSIGNED_SHORT, (void *)0);
}
この他、テクスチャ関係の変数宣言を削除し、UV座標を転送するためのコードも削除します。詳しくは、下部にある「ここまでのプロジェクト」のコード実装を参照してください。
シェーダ(頂点シェーダおよびフラグメント・シェーダ)のコードをテクスチャ描画を伴わない「2-3. 頂点のインデックス・リストを使って描画する」の時点のものに戻します。頂点シェーダは次の通りです。
# version 410
layout (location=0) in vec3 vertex_pos;
layout (location=1) in vec4 vertex_color;
out vec4 color;
void main()
{
gl_Position = vec4(vertex_pos, 1.0);
color = vertex_color;
}
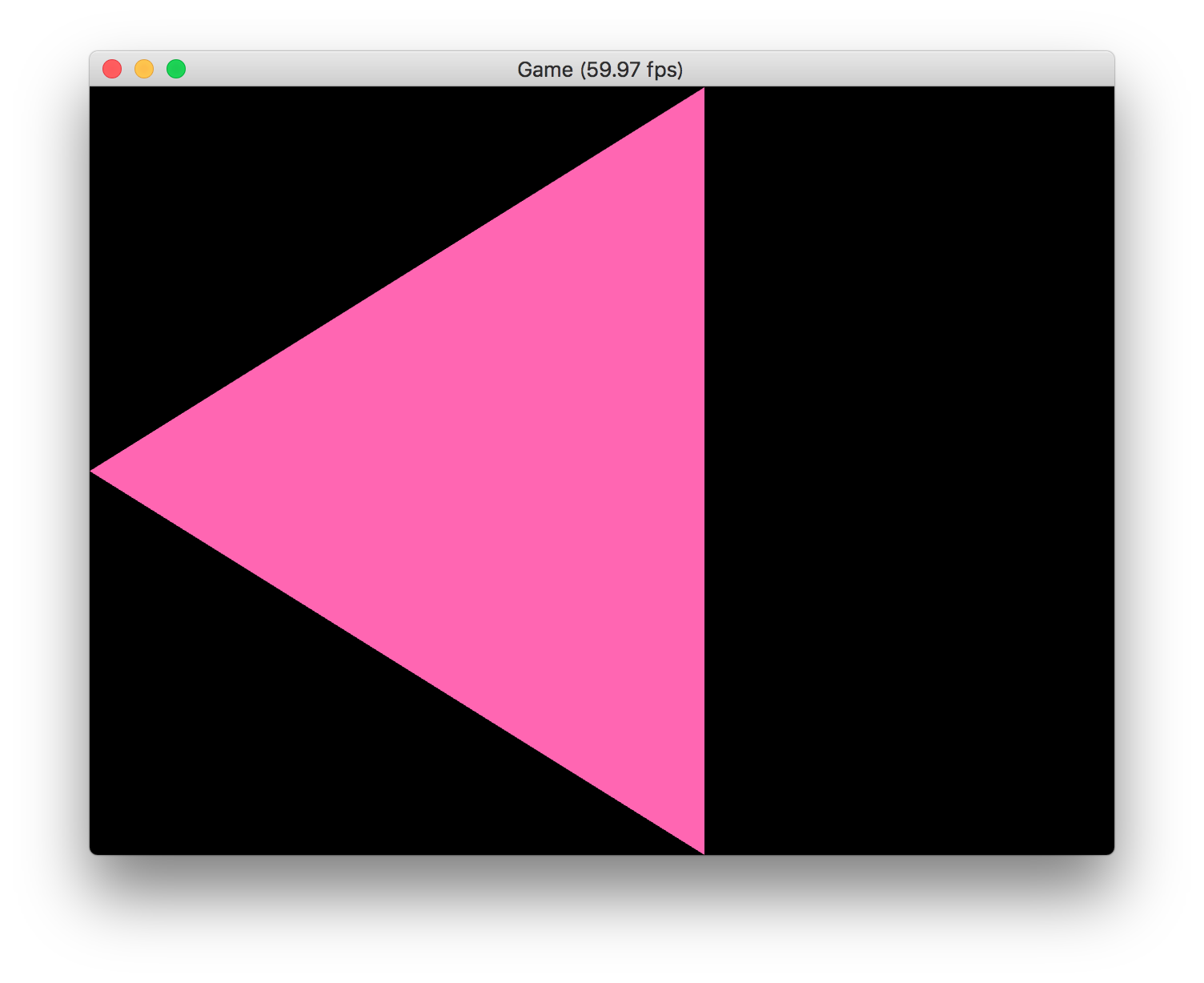
これを実行してみると、実行結果は次のようになります。
ここまでのプロジェクト:MyGLGame_step3-1a.zip
あれ? 三角形を2つ描画しているはずなのに、1つしか表示されていませんね。これはなぜでしょう?
2. 三角形が表示されない? クリッピング領域とは
三角形がなぜ1つしか描画されていないのかというと、GLSLで描画するデータは、Z座標が-1.0〜1.0の範囲に収まっている必要があるからです(これをクリッピング領域と言います)。2つめの三角形のZ座標を2.0にしていたので、この領域を越えてしまったために描画されなくなっているのですね。
そこで、次のように頂点シェーダのコードを書き換えてみましょう。
# version 410
layout (location=0) in vec3 vertex_pos;
layout (location=1) in vec4 vertex_color;
out vec4 color;
void main()
{
gl_Position = vec4(vertex_pos.x,
vertex_pos.y,
vertex_pos.z / 10.0,
1.0);
color = vertex_color;
}
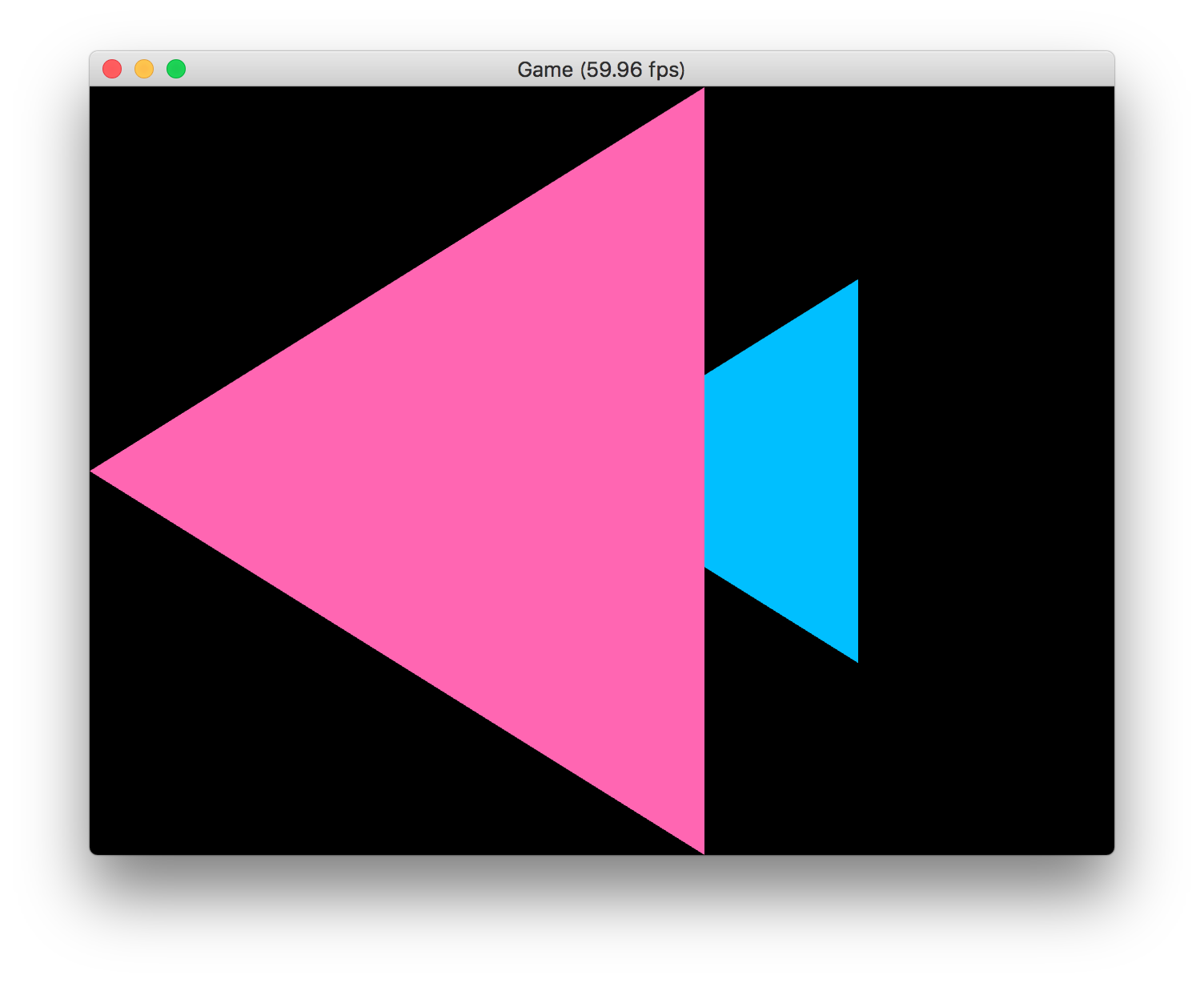
Z座標の値をそのまま使うのではなく、1/10にした値を使うように変更しました。これで実行してみましょう。
ここまでのプロジェクト:MyGLGame_step3-1b.zip
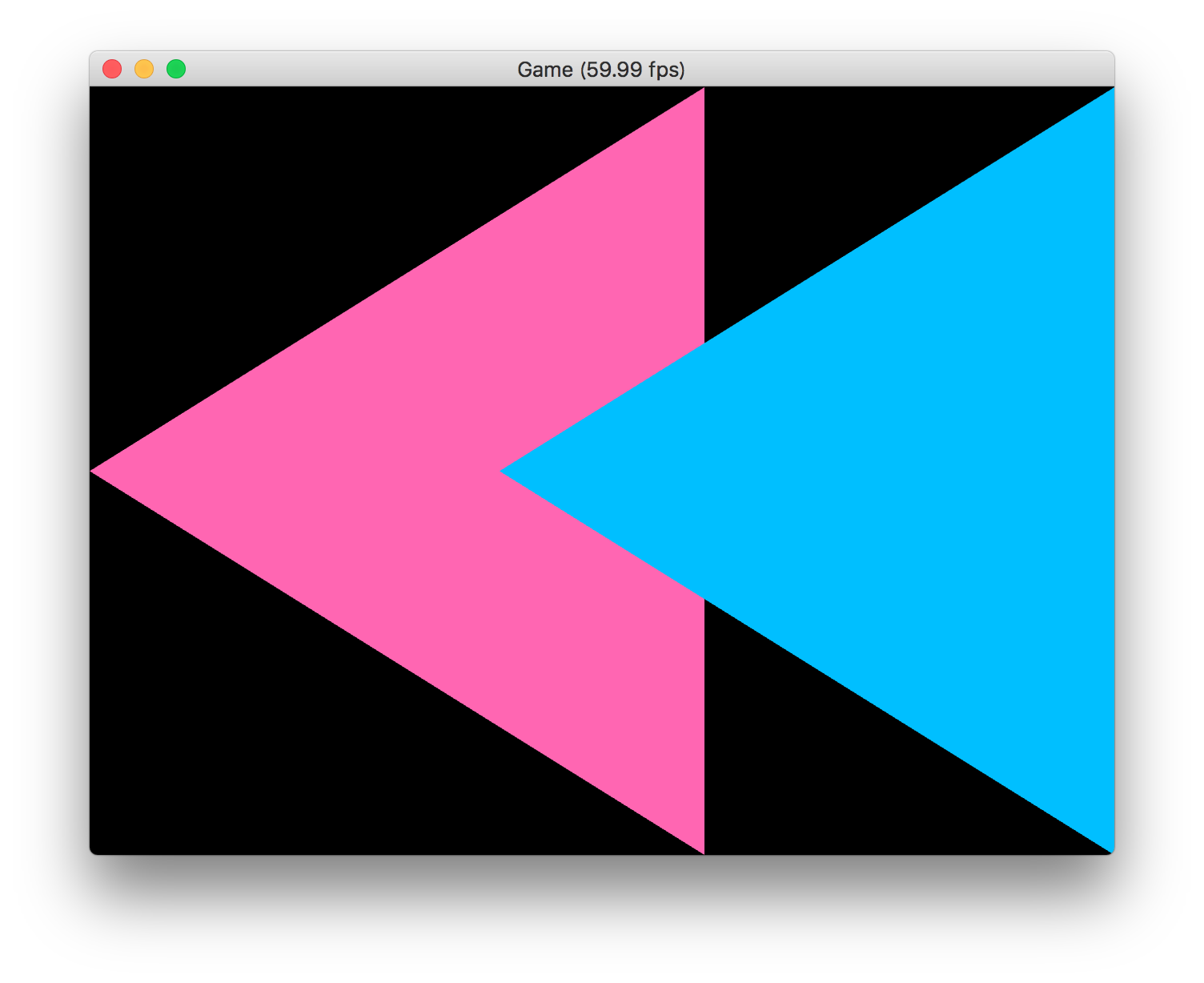
Z値がクリッピング領域の範囲内に収まるようになったので、三角形が2つ表示されるようになりました。
3. 三角形の正しい順番は? デプステストの有効化
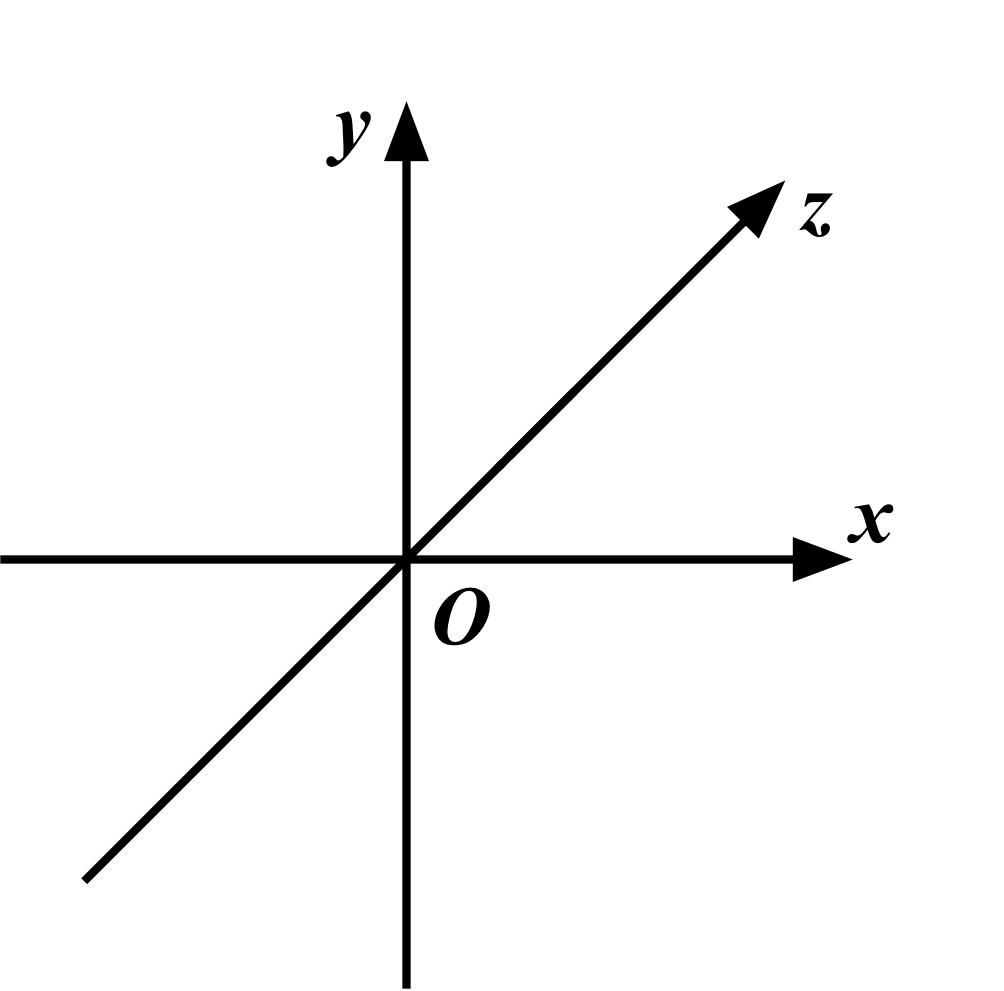
三角形が2つとも表示されるようになりましたが、水色の三角形がピンク色の三角形の上に表示されていますね。ここで、GLSLで図形がレンダリングされる空間の座標系について確認しましょう。
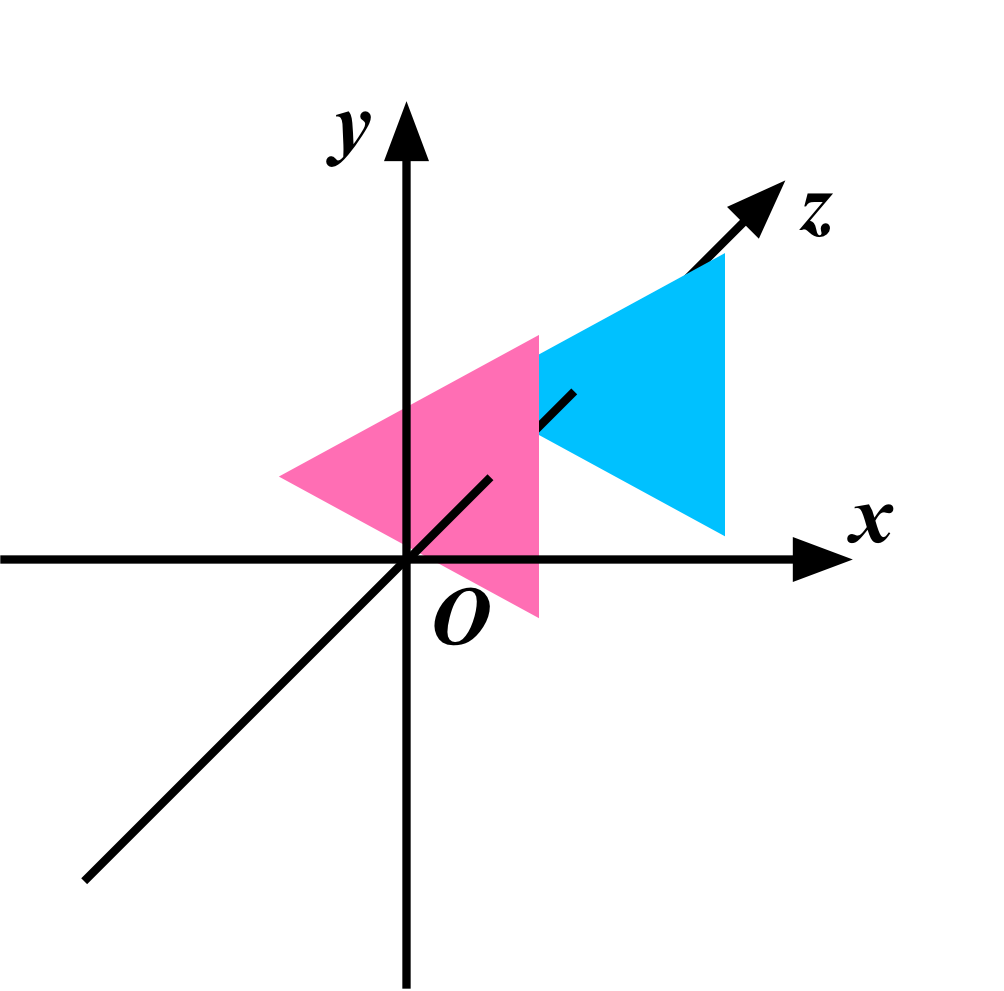
この座標系の上に、先程定義した頂点データをプロットしてみると、次のようになります。
この前後関係を見ると、本来はピンク色の三角形の方が上に来るはずなのですが、実行画面を見てみると、水色の方が上に来ています。これはなぜでしょうか?
答えは、現在はデプステストが行われていないので、描画された順に上書きされていっているためです。インデックス・リストの順番に沿って描画される時には水色の方が後で描画されるので、こちらが手前に表示されているのですね。デプステストが有効になっていない場合、Z座標は使われず、前後関係は描画の順番だけで決まるのです。
それでは、デプステストを有効にしてみましょう。Gameクラスのコンストラクタに、デプステストを有効にするためのglEnable()関数呼び出しのコードを追加します。また、glClear()関数で画面をクリアするところも、色情報に加えて深度情報もクリアするように、GL_DEPTH_BUFFER_BIT定数を加えます。
Game::Game()
{
glEnable(GL_DEPTH_TEST);
...
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
}
void Game::Render()
{
...
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
...
}
デプステストを有効にすると同時に、NSOpenGLViewクラスのインスタンスを作成するときに指定する
NSOpenGLPixelFormatAttribute型の定数を使ってNSOpenGLPFADepthSizeのキーに対応した値として、16ビット, 24ビット, 32ビットのいずれかの値を指定しなければいけません。この設定は、第1回でプロジェクトを作成した時点で行っていて、32ビットの値を指定済みです。
すると実行結果は次のようになります。各フラグメントにおけるZ座標の大小が比べられるようになり、Z座標の値が小さいピンク色の三角形の方が手前に描画されるようになりました。三次元空間の三角形を正確に表現することに向けて、一歩前進しました。
ここまでのプロジェクト:MyGLGame_step3-1c.zip
4. 奥に行くほど小さく描画する
三角形の前後関係は正しく描画されるようになりましたが、まだ奥の方の水色の三角形は小さく描かれていませんね。これはなぜでしょうか?
答えは、GLSLの空間においては、デプステストが有効になったとしても、Z座標はフラグメントの前後を表すためのヒントでしかないからです。-1.0〜1.0の範囲を超えた場合に表示しないようにするクリッピング処理は行われますが、大小の調整は勝手には行われず、X座標とY座標が同じフラグメントは、そのまま同じ位置にレンダリングされます。先ほど頂点シェーダを修正した時に、Z座標の値を適当に1/10にしていましたが、値が-1.0〜1.0の範囲に収まってクリッピングされないように調整できれば、1/100にしても1/1000にしても構わないのです。
Z座標の大小に応じて図形の大小を調整する、すなわち、Z座標の大小に応じてX座標とY座標を変換するためには、そのためのコードを自分で書かなければいけません。
理論的なことは後で説明するとして、まずは座標変換のためのコードを書いてみましょう。頂点シェーダ(myshader.vsh)の実装を次のように書き換えて、X座標とY座標の値をZ座標の値で割るようにするだけです。
# version 410
layout (location=0) in vec3 vertex_pos;
layout (location=1) in vec4 vertex_color;
out vec4 color;
void main()
{
gl_Position = vec4(vertex_pos.x / vertex_pos.z,
vertex_pos.y / vertex_pos.z,
vertex_pos.z / 10.0,
1.0);
color = vertex_color;
}
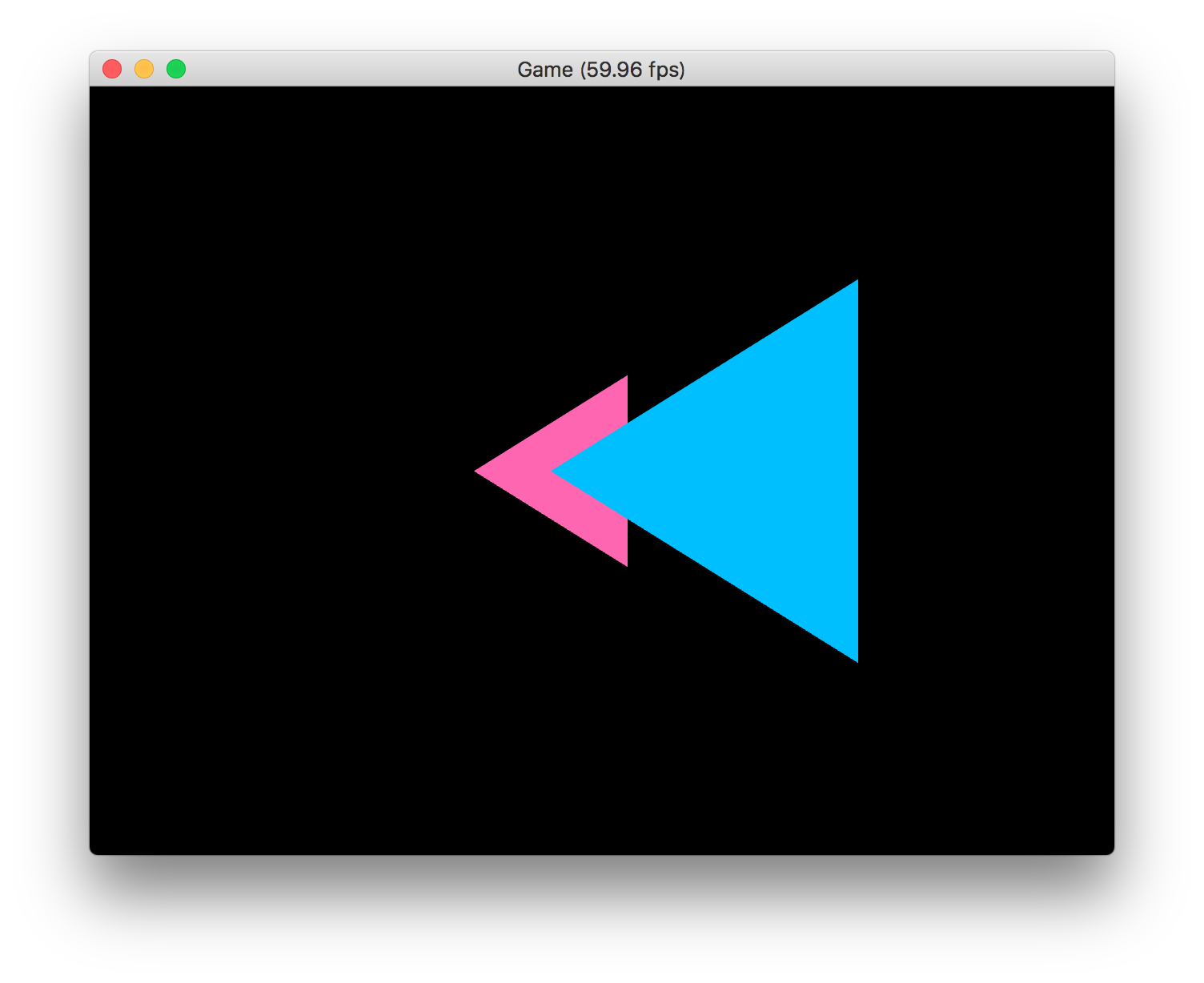
すると、次のような実行結果になります。見事に三角形の大きさが変わり、遠くにある水色の三角形が小さく表示されるようになりました!
ここまでのプロジェクト:MyGLGame_step3-1c.zip
水色の三角形が手前に来る場合も試してみましょう。ピンク色の三角形のZ座標を、1.0fから4.0fに変えてみます。
std::vector<VertexData> data;
data.push_back({ { -1.0f, 0.0f, 4.0f }, { 1.0f, 0.4f, 0.7f, 1.0f } });
data.push_back({ { 0.2f, -1.0f, 4.0f }, { 1.0f, 0.4f, 0.7f, 1.0f } });
data.push_back({ { 0.2f, 1.0f, 4.0f }, { 1.0f, 0.4f, 0.7f, 1.0f } });
data.push_back({ { -0.2f, 0.0f, 2.0f }, { 0.0f, 0.75f, 1.0f, 1.0f } });
data.push_back({ { 1.0f, -1.0f, 2.0f }, { 0.0f, 0.75f, 1.0f, 1.0f } });
data.push_back({ { 1.0f, 1.0f, 2.0f }, { 0.0f, 0.75f, 1.0f, 1.0f } });
これを実行すると、今度はピンクの三角形が奥の方に表示されるようになり、正常に三次元空間の座標変換ができていることが分かります。
ここまでのプロジェクト:MyGLGame_step3-1d.zip
5. 座標変換の理論
それでは、座標変換の理論を解説しましょう。とは言っても、実は難しいことはまったくなく、中学校で習う数学の知識があれば理解できる内容です。
座標変換は、X座標とY座標に対して行われます。Z座標はデプステストのために使われますが、それ自体の値は変化しません。
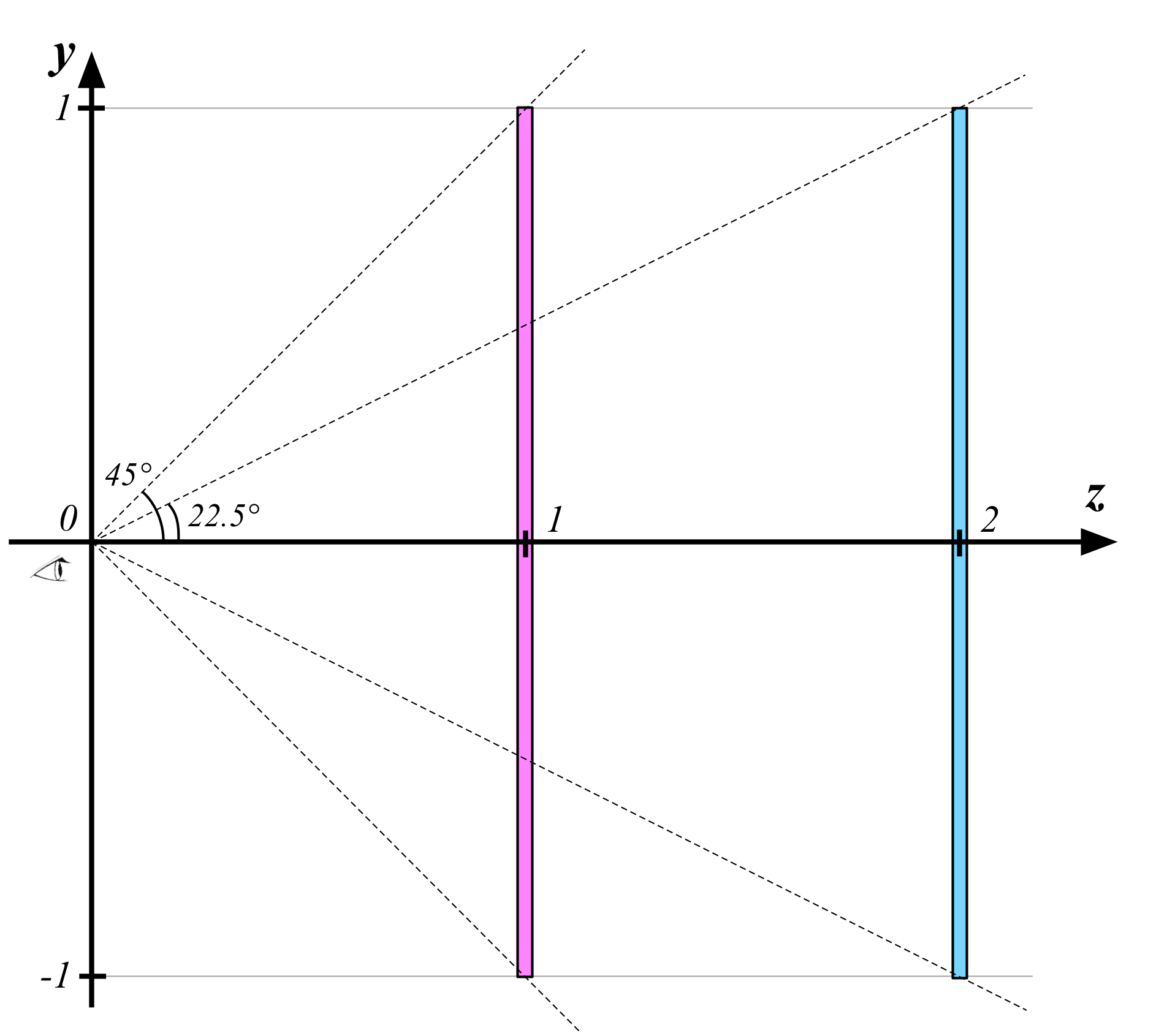
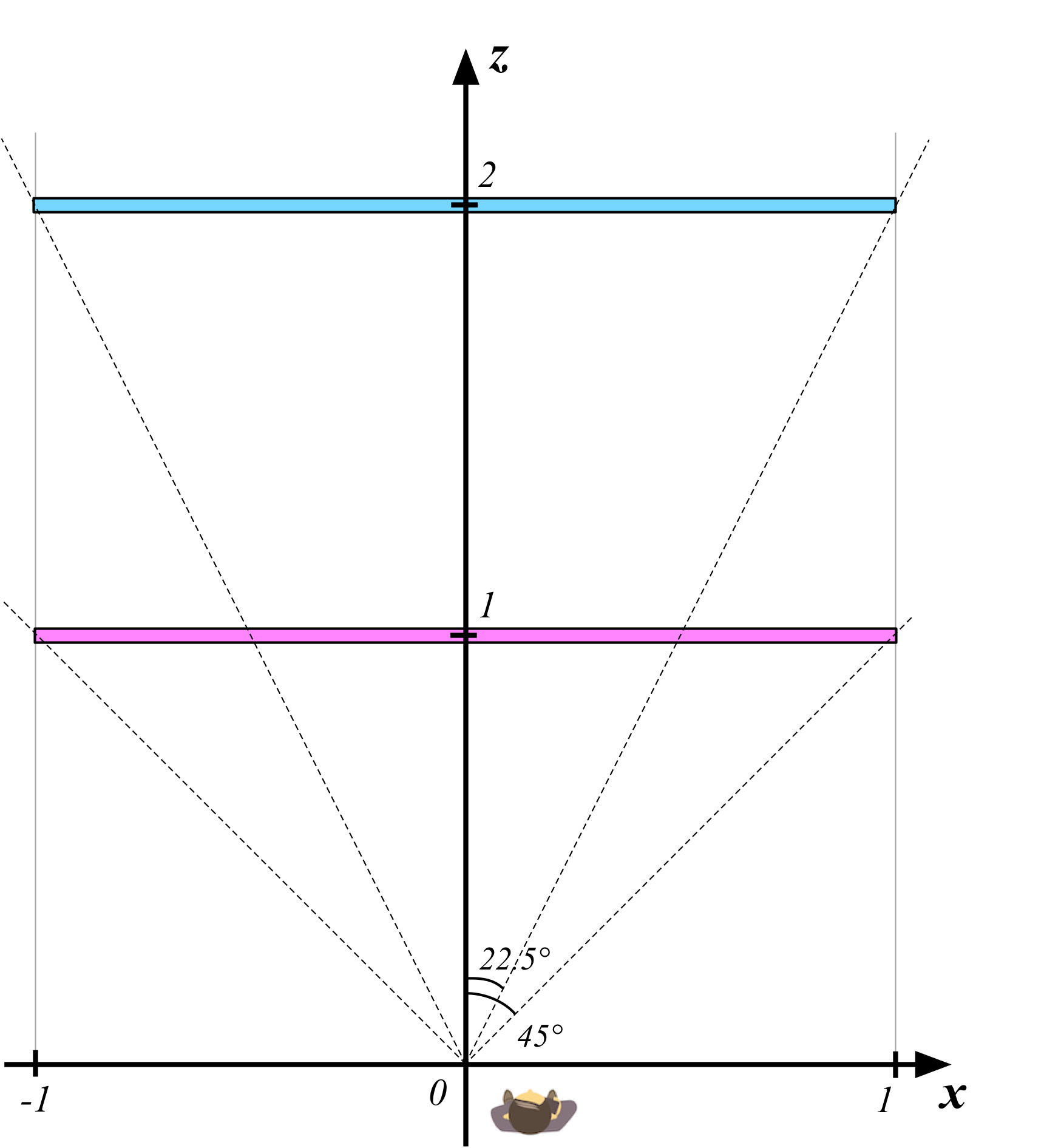
まずY座標の変換について考えてみましょう。真横から見た図を使って説明します。この図は、ピンクと水色の2つの三角形を横から見たところを表しています。三角形はそれぞれ、z=1とz=2の位置にあります。三角形はどちらもY座標の最小値が-1.0、最大値が1.0となっていますね。
基本となるカメラはz=0の位置にいて、90度の画角でZ座標の奥行方向を見ています。90度の画角ということは、上方向に45度の視野、下方向にも45度の視野が開けているということですが、つまりz=1の位置にいるピンク色の三角形の下端と上端がちょうど画面端に描画されることになるのですね。
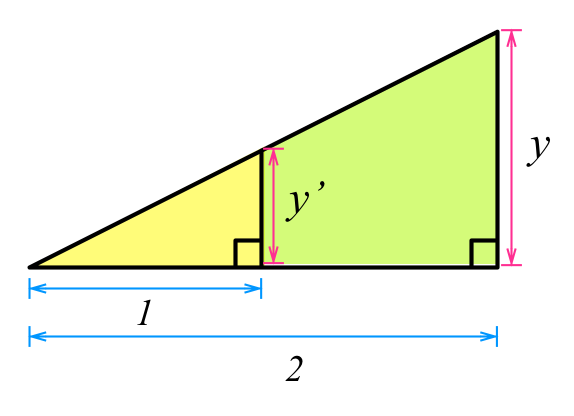
それでは、z=2の位置にいる水色の三角形の下端と上端はどうなるでしょうか? これを計算するのはとても簡単です。数学の教科書のように、次のように書き直してみると分かりやすいでしょう。
この図において、黄色い三角形と緑色の三角形は相似です。中学校の数学の知識で、我々は、相似比は底辺の長さの比であり、また三角形の高さもこの比に等しいということを知っています。すなわち、y'はyをZ=2で割った値になるということです。距離が2倍離れれば、1/2の大きさになるのです。3倍離れれば1/3の大きさに、4倍離れれば1/4の大きさになります。
つまり、カメラの位置がz=0で、基本の画角が90度だという前提の元で、奥行きを反映させたY座標の値は、単にZ座標の値で割るだけで求まるのです。
z=1の位置にあるスクリーンにオブジェクトを投影するとき、同じz=1の位置にあるオブジェクトはそのままの大きさで投影され、z=2の位置にあるオブジェクトは上端も下端も1/2の大きさで投影される、と言うこともできるでしょう。
Y座標の変換はできるようになりましたが、X座標はどうでしょうか? 実はX座標も簡単です。GLSLの空間ではX軸方向もY軸方向と同じ-1.0〜1.0の範囲になっていますので、垂直の画角と水平の画角は同一の90度です。それを真上から見ると、次の図のようになります(図が分かりやすくなるように、頂点座標は-1.0〜1.0の範囲に変更しています)。
見覚えがありますね? そう、横から見ているか上から見ているかが違うだけで、Z軸を中心とした三角形の相似比を考えるのは、X座標でもY座標でも同じことなんですね。ですので、Y座標と同じく、X座標もZ座標で割るだけで座標変換ができるのです。
なお、座標変換は色の計算には影響しませんので、フラグメント・シェーダの実装は以前のままです。
# version 410
in vec4 color;
layout (location=0) out vec4 frag_color;
void main()
{
frag_color = color;
}
ちなみに、マイナスの値でX座標やY座標の値を割ると、上下や左右がひっくり返ってしまいますので、基本のカメラに対しては、Z座標の値がz>0となる頂点データだけを考えます。
6. まとめ
今回は、X座標とY座標をZ座標の値で割っただけで三次元空間の透視座標変換ができるということを解説しました。
今回の座標変換は本当に基本的なもので、実際には画面のアスペクト比も考慮する必要がありますし、画角をいろいろな角度に変えたりする必要もあります。それにはもう少し複雑な計算が必要になります。しかしどれだけ計算が複雑になり、どれだけ繊細な3Dモデルが描画されるようになったとしても、その計算の基礎は、今回解説した通りZ座標の値でX座標とY座標を割っているだけだということを覚えておいてください。
次回は、シェーダで使われている同次座標という座標系の特徴を使って、より簡単に3Dの座標変換ができることを紹介したいと思います。