概要
本を読んで色々なことを勉強しなおし、気になったことを書くシリーズです。
今回は、アルゴリズムクイックリファレンス6章の「グラフアルゴリズム」がテーマです。
具体的には、Pythonで迷路を解く章になりました。どうしてこうなった。
迷路を解く方法について
まえおき
分岐点を節点とするグラフに変換して解く、という方法について説明されています。
それは確かにそうなのですが、「与えられた迷路をどのようにしてグラフに還元するか」という部分については、人間がやる方法のみ語られていました。
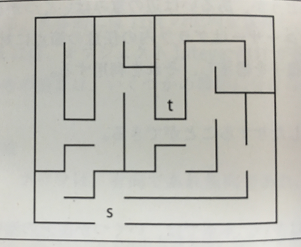
なので、迷路をできる限り書き写した、以下のような図(文字列)を入力として、グラフを作ることを考えます。
$$$$$$$$$$$$$$$$$
$ $ $ $
$ $ $ $ $ $$$$$ $
$ $ $ $ $ $ $ $
$ $ $ $$$ $ $ $ $
$ $ $ $ $ $ $
$ $ $ $ $ $ $$$$$
$ $ $ $ $t$ $ $
$ $$$ $ $$$ $ $ $
$ $ $ $ $
$ $$$ $ $$$ $ $ $
$ $ $ $ $ $
$$$ $$$$$ $$$ $ $
$ $ $ $
$ $$$ $$$$$$$$$ $
$ s $
$$$$$$$$$$$$$$$$$
非常にわかりにくいのですが、sとtというものがあり、これがスタートと目標地点に対応しています。
上の図から下の文字列を作る方法は、迷路の図の各マスとマスの間には、実はマスが隠れているものと思って、延長してつなぐという方法です。つまり、
- 下の文字列でいうところの2i行目・2j列目が、上の図でいうところのi行目・j列目と対応する
- 下の文字列におけるそれ以外の位置(たとえば3行3列の$記号)は、上の図でいうところの黒い線や、壁がない場合はマスとマスの間に隠れている「通路」と対応する
というような対応をつけることができます。
別の言い方で説明すると、格子状のマス目があったとき、碁盤の石の置き方と、将棋盤の駒の置き方と、二種類の置き方を考えることができます。
これを組み合わせて、(1)マスの中心か(2)辺の中点か(3)辺の交点か、いずれかの場所を「石や駒を置くことができる場所」と考えることにして、この「石や駒を置くことができる場所」に黒い線があれば"$"、なければ" "、という対応をさせることで得られます。
グラフをつくる
さて、前置きが長くなりましたが、この迷路からグラフを得るプログラムをPythonで書きます。
# 迷路をグラフにする:本質的に深さ優先探索
import itertools as it
def isWall(s):
return 1 if s == '$' else 0
def getWalls(arr, i, j):
return isWall(arr[i+1][j]) + isWall(arr[i-1][j]) + isWall(arr[i][j+1]) + isWall(arr[i][j-1])
def getEdge(arr, i, j, edges, v, c):
for (a,b) in zip([1,-1,0,0], [0,0,1,-1]):
if isWall(arr[i+a][j+b]) == 0:
arr[i+a][j+b] = '$'
if arr[i+2*a][j+2*b] == 0:
vn = v
cn = c + 1
else:
vn = arr[i+2*a][j+2*b]
edges.append((v, vn, c))
cn = 1
getEdge(arr, i+2*a, j+2*b, edges, vn, cn)
vs = 0
edges = list()
arr = list()
for line in open('maze_input.txt', 'r'):
arr.append(list(line))
height = len(arr)
width = len(arr[height - 1])
cellidi = range(1,width,2)
cellidj = range(1,height,2)
for i,j in it.product(cellidi, cellidj):
if getWalls(arr, i, j) == 2:
arr[i][j] = 0
elif arr[i][j] == ' ':
vs += 1
arr[i][j] = vs
# 今回のデータ用の設定
getEdge(arr, 3, 7, edges, 1, 1)
getEdgeという関数が、本質的には深さ優先探索を行っていて、ひたすら自分と隣接するマスを再帰的に処理します。マスが既に処理されたかどうかは、盤面が入っているリストarrにそのまま書き込んでいきます。
また、この処理をするときに、ついでに「辺の長さ」=「次の交差点や行き止まりに行きつくまでのマスの数」も計算することにしました。
迷路のグラフの可視化
せっかくなので、これを可視化してみます。
# 可視化
import networkx as nx
import matplotlib.pyplot as plt
import math
G = nx.Graph()
srcs, dests = zip(* [(fr, to) for (fr, to, d) in edges])
G.add_nodes_from(srcs + dests)
for (s,r,d) in edges:
G.add_edge(s, r, weight=20/math.sqrt(d))
pos = nx.spring_layout(G)
edge_labels=dict([((u,v,),d)
for u,v,d in edges])
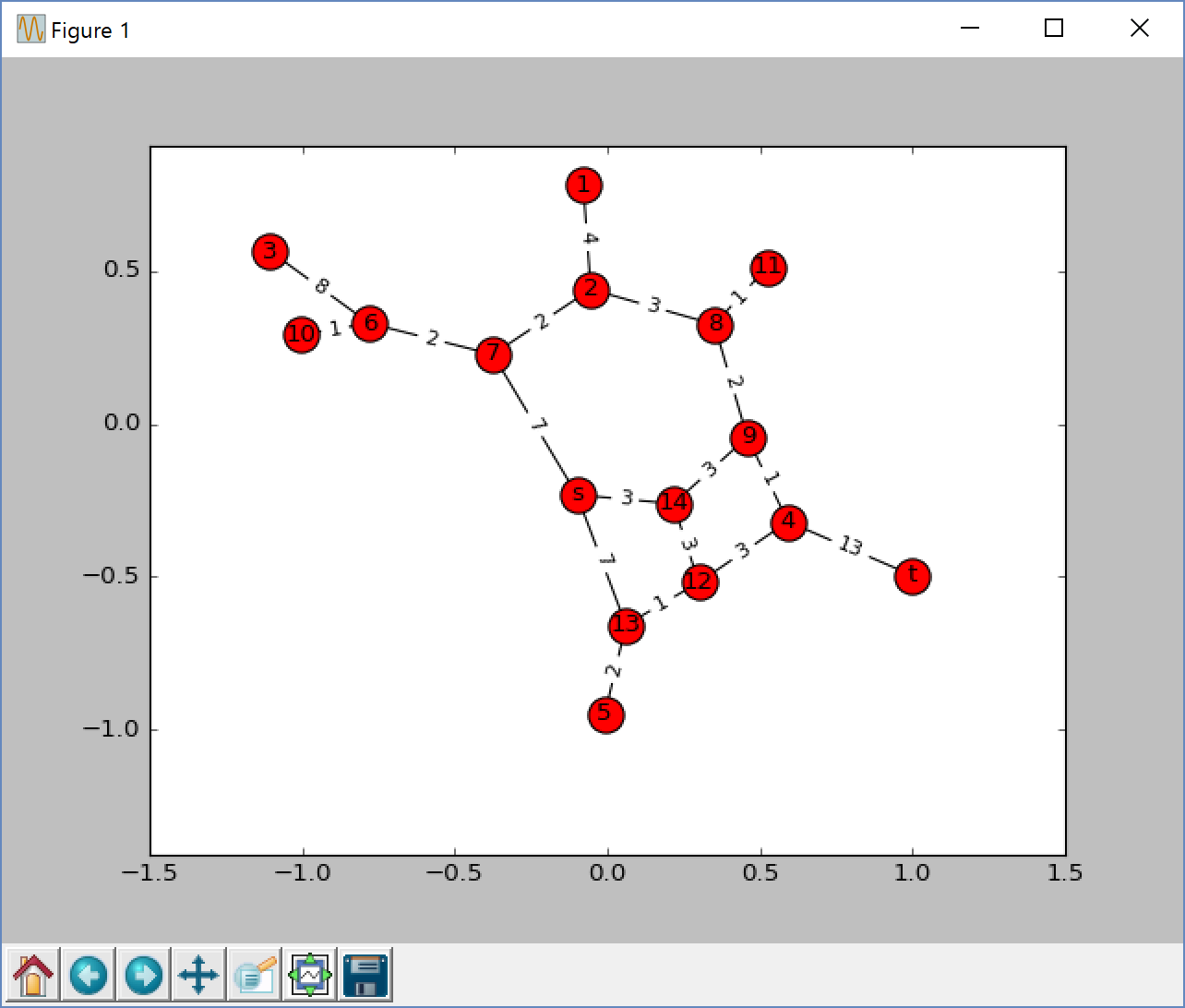
plt.figure(1)
nx.draw_networkx(G, pos, with_labels=True)
nx.draw_networkx_edge_labels(G,pos,edge_labels=edge_labels)
plt.axis('equal')
plt.show()
元の迷路と比較すると、位置関係が若干回転した感じになっていますが、sとtの位置関係をベースにつかむと、たしかに元の迷路を書き起こしたグラフになっているということがわかります。
当然ですが、本の挿絵の図とも同型になります。(頂点の名称を除いて!)
このグラフで幅優先探索
せっかくグラフが得られたので、このグラフの重みづけ(実際にかかる距離)を無視して、節点の数だけをベースに深さを計算してみます。
# 幅優先探索
import copy
# 近傍、使用済みフラグ(世代)の定義
verts = range(1,vs + 1)
verts.append('s')
verts.append('t')
neighbor = {}
used = {}
used['t'] = 0
for v in verts:
neighbor[v] = {}
used[v] = 0
used['s'] = 1
for (s, t, d) in edges:
neighbor[s][t] = d
neighbor[t][s] = d
queue = list()
queue.append('s')
while len(queue) > 0:
t = queue.pop(0)
for n in neighbor[t]:
if used[n] == 0:
used[n] = used[t] + 1
queue.append(n)
used
次のような出力が得られます。(改行を省略)
{1: 4, 2: 3, 3: 4, 4: 4, 5: 3, 6: 3, 7: 2, 8: 4, 9: 3, 10: 4,
11: 5, 12: 3, 13: 2, 14: 2, 's': 1, 't': 5}
これで、sを第1世代としたときの、各節点=交差点の「世代」がわかります。「そこに行きつくまでに、最低何回迷えばよいのか」ということの指標になる値ですね。
このグラフで最短経路の探索(ナイーブなダイクストラのアルゴリズム)
元にしている本では、有向グラフで計算していますが、無向グラフを両方向の辺のあるグラフと思うと、全く同様にダイクストラのアルゴリズムを適用できます。
ここでは、簡単に実装できるナイーブな感じのダイクストラのアルゴリズムで、sからtまでの最短距離を計算したいと思います。
# 最短コストの経路のダイクストラ法による算出
costs = {}
# costs[v] = (cost, prev, used)の組
for v in verts:
costs[v] = (float("inf"),0,0)
costs['s'] = (0,-1,0)
queue = list()
queue.append('s')
while len(queue) > 0:
t = queue.pop(0)
costs[t] = (costs[t][0], costs[t][1], 1)
for n in neighbor[t]:
if costs[n][2] == 0 and costs[n][0] > neighbor[t][n] + costs[t][0]:
costs[n] = (neighbor[t][n] + costs[t][0], t, 0)
# queueへの入れ方を工夫すればもっと早くなるが、ここではqueueには最低の値を一つ入れるだけにする
mincost = float("inf")
minv = 's'
for v in verts:
if mincost > costs[v][0] and costs[v][2] == 0:
mincost = costs[v][0]
minv = v
if minv != 's':
queue.append(minv)
{1: (13, 2, 1),
2: (9, 7, 1),
3: (17, 6, 1),
4: (7, 9, 1),
5: (9, 13, 1),
6: (9, 7, 1),
7: (7, 's', 1),
8: (8, 9, 1),
9: (6, 14, 1),
10: (10, 6, 1),
11: (9, 8, 1),
12: (6, 14, 1),
13: (7, 's', 1),
14: (3, 's', 1),
's': (0, -1, 1),
't': (20, 4, 1)}
queueのあたりが相当適当な実装ですが、処理するたびにコストが最低の頂点を一つだけappendするので、正しい結果を返します。出力された結果は、例えば't'の行を見ると(20, 4, 1)となっていますが、ゴールするまでの距離(歩数)が20で、ひとつ前の交差点が"4"で表されている場所である、ということを意味しています。
これをたどることで、距離だけではなく最短経路そのものもわかります。めでたしめでたし。
ちなみに、この記事を書くにあたってはじめて真面目にPythonを使ってみて、次のようなことを思いました。
- タプルを使えるのは相当楽
- タプルへのアクセスを[0]とか[2]とかでやるのはとても雑(Pythonが悪いとかいうことではない)
forでの組み合わせとかではなくて、適当な構造体もどきみたいな使い方をするときは、やはり構造体的な何かとしてきちんと定義すべきなのかな、ということを思いました。
おしまい
その他のアルゴリズムについては、とりあえず割愛します。このグラフについてフロイド・ワーシャル法を適用したり、プリム法を適用したり、というのもできますが、7章や8章に時間を使ってから、余裕があれば考えた方がよいかと思いました。
ちなみに、このシリーズには、他に次のような記事があります。
バケツソートとn log nの壁 - アルゴリズムクイックリファレンス4章の補足 - ※Ruby
探索と計算の分割 - アルゴリズムクイックリファレンス5章の補足 - ※Python
【この記事→】Pythonで迷路を解く - アルゴリズムクイックリファレンス6章の補足 - ※Python
フォード・ファルカーソン法とその応用 - アルゴリズムクイックリファレンス8章の補足 - ※Python