概要
本を読んで色々なことを勉強しなおし、気になったことを書くシリーズです。
今回は、アルゴリズムクイックリファレンス8章の「ネットワークフローアルゴリズム」がテーマです。
全体的に、フォード・ファルカーソン法はすごい、という感じですね。
本編1:フォード・ファルカーソン法の概要
グラフ上の様々な量について
(有向)グラフ上の辺に、しばしば重み付けをします。
この重みの量は、
- 時間や距離であったり、
- コストであったり、
- 何らかの流量であったり、
様々な概念に対応するものですが、いずれも同じ「辺の重みづけ」として定式化されます。
この重みの量を時間や距離ととらえて、「あるスタート地点からゴール地点に向かうまでにかかる時間や距離はどれぐらいになるか」ということに対応する計算を行う方法については、6章のダイクストラ法にて考えています。
この章では、上の例に記したコストや流量についての考察をします。
フォード・ファルカーソン法とそのポイント
まず、流量=フローについて考えます。フォード・ファルカーソン法としてよく知られる方法があります。増加道を貪欲に増やしていく、という発想自体は、比較的分かりやすいと思いますが、重要なポイントは「通常の向きと反対の向きの流れも考える」ということだと思います。ここでは、その考え方を重点とした説明を試みます。
分かりやすくするために、どの辺も重みが1の次のような図のグラフを考えて、このグラフのSからTまでの最大フローを求めることを考えます。
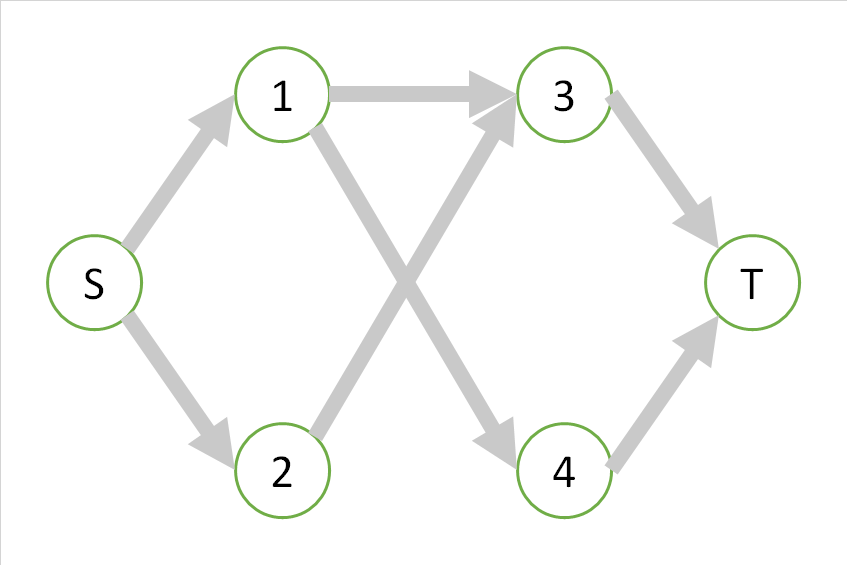
このグラフでは、SからTまでは次の3つの経路が存在し、かつこの経路のみですべての経路が尽きます。
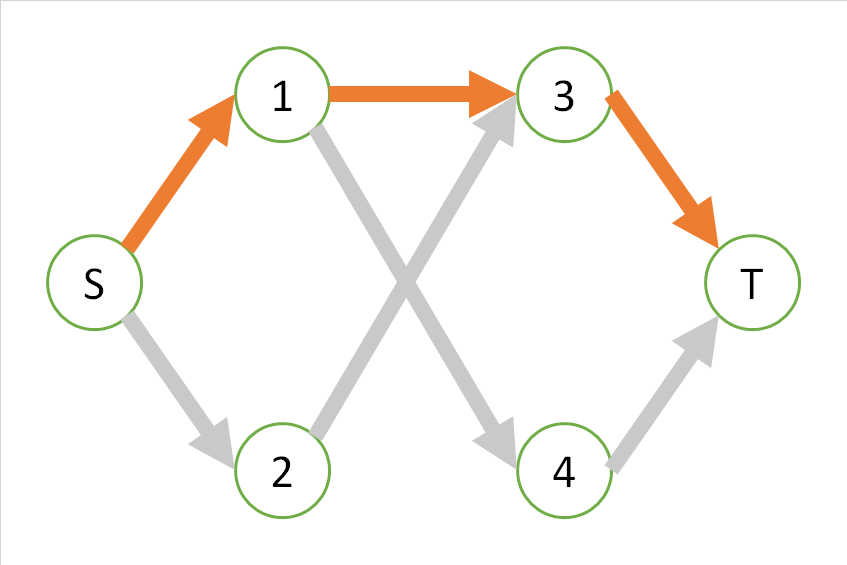
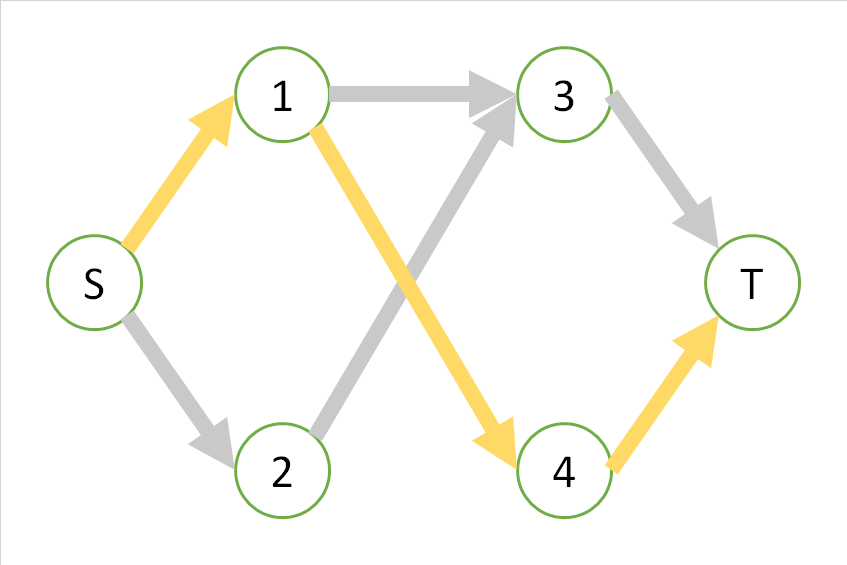

とりあえず、最初のオレンジの経路を見ると、この経路は黄色や青の経路と同時に用いることはできません。その意味で、オレンジの経路ひとつをとると、「オレンジの経路にさらに並行する経路を付け加えることでは」これ以上フローを増やせないような状態になり、フローは「極大」であるように思われます。
一方で、黄色の経路と青色の経路は同時に取れますから、黄色の経路だけ、あるいは青色の経路だけをとっても、それらは「極大」ではなく、黄色と青色を同時に取った経路は「極大」であるように思えます。そして、この場合は同時に取り得る最大のフローでもあります。
一般に、貪欲なアルゴリズムは適当な極大値にはまってしまうような場合もあり得ますが、フォード・ファルカーソン法においては、これを「逆向きを含むフロー」を考えることで解消しています。
つまり、次のような経路が存在している、と考えるわけです。
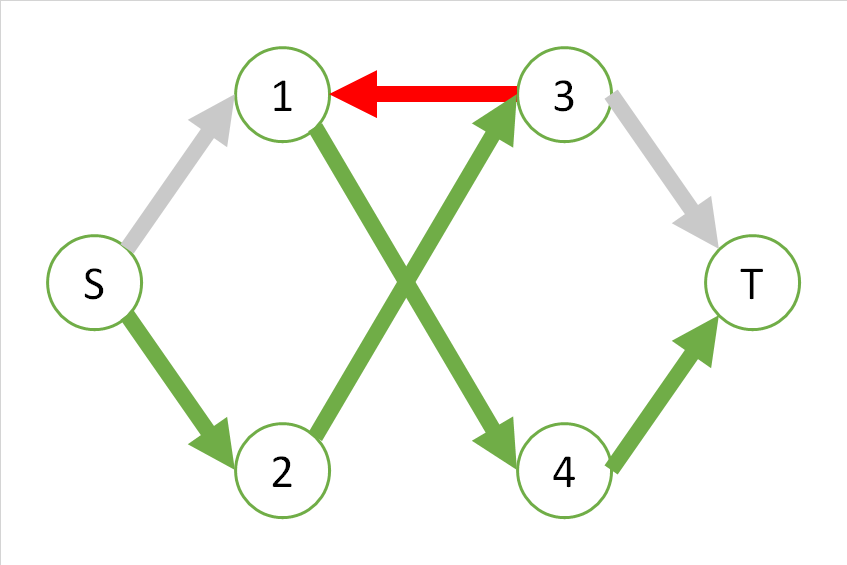
3から1の辺は、元のグラフには存在しておらず、1から3の辺のみ存在しているので色を変えています。この3から1の辺を$e_{31}$と書くと、$e_{31}=-e_{13}$ということになります。
この経路を含めて考えると、もはやオレンジの経路は極大ではなく、次のようなフローを考えることができるようになります。
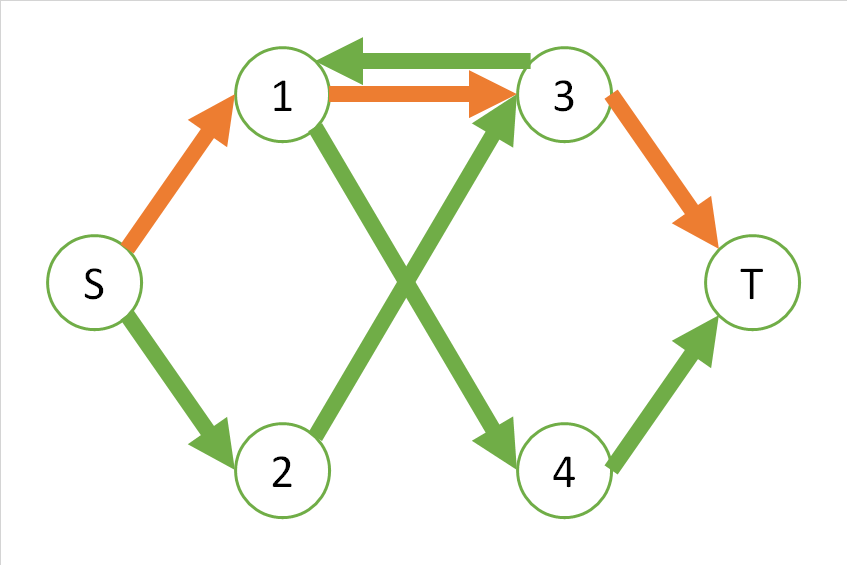
この図の1と3の間の辺は、結局打ち消しあって、使っていないのと同じになります。
今の例の3から1の辺のように、"虚道"みたいなものを考えると、変な極大値にはまらずに済みます。と言っても、はまらないことは自明ではないので、中々びっくりする主張だと思います。証明は比較的易しいものの。
ここまで述べてきたことは、
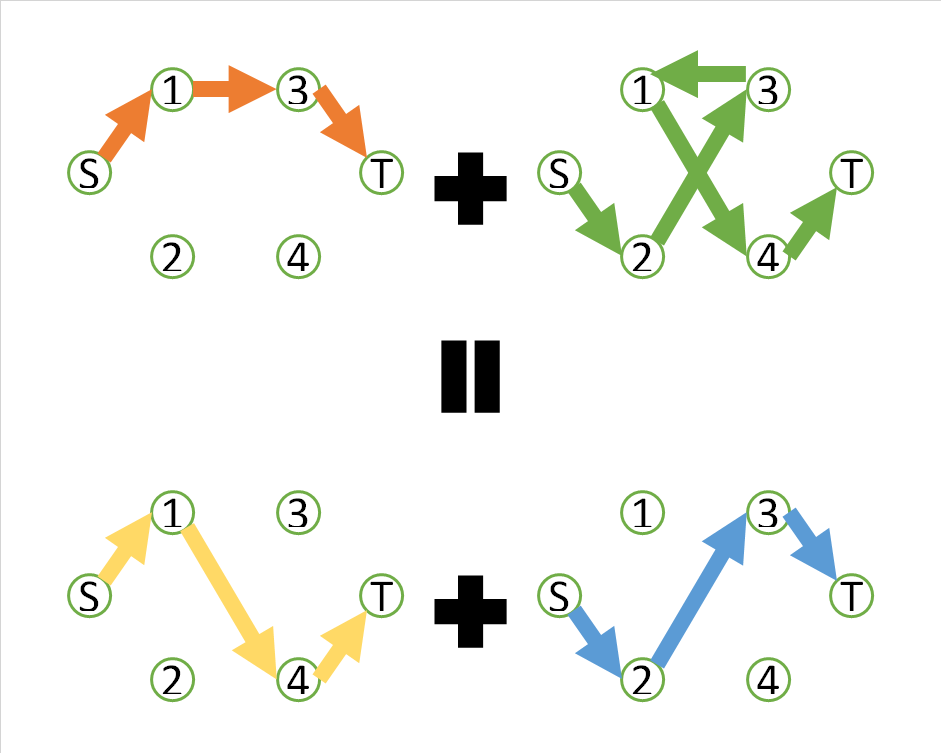
というようなことでもあります。そして、フォード・ファルカーソン法によれば、「実在する」3つの経路のどれをスタート地点として取ったとしても、増加道をとれば必ずこの等式の左辺か右辺に至る、という意味のことを言っています。(もちろん、このグラフだけではなく、一般のグラフにおいて、同じ意味の性質が成り立つと言っています。)
これは中々強い数学的性質で、非常に興味深いと思います。
実際、これらの経路の取り方について、
- 深さ優先で取ることにすれば、当初のフォード・ファルカーソン法
- 幅優先で取ることにすれば、エドモンズ・カープ法
- コスト優先で取ることにすれば、最小コストフロー問題の解法であるプライマル・デュアル法
という類似のアルゴリズムを得ることができます。その背後には、ここで見たように、最大フローを上記のような経路たちの線形結合(足し算)と思えるという事実が潜んでいたりします。
改めて、フォード・ファルカーソン法(の一般化)をざっくりと数学の言葉で説明すると、
- 矢印の向きを逆にした経路も含めて、SからTまでのすべての経路を洗い出す。この例の場合は$e_{s1}+e_{13}+e_{3t}, e_{s2}+e_{23}-e_{13}+e_{14}+e_{4t}, e_{s1}+e_{14}+e_{4t}, e_{s2}+e_{23}+e_{3t}$
- これらの経路ひとつひとつについて、流量を1として次のような等式を作る。この例の場合は
$$\begin{align}+e_{s1}&&+e_{13}&&+e_{3t}&= 1 \\
&+e_{s2}+e_{23}&-e_{13}&+e_{14}+e_{4t}&&= 1 \\
+e_{s1}&&&+e_{14}+e_{4t}&&= 1 \\
&+e_{s2}+e_{23}&&&+e_{3t}&= 1
\end{align}$$ - この条件で、これらの線形結合の和の最大値を求めたい。制約条件は、$e_{xy}$の係数を$a_{xy}$として、$0 \leq a_{xy}\leq$(各辺の最大フロー)
- 実際に$a_{xy}$たちを求めるために、制約条件を満たす等式を片っ端から足していく
- 足し方によらず最大値にたどり着くが、計算の速さやコストなどの条件に応じて足し方を変える
ということになります。
本編2:Pythonによる最小コストフローの計算の実装
問題設定
さて、上記の流量に加えて、各辺に対してコストが定義されている場合があります。このとき、SからTまで、流量$x$を確保しつつ、できるだけ小さいコストにしたい、という場合があります。
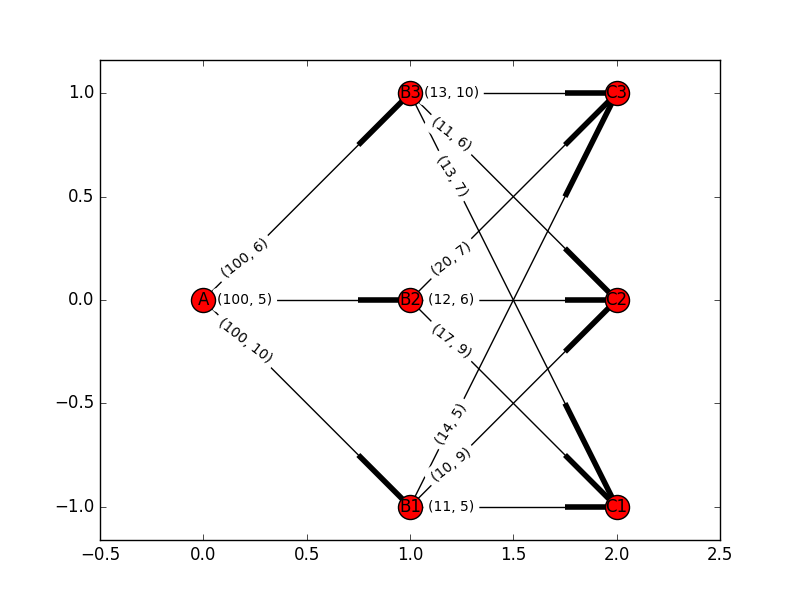
例えば、一次工場$A$で生産した品物を、二次工場$B_1,B_2,B_3$で加工して、店舗$C_1,C_2,C_3$に蓄えることを考えます。
具体的には、次のような流量とコストを持っているものとします。
※(from頂点,to頂点(流量,コスト))の形式
edges = {('A', 'B1', (100, 10)),
('A', 'B2', (100, 5)),
('A', 'B3', (100, 6)),
('B1', 'C1', (11, 5)),
('B1', 'C2', (10, 9)),
('B1', 'C3', (14, 5)),
('B2', 'C1', (17, 9)),
('B2', 'C2', (12, 6)),
('B2', 'C3', (20, 7)),
('B3', 'C1', (13, 7)),
('B3', 'C2', (11, 6)),
('B3', 'C3', (13, 10))}
この条件下で、$A$からの流量の合計が$100$となるようにして、できる限りコストが小さくなるようにすることを考えます。
単一ソース・シンクの問題への帰着と、制限の追加
そもそも、フォード・ファルカーソン法が通用する問題であることを明確にするために、グラフの形式を少し変換します。
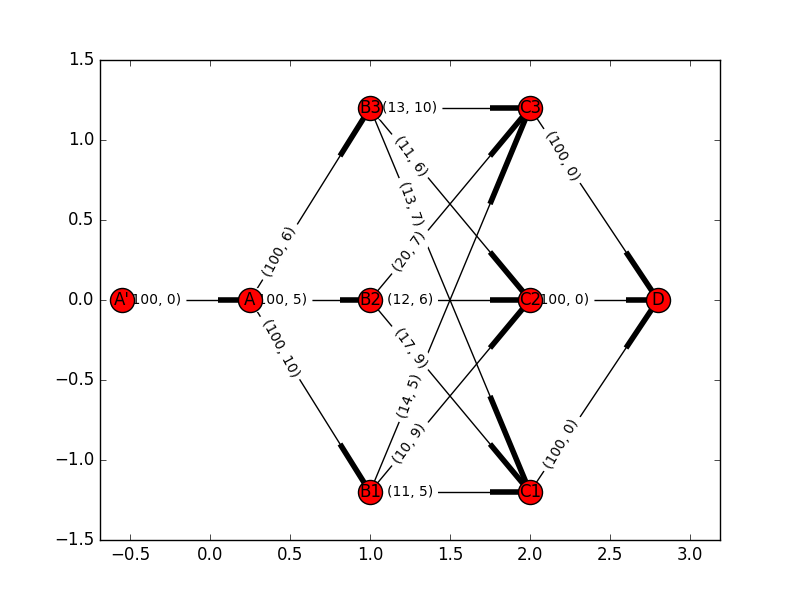
シンクの追加
これは本当に形式的な問題ですが、$C_1,C_2,C_3$の先に$D$という点を追加します。これは、これまでの説明でいうところのTにあたります。$C_i$から$D$への辺は、一律で$(100,0)$としておきます。これが、問題に本質的な影響を与えないのは明らかです。
ソースの追加
さて、この問題について直ちにフォード・ファルカーソン法を適用すると、単純な最大流量が求まってしまい、流量の合計$=100$よりも過剰なコストを計算してしまいます。
そこで、$A$の前に$A'$という頂点を追加します。$A'$から$A$への辺は$(100,0)$としておきます。
この条件下で、最大流量を求めると、(元々のグラフの最大流量が$100$を超えている前提で)流量の合計$=100$という制限に対応するのは明らかです。実際、元々のグラフの最大流量は$121$になるので、この条件で問題ありません。
再描画
解く
そこまで性能を意識せずに、とりあえず解けるものを作ります。
edges = {("A'", 'A', (100, 0)),
('A', 'B1', (100, 10)),('A', 'B2', (100, 5)),('A', 'B3', (100, 6)),
('B1', 'C1', (11, 5)),('B1', 'C2', (10, 9)),('B1', 'C3', (14, 5)),
('B2', 'C1', (17, 9)),('B2', 'C2', (12, 6)),('B2', 'C3', (20, 7)),
('B3', 'C1', (13, 7)),('B3', 'C2', (11, 6)),('B3', 'C3', (13, 10)),
('C1', 'D', (100, 0)),('C2', 'D', (100, 0)),('C3', 'D', (100, 0))}
# パスの一覧を取得する…結果はコスト、辺のリスト、係数のリスト
def getAllPath(edges, visited, f, t, r, c, e, a):
if f == t:
r.append((c,e,a))
for k in neighbor[f].keys():
if k not in visited:
getAllPath(edges, visited + [f], k, t, r, c + neighbor[f][k][2], e + [neighbor[f][k][1]], a + [neighbor[f][k][0]])
# パスに対して「今そのパスが取れる最大の値」を返す
def getMaximalFlow(world, (c,e,a)):
l = len(e)
delta = float("inf")
for i in range(0, l):
if a[i] > 0:
if delta > world[e[i]][0] - world[e[i]][1]:
delta = world[e[i]][0] - world[e[i]][1]
elif a[i] < 0:
if delta > world[e[i]][1]:
delta = world[e[i]][1]
else:
delta = 0
return delta
# グラフを更新する
def updateWorld(world, (c,e,a), delta):
l = len(e)
for i in range(0, l):
world[e[i]] = (world[e[i]][0], world[e[i]][1] + a[i] * delta)
変数の名前はかなり適当です。ちなみに、ファイルを分けていますが、実際にはipython notebook(jupyter)の中の別のチャンクで実行しています。(つまり、変数等は引き継がれている状態)
neighbor = {}
world = {}
for (f,t,(v,c)) in edges:
# コスト用辞書
if not f in neighbor.keys():
neighbor[f] = {}
neighbor[f][t] = (1,(f,t),c) # 重み係数、基底、コスト
if not t in neighbor.keys():
neighbor[t] = {}
neighbor[t][f] = (-1,(f,t),-c) # 重み係数、基底、コスト
# 現在値格納用辞書
world[(f,t)] = (v,0) # 最大値、現在値
r = []
getAllPath(edges,[],"A'",'D',r,0,[],[])
r.sort()
l = len(r)
i = 0
while i < l:
delta = getMaximalFlow(world, r[i])
if delta > 0:
updateWorld(world, r[i], delta)
i = 0
else:
i = i + 1
world
{('A', 'B1'): (100, 25), ('A', 'B2'): (100, 49), ('A', 'B3'): (100, 26),
("A'", 'A'): (100, 100),
('B1', 'C1'): (11, 11), ('B1', 'C2'): (10, 0), ('B1', 'C3'): (14, 14),
('B2', 'C1'): (17, 17), ('B2', 'C2'): (12, 12), ('B2', 'C3'): (20, 20),
('B3', 'C1'): (13, 13), ('B3', 'C2'): (11, 11), ('B3', 'C3'): (13, 2),
('C1', 'D'): (100, 41), ('C2', 'D'): (100, 23), ('C3', 'D'): (100, 36)}
ちょっとわかりにくいかもしれません。可視化するとこんな感じです。一部切れていますが。
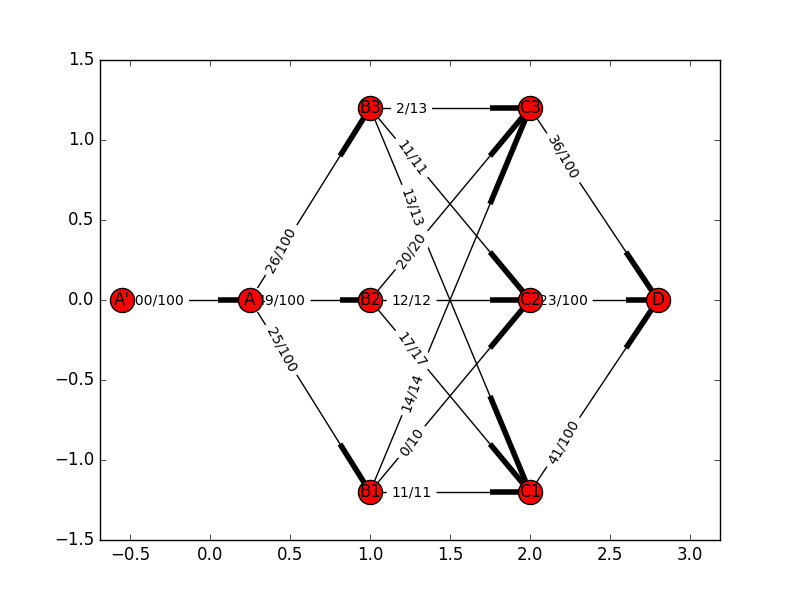
簡単な検算方法としては、$B_3\to C_3$が$2/13$、$B_1\to C_2$が$0/10$となっていますが、これはまさにコストが高い道なので、計算自体は合っています。
速度評価をするとすれば、Python(Networkx)が持っているSolverなんかと比較すればよいのかと思いますが、基本的には勉強が目的なので、ガッチリ比較は劣後とします。
その他補足
帰着に関するポイント
「現在のグラフに無い点や辺を付け加える」というのは、グラフ関係で別の問題への帰着に用いる常套手段です。わかりやすいところだと、無向グラフを有向グラフに変換するとか、先頭に新しいノードとエッジを加えるとか、末尾に新しいノードとエッジを加えるとか、そういうところです。
他にも、ノードを二つに分割するとか、そういう手法もあります。(今回でいえば、$A`$なんかは新しい点を加えるというよりはノードの分割に近いかと思います)
描画用のコード
# 可視化
import networkx as nx
import matplotlib.pyplot as plt
import math
G = nx.DiGraph()
srcs, dests = zip(* [(fr, to) for (fr, to) in world.keys()])
G.add_nodes_from(srcs + dests)
for (s,r,(d,c)) in edges:
G.add_edge(s, r, weight=20/math.sqrt(d))
# 位置、微調整する
pos = {"A'" : ([-0.55,0]),
'A' : ([0.25,0]),
'B1' : ([1,-1.2]),
'B2' : ([1,0]),
'B3' : ([1,1.2]),
'C1' : ([2,-1.2]),
'C2' : ([2,0]),
'C3' : ([2,1.2]),
'D' : ([2.8,0]),
}
edge_labels=dict([((f,t,),str(world[(f,t)][1]) + '/' + str(world[(f,t)][0]) )
for (f,t) in world.keys()]) # 辺のラベル、適当に変える
plt.figure(1)
nx.draw_networkx(G, pos, with_labels=True)
nx.draw_networkx_edge_labels(G,pos,edge_labels=edge_labels,label_pos=0.74) # これも適当に調整
plt.axis('equal')
plt.show()
おしまい
次はA*ですかね。7章もPythonかなー。
ちなみに、このシリーズには、他に次のような記事があります。
バケツソートとn log nの壁 - アルゴリズムクイックリファレンス4章の補足 - ※Ruby
探索と計算の分割 - アルゴリズムクイックリファレンス5章の補足 - ※Python
Pythonで迷路を解く - アルゴリズムクイックリファレンス6章の補足 - ※Python
【この記事→】フォード・ファルカーソン法とその応用 - アルゴリズムクイックリファレンス8章の補足 - ※Python