１．はじめに
さて、前回までのアルゴリズムで基本的なことはできるのですが、もう一歩進むため、今回は先にアルゴリズムを説明します。
２．やりたいこと
其の７や、其の８のアルゴリズムで得た閉領域が２つあります。
１つは、切られる側とします。（以降の絵では赤枠）
もう一つは、切る側とします。（以降の絵では青枠）
切られる側の領域から切る側の領域を切り抜き新たな閉領域を求める（アルゴリズム（考え方）を示します。）。
３．考え方
２つの閉領域の重なり具合により判断します。
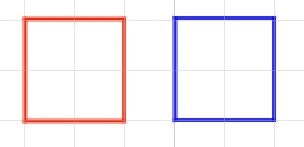
３．１ 領域が重ならない
この場合、重なる領域は無しと判断します。
- 重なりの有無は、赤枠の全頂点が青枠内か否かを判断する。
- ある点が領域内か否かを判断するには別のアルゴリズムが必要なのですが、機会があれば別途説明したいと思います。
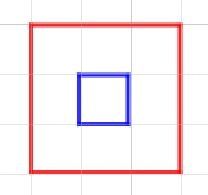
３．２ 切る側が切られる側の内部に収まる
この場合、切る側（青枠）の領域と同じと判断します。
- 青枠の全頂点が赤枠内であるか判断します。
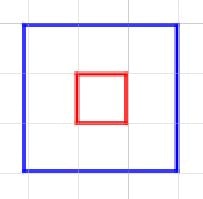
３．３ 切られる側が切る側の内部に収まる
この場合、切られる側（赤枠）の領域と同じと判断します。
- 赤枠の全頂点が青枠内であるか判断します。
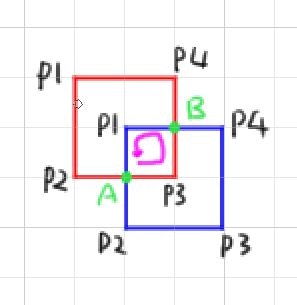
３．４ 双方の領域が一部重なる
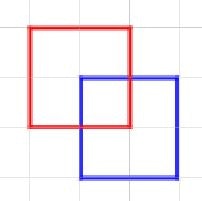
この場合、３．１～３．３に当てはまりません。
この場合、双方とも、一部頂点は相手の領域内で他の頂点が領域外となります。
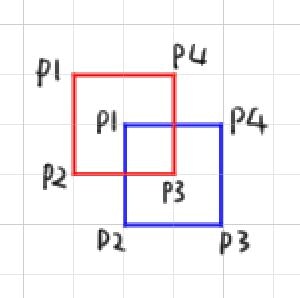
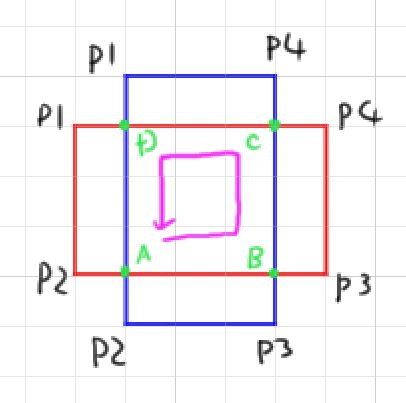
この条件の場合、赤枠の全稜線について、青枠の全稜線と交差チェックし、交点を求めます。
※赤P1-P2と青P1-P2/P2-P3/P3-P4/P4-P1 のように
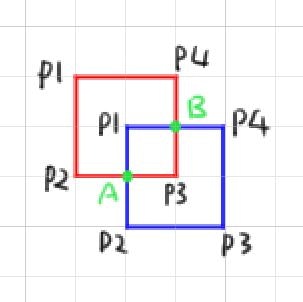
これにより、新たなA/Bの２点が求められます。この交点A/Bは各閉領域上どの位置（順番）かも保持します。
赤枠の場合、P1,P2,A,P3,B,P4,P1
青枠の場合、P1,A,P2,P3,P4,B,P1
- 赤枠の最初の点から、最初に見つかった交点まで照査します。（交点Aを新閉領域として保持）
- 赤枠を次の交点まで照査します。（P3,交点Bを新閉領域として保持）
- 青枠を当該交点(B)から次の交点まで照査します。（P1,交点Aを新閉領域として保持）
- 最初の交点に戻ったので終了。 これにより、A,赤P3,B,青P1,Aという閉領域が求められました。
３．５ 切られる側が切る側により分断される。
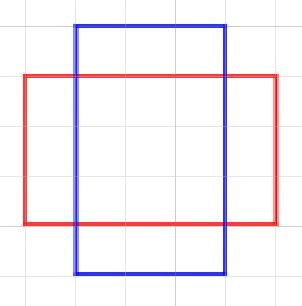
この場合、３．１に近く（頂点と相手閉領域の関係）、３．２～３．４に当てはまりません。
しかし、双方の稜線の交差チェックをすると交差点があります。（３．１は交差点がない）
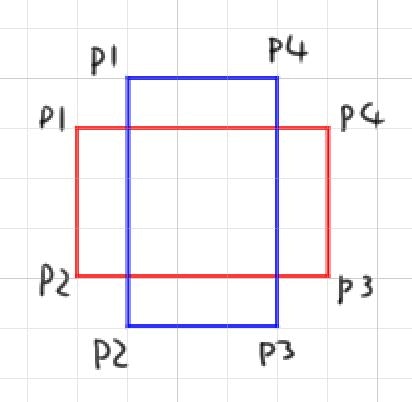
この条件の場合、赤枠の全稜線について、青枠の全稜線と交差チェックし、交点を求めます。
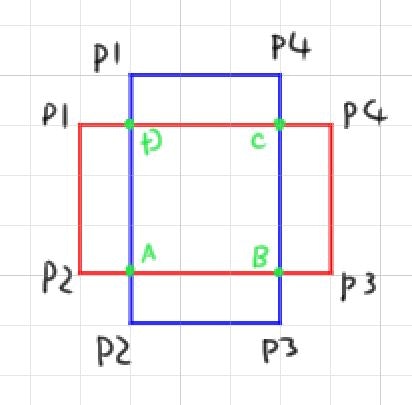
これにより、新たなA/B/C/Dの４点が求められます。この交点A/B/C/Dは各閉領域上どの位置（順番）かも保持します。
赤枠の場合、P1,P2,A,B,P3,P4,C,D,P1
青枠の場合、P1,D,A,P2,P3,B,C,P4,P1
- 赤枠の最初の点から、最初に見つかった交点まで照査します。（交点Aを新閉領域として保持）
- 赤枠を次の交点まで照査します。（交点Bを新閉領域として保持）
- 青枠を当該交点(B)から次の交点まで照査します。（交点Cを新閉領域として保持）
- 赤枠を当該交点(C)から次の交点まで照査します。（交点Dを新閉領域として保持）
- 青枠を当該交点(D)から次の交点まで照査します。（交点Aを新閉領域として保持）
- 最初の交点に戻ったので終了。
これにより、A,B,C,D,Aという閉領域が求められました。
- 実は３．４と同じ処理です。3,4が繰り返し部分。
４．おわりに
今回の説明では、簡単な閉領域の例でしたが、実際の閉領域は複雑な多角形です。
よって現状のようなアルゴリズムになっています。（実際はもっと複雑ですが）
なお、本アルゴリズムはこの後いろいろな場面で利用します。