１．はじめに
今回は、 其の７で求めたスライス面（閉領域）から出力結果となる要素を求めていく第１弾になります。
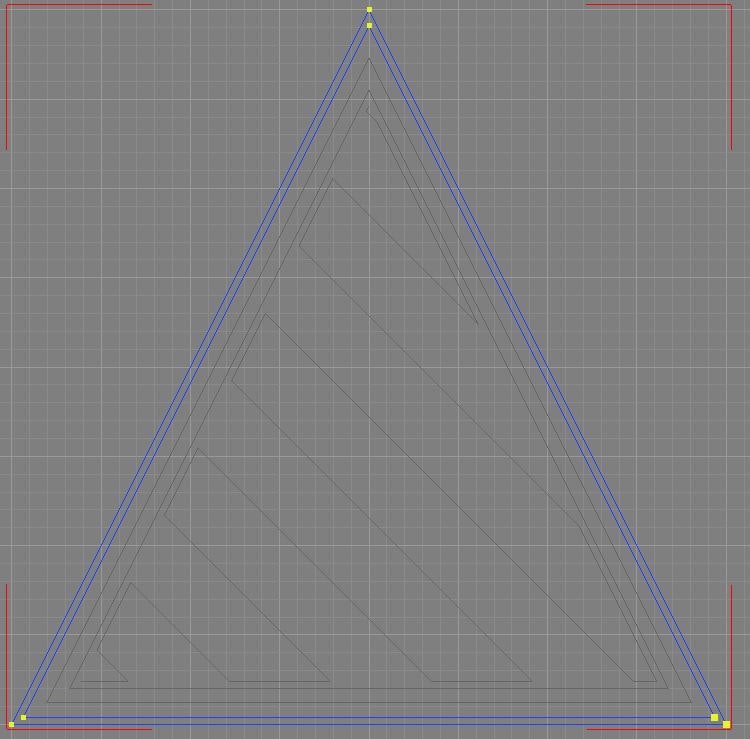
まずは、モデルの輪郭となる外周を求めます。このとき利用するのが閉領域の縮小アルゴリズムになります。
2．求めるもの
求める結果（数値）は３Ｄプリンタのノズルが通過する場所です。
ノズルには一般的（？）に0.4[mm]など穴が開いていてそこからフィラメントが溶け出し、0.4[mm]径の樹脂で線を引き、それを繋ぎ合わせて立体化します。このため、ノズルの通過する線は出力する線の中心となります。
つまり、其の７で求めた閉領域はモデルの輪郭ではあるが、外周部分のノズルが通る線ではないのです。わずか（ノズル径の半分）に内側である必要があります。
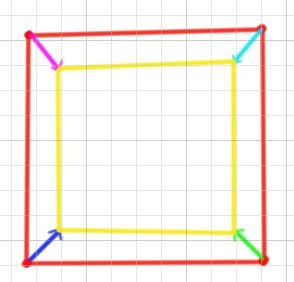
概念は以下のようになります。（外側がスライスした閉領域。内側が求める閉領域）
三角形状の場合
四角形状の場合
実際はもっと複雑な形状．．．（簡単な方）
３．基本的な考え方（ボツ）
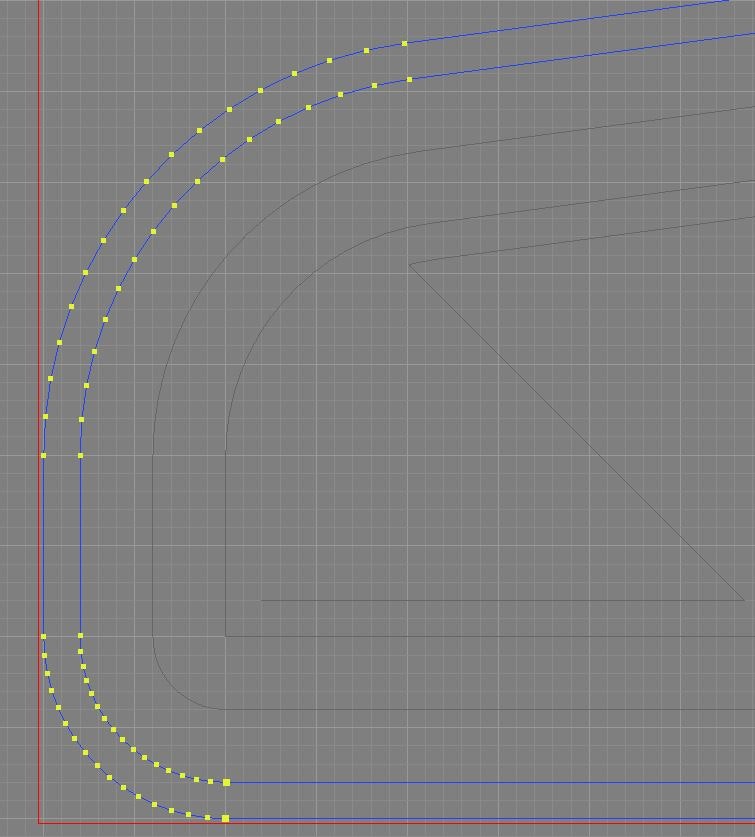
各稜線を法線と反対方向へ所定量移動し、隣接の稜線との交点を新たな点として構成することにより縮小された閉領域を求める。
この方法は、縮小したい量に対し元となる閉領域が十分に大きい場合は問題無かったのですが、複雑な形状を試すうち破綻する場面が出てきたためボツにしました。
４．基本的な考え方
各頂点を隣接稜線から得られるベクトルの和方向へ移動させ、問題なければ、新規頂点郡で構成される閉領域を生成する方式にしました。
これは、前記ボツとなった考え方の問題解決のため、現在採用している方法です。（でも、凄く時間的コストがかかるため改良が必要と思っています）
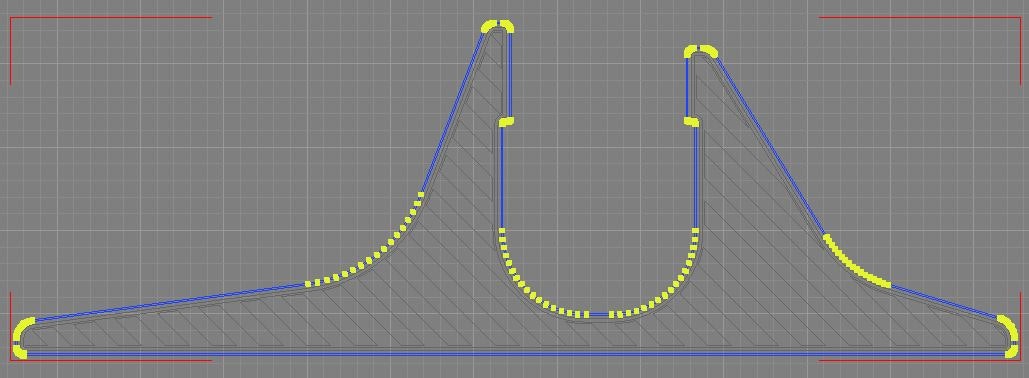
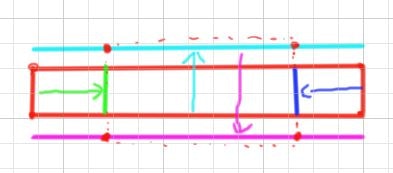
横方向には十分縮小できるが、縦方向には十分な領域が無い以下の場合、ボツアルゴリズムでは、失敗までは分かるが最適解を求めるのにさらに考える必要がありました。
採用しているアルゴリズムでは、移動用のベクトルから交差点を求め、最適解を求められるため、現状採用しています。
※最適解が人により，考えにより異なると思います。
※ここでは、閉領域が１本の線になります。
５．おわりに
今回得られた閉領域は、モデルの輪郭を表す外周情報になります。実際にG-Codeとして出力するのは別の機会に。
また、ここでの閉領域の縮小アルゴリズムは、外周に対しノズル径さらに縮小すると内周情報になります。内周は０～の本数あるため、パラメータに従い繰り返し、最後の内周（または外周）からノズル径の半分縮めるとインフィルを構成する閉領域情報となります。ここまでは本アルゴリズムで実施できます。
インフィルについては次回。