１．はじめに
今回は、スライサーソフトのアルゴリズムについてです。
まずは、３Ｄモデルデータを”スライス”（輪切り）にするためのアルゴリズムです。
私は、最初にこの点を考えつくまでが時間がかかりました。
多分何処かに、良いライブラリとして転がっているのではないかと思います。
- 本来だと、順番的には３Ｄモデルデータの読み込みだと思いますが、ＳＴＬファイルのフォーマットについては、ググると出てきます。（日本語で！！）
- フォーマットさえ分かれば、あとはデータを読み込み，内部で効率よく管理するのみですので、時間があるときにまとめたいと思います。
2．スライス（輪切り）
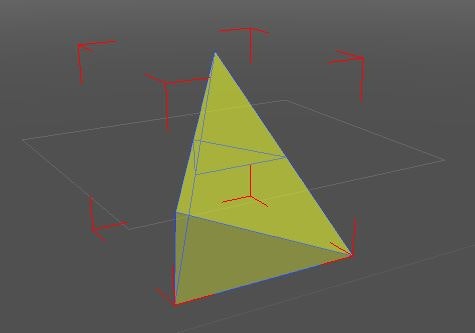
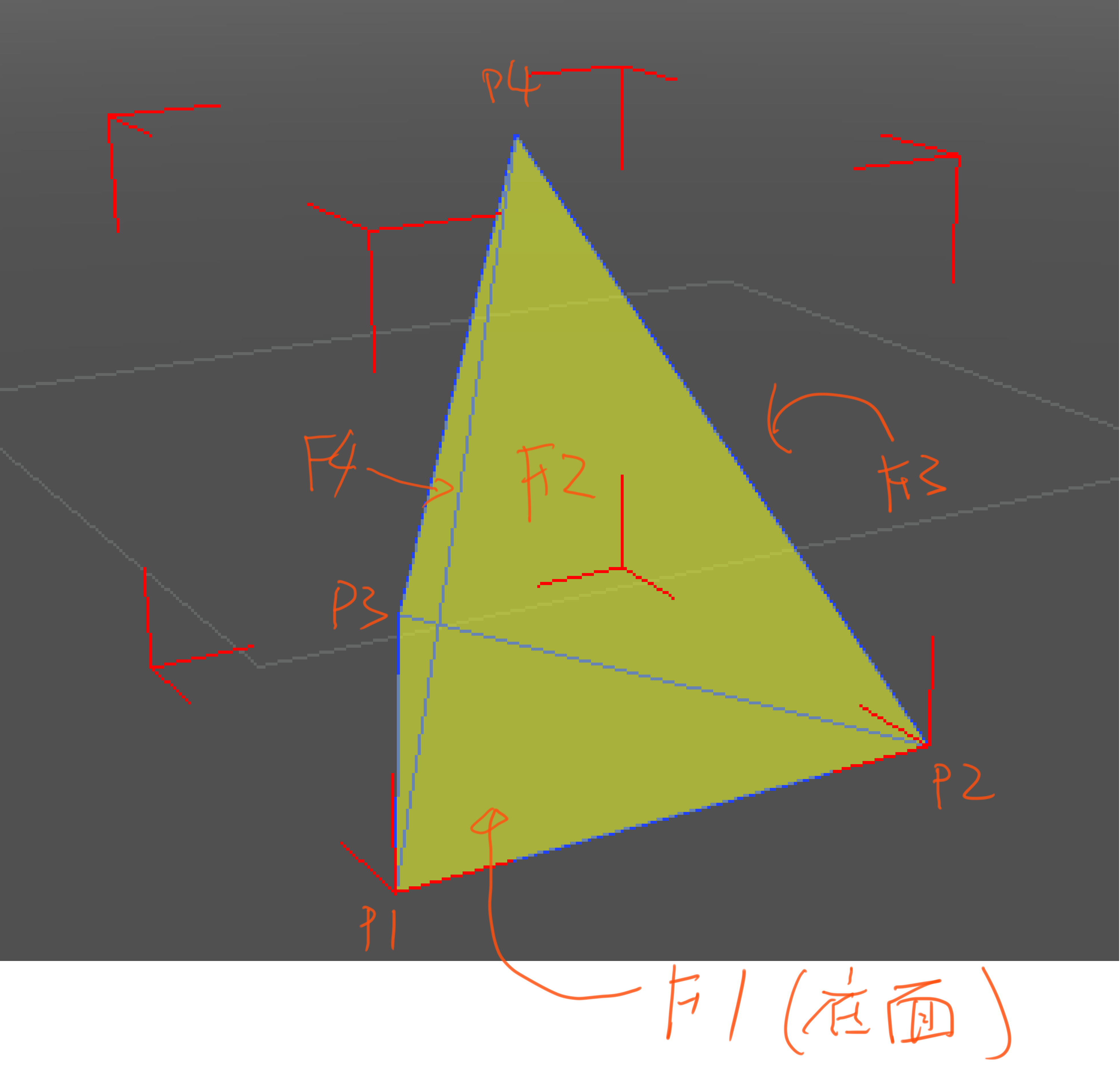
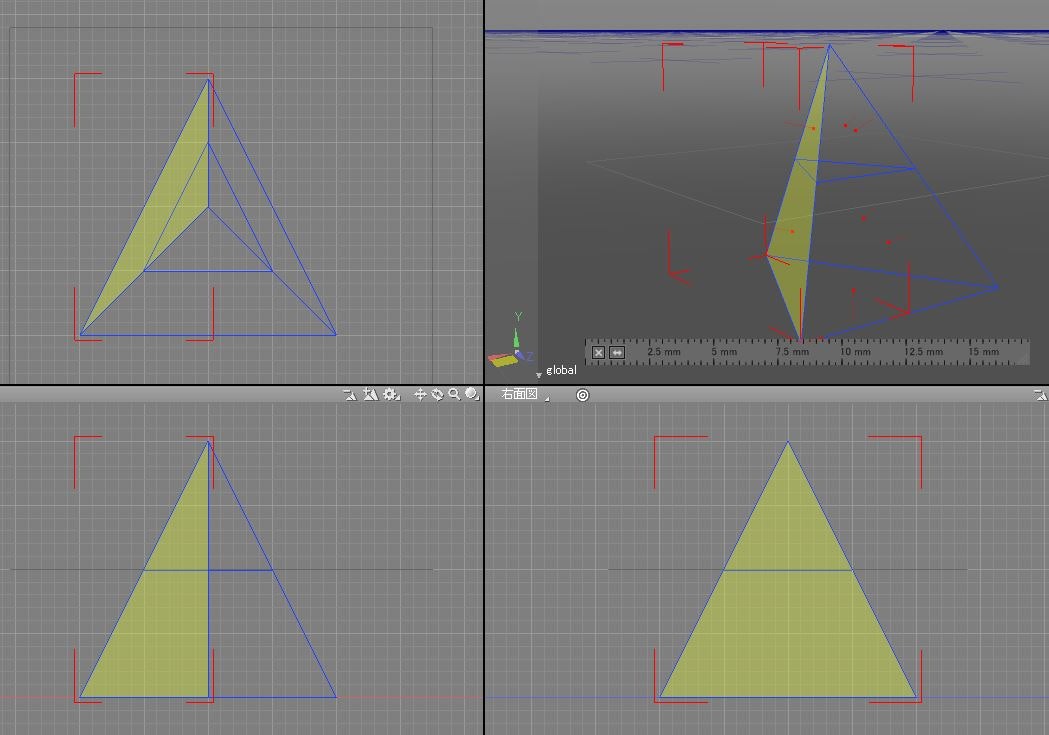
まず、サンプルとして以下の三角錐状のモデルとします。（４面で立体を表現する最小値だと思います）
このモデルの上下方向の真ん中位置で輪切りすることを考えます。
２．１ 材料（モデルデータ）
内部で管理する数値データを以下とします。
- 面情報
| No | 構成頂点1 | 構成頂点2 | 構成頂点3 |
|---|---|---|---|
| 1 | 1 | 3 | 2 |
| 2 | 1 | 2 | 4 |
| 3 | 2 | 3 | 4 |
| 4 | 3 | 1 | 4 |
- 頂点情報
| No | X座標 | Y座標 | Z座標 |
|---|---|---|---|
| 1 | 10 | 10 | 0 |
| 2 | 20 | 10 | 0 |
| 3 | 15 | 20 | 0 |
| 4 | 15 | 15 | 10 |
２．２ アルゴリズム（考え方）
ここで用いる数式を最初に説明します。
y=ax+b
直線の方程式です。aは傾きで
a=(y2-y1)/(x2-x1)
Ｙの増加量÷Xの増加量
bはx=0のときのYの値です。
前記材料と、パラメータとしてのスライス位置(5)を利用します。
- 各面を対象としてループ
- 当該面がスライス位置を跨がる面かチェック
- 面がスライス位置を跨がる場合、スライス対象
上記で、F1のみが対象外となり、F2~F4が対象となります。（F*は面であり面情報のNoを示す）
スライス対象の面に対し以下を行う。
- 面を構成する各稜線に対し以下を行う。
- ＸＺ面投影で２次元化（ＸＺ→ＸＹ）し、Ｙ＝５の位置でのX値を求めます。（生成頂点のX値）
- ＹＺ面投影で２次元化（ＹＺ→ＸＹ）し、Ｙ＝５の位置でのX値を求めます。（生成頂点のY値）
- 生成頂点のZ値をスライス面の5とします。
-
F2の投影イメージ（下左＝ＸＺ投影：下右＝ＹＺ投影）
-
F3の投影イメージ（下左＝ＸＺ投影：下右＝ＹＺ投影）
-
F3の投影イメージ（下左＝ＸＺ投影：下右＝ＹＺ投影）
これにより１つの面から２つの頂点が生成されます。（３つの面を対象とするので、計６つの頂点。ただし、重複を除くと３つの頂点）
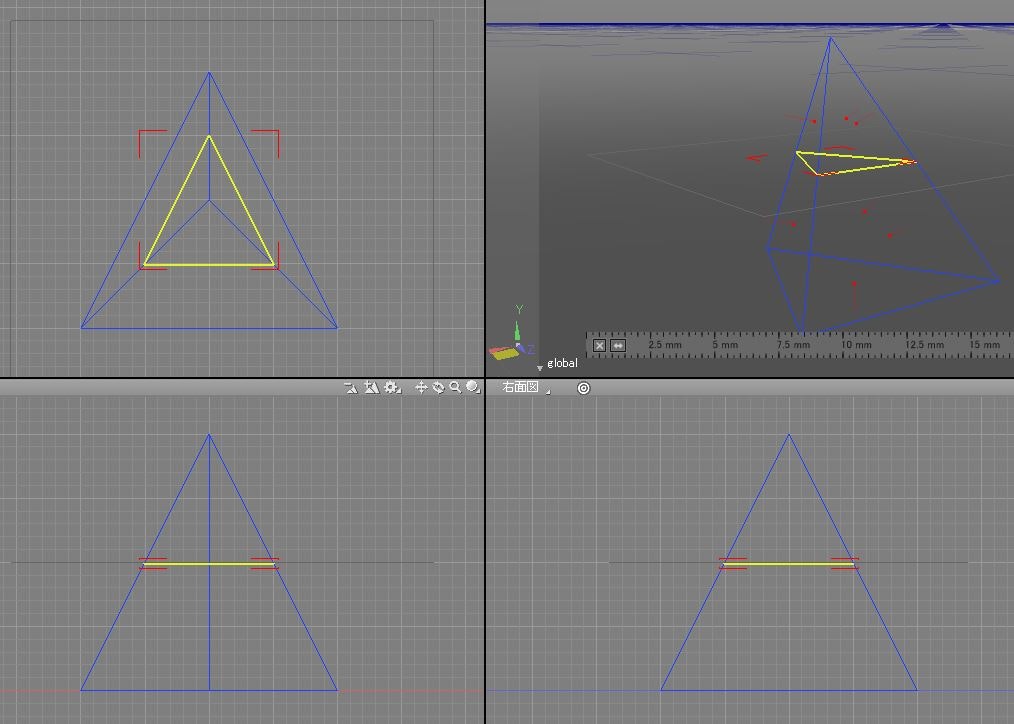
この生成頂点を結んだ閉領域（私のソフト内ではスライスループと呼称）が生成されます。
この後のアルゴリズムはこの閉領域を対象にスライスしていきます。
ＸＺ面で投影したときの値
- F2-L1(P1-P2) → 交点なし
- F2-L2(P2-P4) →(20,0)-(15,10) の直線がY=5のときのX値(y=-2x+40) → X=17.5
- F2-L3(P4-P1) →(15,10)-(10,0) の直線がY=5のときのX値(y=2x-20) → X=12.5
- F3-L1(P2-P3) → 交点なし
- F3-L2(P3-P4) →(15,0)-(15,10) の直線がY=5のときのX値(x=15の垂直線) → X=15
- F3-L3(P4-P2) →(15,10)-(20,0) の直線がY=5のときのX値(y=-2x+40) → X=17.5
- F4-L1(P3-P1) → 交点なし
- F4-L2(P1-P4) →(10,0)-(15,10) の直線がY=5のときのX値(y=2x-20) → X=12.5
- F4-L3(P4-P3) →(15,10)-(15,0) の直線がY=5のときのX値(x=15の垂直線) → X=15
ＹＺ面で投影したときの値
- F2-L1(P1-P2) → 交点なし
- F2-L2(P2-P4) →(10,0)-(15,10) の直線がY=5のときのX値(y=2x-20) → X=12.5
- F2-L3(P4-P1) →(15,10)-(10,0) の直線がY=5のときのX値(y=2x-20) → X=12.5
- F3-L1(P2-P3) → 交点なし
- F3-L2(P3-P4) →(20,0)-(15,10) の直線がY=5のときのX値(x=-2x+40) → X=17.5
- F3-L3(P4-P2) →(15,10)-(10,0) の直線がY=5のときのX値(y=2x-20) → X=12.5
- F4-L1(P3-P1) → 交点なし
- F4-L2(P1-P4) →(10,0)-(15,10) の直線がY=5のときのX値(y=2x-20) → X=12.5
- F4-L3(P4-P3) →(15,10)-(20,0) の直線がY=5のときのX値(x=-2x+40) → X=17.5
各面から求められた点
- F2-NP1 → (17.5, 12.5, 5.0) =F3-NP2
- F2-NP2 → (12.5, 12.5, 5.0) =F4-NP1
- F3-NP1 → (15.0, 17.5, 5.0) =F4-NP2
- F3-NP2 → (17.5, 12.5, 5.0) =F2-NP1
- F4-NP1 → (12.5, 12.5, 5.0) =F2-NP2
- F4-NP2 → (15.0, 17.5, 5.0) =F3-NP1
よって (17.5, 12.5, 5.0)-(12.5, 12.5, 5.0)-(15.0, 17.5, 5.0)-(17.5, 12.5, 5.0)の閉領域が得られる。
３．おわりに
今回は、スライサーソフトのアルゴリズムとして、立体のスライス方法についての紹介でした。
もっと良い（簡単・早い）アルゴリズムや不明点などがあれば教えていただきたいです。
今回のアルゴリズムで得た閉領域を元に、順次G-Code化のための座標を求めていきます。