レイトレーシング(8): 輝度推定による画像生成

(転載その8)

---

• レイトレーシング(1): バージョン1の定義、ベクトル演算
• レイトレーシング(2): Algebraモジュールをいじる
• レイトレーシング(3): フォトンマップ生成の大枠を考える（ついでに光源も）
• レイトレーシング(4): フォトンの生成
• レイトレーシング(5): 物体の定義
• レイトレーシング(6): やっとフォトン追跡
• レイトレーシング(7): 光線追跡処理の大枠
• レイトレーシング(8): 輝度推定による画像生成
• レイトレーシング(9): フィルタ、乱数などで抗ってみる

---

前回、画像生成プログラムの大枠を作成した。今回はフォトンマップから各画素の輝度を計算して画像生成までやってみよう。

各画素の処理

前回の記事でtraceScreenとした処理の実際の中身を考える。フォトンマッピング法は光線追跡法をベースにして、（大雑把に言うと）拡散反射光を求めるのにフォトンマップを使うやりかただ。光源から届く光の量を、光源への光線追跡により求めるかフォトンマップから推定するかの違いだ（と思う）。よって、処理の概略は次のとおり。

1. 視線と物体との交点を求める。
2. 交点における輝度をフォトンマップから推定する。
   1. 交点に近い方からn個のフォトンを抽出する
   2. 推定に不要なフォトンを除く(フォトンの入射方向と交点の法線が反対側とか)
   3. 交点と各フォトンの距離を求める
   4. 一番遠いフォトンの距離を選ぶ(最大半径、面積を求めるのに使う）
   5. 各フォトンによる照度を計算して集計する
   6. 交点の輝度を計算する

1の交点を求めるのは、以前にフォトンマップを作成するときに作ったのでそれをそのまま流用すれば良い。問題は2の輝度の推定だ。

放射輝度推定

1) 交点に近い方からn個のフォトンを抽出する

kdtライブラリはkNearestという関数でn個の近傍点を抽出することができる。まさにこれを使えば良い。抽出には中心点(交点)を他のフォトン情報と同じ型で渡さないといけないので交点からダミーのフォトンを作って渡す。pは交点。

Tracer.hs

ps = kNearest pmap nPhoton $ photonDummy p

photonDummy :: Position3 -> PhotonInfo
photonDummy p = PhotonInfo Red p ex3

2) 推定に不要なフォトンを除く(フォトンの入射方向と交点の法線が反対側とか)

このpsから不要なものを除くが、ここでは交点の平面に対し裏側から入射したフォトンを除外することにしよう。要するに、交点の法線とフォトンの入射方向の内積が負なら省くということだ。nは交点の法線ベクトル。

Tracer.hs

ps' = filter (isValidPhoton n) ps

isValidPhoton :: Direction3 -> PhotonInfo -> Bool
isValidPhoton n pi = n <.> (photonDir pi) > 0

photonDir :: PhotonInfo -> Direction3
photonDir (PhotonInfo _ _ d) = d

ここで、「不要なフォトンを除外したあとでn個のフォトンを使って推定すべきでは？」という指摘があるだろう。その通りだと思うが、ちょっと面倒くさいので今回は無視だ。

3,4) 交点と各フォトンの距離を求める+一番遠いフォトンの距離を選ぶ

これは簡単だ。フォトンから位置を取り出し、交点との差を取って大きさを求めればいい。

Tracer.hs

rs = map (\x -> norm ((photonPos x) - p)) ps'
rmax = maximum rs

haskellだと、リスト処理の関数を使えるので簡単だな。

5,6) 各フォトンによる照度を計算して集計する+交点の輝度を計算する

書籍「フォトンマッピング」には以下の計算式が書いてある。

$
\displaystyle{
L_r = \frac{1}{\pi r^{2}} \sum_{p=1}^N f_r \cdot \Delta \Phi_p
}
$

このうち、このステップで使うのは $f_r \cdot \Delta \Phi_p$ の部分だ。$f_r$ は、今の所は完全拡散反射しか扱わないことにしたのでとても簡単だ。

$
\displaystyle{f_r = \frac{(拡散反射率)}{\pi}}
$

これは、完全拡散反射が微小平面で全ての方向へ均等に反射するため半球全体で積分したもの $\pi$ で割って「輝度」にするためだ。各フォトンから得られた全照度にこれをかければいいので $\sum$ の外に出せる。あとは $\Delta \Phi_p$ の集計だ。各フォトンに一個分のエネルギーを掛けて合計してやればよい。

(shocker-0x15さんご指摘ありがとうございました。修正しました。)

Tracer.hs

rad = foldl (+) radiance0 $ map (photonInfoToRadiance pw) ps'

photonInfoToRadiance :: Double -> PhotonInfo -> Radiance
photonInfoToRadiance pw (PhotonInfo Red   _ _) = Radiance pw 0 0
photonInfoToRadiance pw (PhotonInfo Green _ _) = Radiance 0 pw 0
photonInfoToRadiance pw (PhotonInfo Blue  _ _) = Radiance 0 0 pw

各フォトンは周波数情報しか持たないので、ここでは赤緑青それぞれに一個のエネルギーをかけた「輝度」を返しそれを足し合わせている。radiance0は初期値で「黒」だ。

得られた集計値に $f_r$ を掛け、最後に推定に使った全フォトンが含まれる円の面積で割って完了だ。円の面積は先の求めた最大半径(rmax)を使うのだ。なお $f_r$ を掛けるところは後々の拡張も考え、brdfという関数に切り出す。

Tracer.hs

radiande = (1.0 / (pi * rmax * rmax)) *> (brdf m rad)

brdf :: Material -> Radiance -> Radiance
brdf m rad = (1.0 / pi2) *> ((diffSpec m) <**> rad)

diffSpec :: Material -> Color
diffSpec (Material d) = d

やっとできた。

サンプルシーンの描画

プログラムができたので、早速実行してみよう。以前作った二種類のフォトンマップで画像生成した結果は次のとおり。比較のため、使ったフォトンマップ（を可視化したもの)と古典的光線追跡法で描画したものも並べてみる。

・・・とても微妙な出来栄えだ・・・。今作っているのは「バージョン1」で、点光源だけ、拡散反射のみ、フォトン追跡は反射を無視（相互拡散反射は計算しない）という条件がついているので、ある程度予想していたが、それにしても。。。ちなみに、この条件では古典的光線追跡法は（たぶん）「完璧な画像」になるはずだ。いわゆる環境光成分も入れていないし。だから、理想は一番右の画像にすることだ。

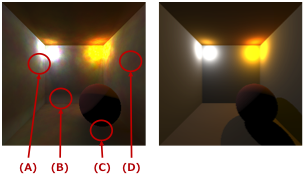
例2の生成画像から、ダメダメな点をいくつかピックアップしてみよう。

• 光源から放射される光にバラツキがあるので綺麗な同心円にならない(A)
• 床面の輝度が光が少ない壁面に滲んでいる(B)
• 球の影がくっきり出ていない、ほとんど影になっていない(C)
• 壁が均一の色になっていない(D)

A)について

有限個のフォトンしか使えないのである程度まばらになるのは仕方がないが、もう少し均一にしたい。そういえば光源から放射されるフォトンは本当に均一なのか疑問だった。また、層化サンプリングも有効かもしれない。現状は球状にばらまいているだけだが、球面をいくつかの部分に分けてその部分ごとにランダムに放射すれば均一性が高まるだろう。次回検証しよう。フォトンの均一性は後述のD)にも影響してくるはずだ。

B)について

交点に近いフォトンを集めて輝度を推定するため致し方ない結果ではある。これを軽減する手法について例の本に記載があるが。。。今はバージョン1のため特に奥の壁にはフォトンが到達しないようになっている。機能拡張をしてフォトン追跡で反射も扱うようにすれば、奥の壁にもフォトンが届き、自ずとこの問題は目立たなくなるだろう。そもそも床面のフォトンを推定に使うことは「問題」ということはなく、それだけのフォトンが近くに到達しているのだから、計算に入れるのは「妥当」と考えるべきだろう。この懸案はバージョン2まで保留する。

C)について

一番ショックなのがこれ。影がほとんどない。フォトンマップはそのアルゴリズム上、フォトンがないと推定できない。このように「まったくフォトンが届かない場所」は正しく描画できなくて当たり前かもしれない。相互拡散反射に対応したら緩和されるかもしれないが、一方、例の本にある「円錐フィルタ」を適用してその効果を見てみようとおもう。これも次回以降だ。

D)について

これはフォトンマッピング法における「誤差」成分なので、フォトン数を増やしたり、輝度推定に使うフォトン数を増やせば低減されるものだ。ただフォトン数を増やすにも限界があるし輝度推定時にフォトンを増やすと推定に使うフォトンの分布範囲が広がってしまうため余計なフォトンを推定に使ってしまい具合が悪い（Cの問題もその一つと言える)。上の画像は推定に200個のフォトンを使ったが、下記に50,100,300も示そう。

個数を増やすとにじみはかなり消えてくる一方、影はなんだかわからなくなっている。逆にn=50にすると影は良くなってきているが壁の滲みはかなりひどい。推定に使うフォトン数の最適値を考えるのは難しいのでとりあえず保留しよう。まずは他の部分の改良だ。

まとめ

今回、曲がりなりにも画像生成までこぎつけ、古典的光線追跡法と比較することができた。思ったほど綺麗な画像にならなかったが、それも改善のしがいがあると捉えよう。次回は光源からのフォトン生成と推定時のフィルタ導入だ。

（今回のソースはこちらから）