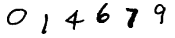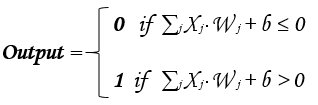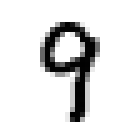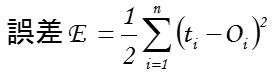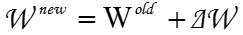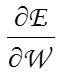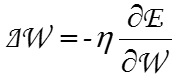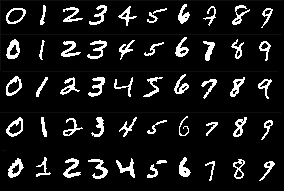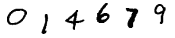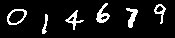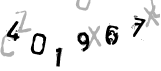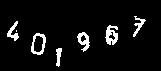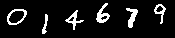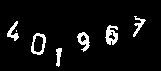これまで、ナイーブベイズ分類器や重回帰分析をWebアプリケーション診断に利用することを試みてきた。
今回はDeep Learningの前哨戦として、ニューラルネットワークの一種である多層パーセプトロンを使ったCAPTCHAの認識(注1)をやってみる。
ただし、ニューラルネットワーク初心者がいろいろ調べながら書いたので、間違った内容が含まれているかもしれない。
その際は、"優しく"ご指摘いただけると幸いだ。
注1:CAPTCHAの認識
今回のターゲットは古典的なCAPTCHAであり、reCAPTCHAのような高度なCAPTCHAは扱わない(現時点では識別が困難なので)。
アジェンダ
0.ニューラルネットワークとは?
1.多層パーセプトロンとは?
2.CAPTCHAとは?
3.Webアプリ診断とCAPTCHA
4.やりかたを考える
5.学習データ
6.入力信号の生成
7.やってみる
8.まとめ
9.参考文献
0.ニューラルネットワークとは?
Wikipediaによると「神経回路網の動きをコンピュータ上で表現することを目指した数学モデル。外部からの入力信号を受けたニューロン(神経細胞)が発火し、シナプスを通じて隣接するニューロンに出力信号(隣接ニューロンから見ると入力信号)が伝播していく様子をシミュレートする。」とのこと。
例えば、私が以下の画像を見たとき、瞬時に「味噌ラーメン」であると認識することができる。
私の脳内では、目から入力された画像(入力信号)が最初のニューロンに伝わり、幾つかのニューロンが発火しながら画像情報を伝播・分類していき、最終的に「これは味噌ラーメンです。」と判断を下している。
※写真は「十味や」の白味噌ラーメン。
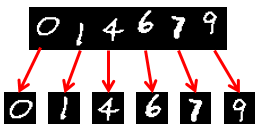
また、以下の画像を見たとき、大抵の人間は「014679」と読むことができる。
人間の脳内では、数十億年の進化の過程で学習された1億数千万のニューロンと数十億のシナプスから構成される視覚野が複雑な画像処理を行うことで、いとも簡単に「味噌ラーメン」や「014679」を認識することができる。
この人間の脳内の処理を単純化して数学的にモデル化したのがニューラルネットワークだ。
ニューラルネットワークを使うことで、複雑な画像認識をコンピュータで行うことができる。
パーセプトロン
ニューラルネットワークでは、パーセプトロンと呼ばれる人口ニューロンを使ってモデルを構築する。
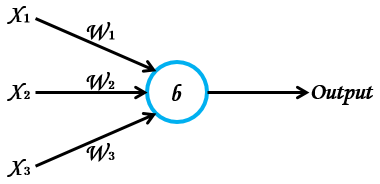
以下の図は、パーセプトロンの簡単な例だ。
青い丸がパーセプトロン。
このニューロンに3つの入力信号(X1、X2、X3)が与えられ、1つの値を出力(Output)する様子を表している。
ちなみに、入力は幾つでも構わない。
※Wは重み、bはバイアスを示す(詳細は後述)。
パーセプトロンの発火
入力信号を伝達するには、パーセプトロンが発火する必要がある。
どうやって発火するのか?
パーセプトロンは必ず発火する訳ではない。
発火(値を出力)するか否かは、パーセプトロン毎に定義された入力の重み付き和とバイアスの加算結果によって決まる。
これを数式で表すと以下の通りとなる。
ざっくり説明すると、各入力の重み付き和とバイアスの加算結果が0以下の場合、出力は「0」(Output無し)、
加算結果が0より大きい場合はパーセプトロンが発火したとみなし、Outputを「1」とする。
すなわち、パーセプトロンの発火を促すには、重み(W)を最適化すれば良い。
ニューラルネットワークでは、重みを最適化することを学習と呼んでいる。
学習
ところで、どうやって学習するのか?
例えば以下の画像をニューラルネットワークに入力(注2)し、数字の「9」であると判断させることを考える。
注2:画像をニューラルネットワークに入力
画像はピクセルで構成されるため、ピクセル毎に情報を入力していく。
例えば、28×28ピクセルの画像ならば、784(=28*28)個の情報が入力信号となる。
例えば、とあるニューラルネットワークは入力画像に対して「8」と認識したとする。
当然ながらこれは間違いだ。
そこで、認識(Output)した値(8)と、予め用意しておいた教師信号(9)との誤差を計算し、その誤差を補正するように重みをUpdateする。
あらゆる入力信号を使って重みをUpdateしていき、誤差が最小になるまで続ける(注3)。
こうして重みの最適化、すなわち学習が行われる。
注3:最小になるまで続ける
学習を行い過ぎると、誤差が最小になるどころか増えていくことがある。
これは過適合、あるいは過学習と呼ばれる。
誤差が増加傾向にあればそれ以降の学習は有害なので、その時点で学習を終了させる。
これは早期終了と呼ばれ、ニューラルネットワークにおける学習テクニックの一つである。
誤差関数
誤差を求めるにも様々なテクニックが存在するが、今回は2乗誤差関数を使用する。
2乗誤差(E)は以下のように定義される。
tは教師信号(正解)、Oはニューラルネットワークの認識(Output)を示している。
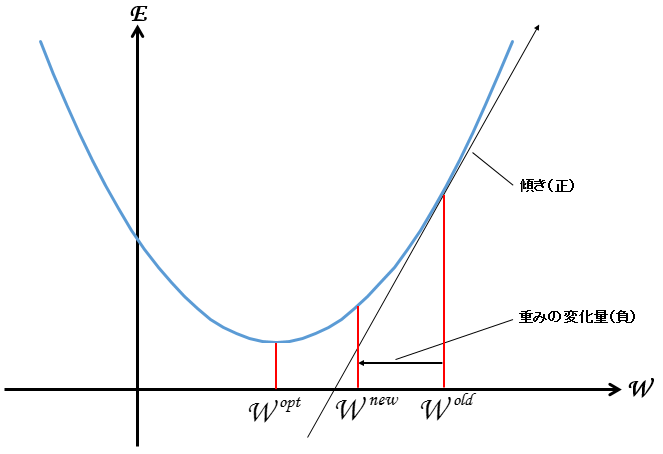
この誤差Eをグラフ化すると以下の通りとなる。
このグラフでは、横軸をとある1つの重み(W)、縦軸を2乗誤差(E)としている。
青い曲線が2乗誤差Eの軌跡だ。
見て分かる通り、曲線の底(傾きが0に近似するとこ)は誤差が(殆ど)無い地点となり、その時の重みはW^opt(最適化された重み)となる。
よって、ニューラルネットワークの学習では、底(W^opt)を目指して重みをUpdateして行けば良いことが分かる。
さて、どうやって重みをUpdateするのか?
非常にシンプルかつ強力な方法がある。
それが勾配降下法だ。
勾配降下法
その名の通り、現在の重みの地点(W^old)から曲線の傾き(勾配)方向に転がり落ちていき、底(誤差が殆ど無い地点)を目指すイメージだ。
学習を繰り返し、W^old からW^optへ近づくように重みをUpdateする。
少し数学的に言うと、W^oldの地点での傾きから変更量⊿Wを求め、新たな重みW^newを求める。
なお、W^oldの地点での傾きは、EをW^oldで偏微分することで求まる。
上図のように、傾きが正の場合はWを減少(変更量が負)させ、負のときはWを増加させる。
よって、変更量⊿Wは学習係数ηを使うと以下のように表すことができる。
ところで、学習係数ηは変化量⊿Wを決める上で極めて大事な値だ。
値が大き過ぎると変化量⊿Wも大きくなり、底を通り過ぎて反対側の斜面に行ってしまう(学習が収束しない)。
逆に小さ過ぎると変化量⊿Wも小さくなり、底への到達に時間がかかる(学習コストが高くなる)。
ちなみに、この学習係数ηはこれといって決まった値はないらしい。
経験則でいい感じの値を求めることが多いようだ。
活性化関数
最後に、パーセプトロンの発火を決定する関数を活性化関数と呼ぶ。
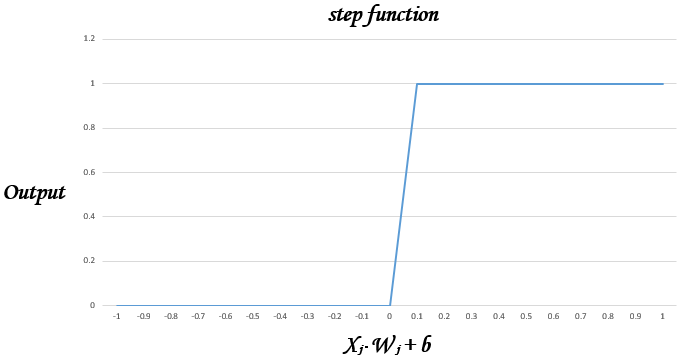
以下の関数はステップ関数と呼ばれ、必ず「0」か「1」を出力する。
実はステップ関数を使うと、学習を行うことが非常に困難であることが分かっている。
例えば上述した画像の予測を「8」としたとする。
予測と正解の差は僅かなため、その僅かな誤差を補正するように重みをUpdateする。
そして、Updateされた重みを使って再度計算を行う。
しかし、ステップ関数は入力の重み付き和とバイアスの和が0を超えると、途端に出力が「1」になる。
逆に、0以下の場合は何も出力されない。
このように、「僅かな誤差」を修正しようと重みを「僅かにUpdate」した場合、出力に変化がないか、全く逆(0から1へ)のように反転してしまう。
当然ながら、出力が反転すればニューラルネットワークの他の箇所の計算結果も連動して変わる。
上述の画像を何とか「9」と判断できたとしても、今度は「9」以外の画像に対するニューラルネットワークの挙動が変わってしまい、その変化をコントロールすることが困難となる。
そこで、重みに「僅かな誤差」を与えたとき、それに対応する「出力も僅かに変化」するような関数が必要になる。
これがシグモイド関数(注4)だ。
注4
今ではシグモイド関数よりソフトマックスと呼ばれる関数を使うことが主流らしい。
今回は大人の事情により、シグモイド関数を使って話を進める。
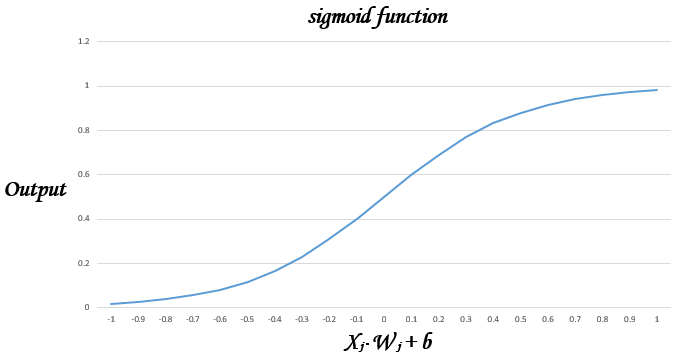
下図はシグモイド関数の振る舞いを表しており、出力は0から1の間の様々な値を取ることが分かる。
シグモイド関数を使用することで、ステップ関数のように極端に出力が変化することを防ぎ、誤差曲線の底に向けて微妙に出力を調整することが可能となる。
つまり、学習が容易になる。
なお、シグモイド関数を活性化関数として実装したニューロンをシグモイドニューロンと呼ぶ(注5)。
注5:シグモイドニューロンと呼ぶ
厳密には、シグモイドニューロンとパーセプトロンは別物なので区別すること。
以上、ニューラルネットワークの基本説明は終了。
今回は誤差関数に2乗誤差、活性化関数にシグモイド関数を使用し、シグモイドニューロンを多層化した多層パーセプトロン(注6)を用いて、CAPTCHAの認識を試みる。
注6:多層パーセプトロン
シグモイドニューロンを使っているのに多層パーセプトロンと呼ぶのは違和感があるが、慣例的にそう呼ぶらしい(理由は誰か教えて)。
1.多層パーセプトロンとは?
Wikipediaによると「層状に並べたシグモイドニューロンが隣接層間でのみ結合した構造を持ち、情報が入力側から出力側に一方向にのみ伝播するニューラルネットワーク」とのこと。
順伝播型(ニューラル)ネットワークとも呼ばれるらしい。
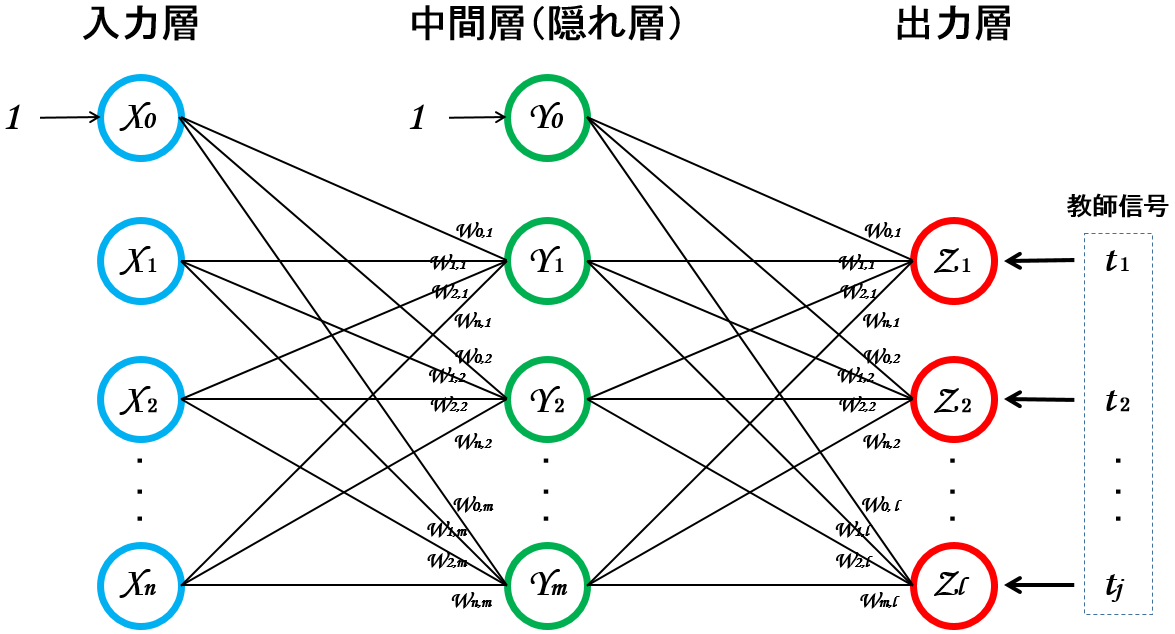
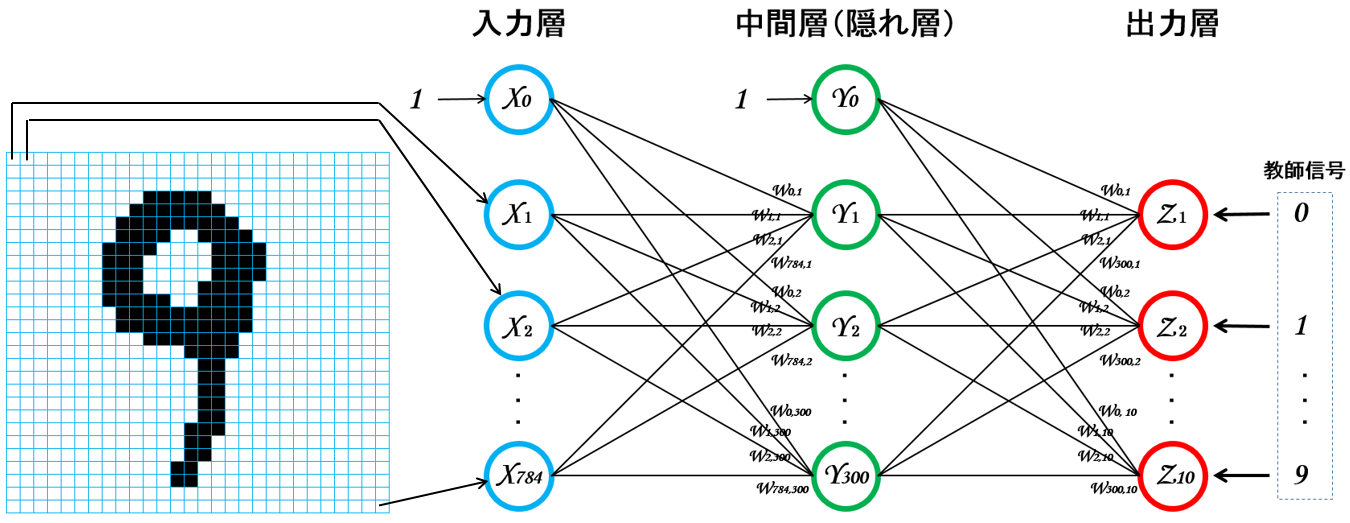
これを図示すると以下のようになる(注7)。
注7
この例は「入力層」、「中間層(1層)」、「出力層」から構成されるシンプルな3層パーセプトロン。
入力層は入力信号の数に応じて調整する(28x28ピクセルの画像を入力信号とする場合、入力層は784個となる)。
中間層は良い計算結果が出るようにいい感じに調整する。
出力層は認識されるオブジェクト数に応じて調整する(例えば、0~9の何れかの数字を認識させたい場合、出力層は10個となる)。
※中間層の重み(W)と出力層の重み(W)は同じもののように描いているが、実際は別々の値になる。
多層パーセプトロンの処理の流れは以下の通り。
- 全ての重み(W)を「-0.1 ≦ W ≦ 0.1」の範囲でランダムに初期化する。
- 学習率を「0 < η ≦ 1」の範囲で設定する。
- 入力信号(X)を入力層に入力する。
- 入力層は入力信号(X)をそのまま出力する。
- 入力信号(X)に重み(W)を乗じて中間層への入力信号を求める。
- 中間層への入力信号をシグモイド関数に通して中間層の出力信号(Y)を出力する。
- 中間層の出力信号(Y)に重み(W)を乗じて出力層への入力信号を求める。
- 出力層への入力信号をシグモイド関数に通して出力層の出力信号(Z)を出力する。
- 出力信号(Z)と教師信号(t)の誤差を算出する。
- 手順9で求めた誤差値を使い、中間層の誤差信号を算出する。
- 手順9、手順10で求めた誤差と誤差信号を使い、重み(W)をUpdateする。
- 全パターンに対する2乗誤差(E)が十分に小さくなったら、学習を終了する。そうでない場合は、全パターンに対して手順3から手順11までの操作を繰り返す。
このように、出力信号(Z)と教師信号(t)の誤差に応じて、出力層から中間層に遡りながら重み(W)をUpdateしていく。
このような学習方法を**誤差逆伝播法(バックプロパゲーション)**と呼ぶ。
なお、学習が完了したら、手順9から手順12までの処理は行わない。
2.CAPTCHAとは?
Wikipediaによると「CAPTCHA(キャプチャ)は チャレンジ/レスポンス型テストの一種で、応答者がコンピュータでないことを確認するために使われる。」とのこと。
よくWebアプリの入力フォームにおいて、人間が入力していることを確かめる目的で「画像に埋め込まれた数字や文字」などの入力を求めるアレだ。
例えば以下のようなもの。
3.Webアプリケーション診断とCAPTCHA
Webアプリ診断をしていると、たまにCAPTCHAを使ったアプリに遭遇することがある。
手持ちのWebアプリスキャナにCAPTCHA解析機能が付いていれば良いが、これが無い場合は悲惨だ。
なぜならば、「スキャナがCAPTCHAを解析できない=スキャナを使って診断できない」ので、全て手作業で診断を行わなければならなくなる(注8)。
当然、コスト超過で赤字プロジェクトになる可能性が高まる。
注8:全て手作業
顧客と調整し、CAPTCHAを無効にして貰うこともある。
この調整が上手くいけば、スキャナで診断することができる。
今回はスキャナへCAPTCHA解析機能を組み込むことを目指し、多層パーセプトロンを使用したCAPTCHAの認識を試みる。
4.やりかたを考える
今回は数字で構成されるCAPTCHAをターゲットにする。
CAPTCHA内の各数字を28x28ピクセルのサイズに切り出し、1字ずつ予測することにする。
よって、入力層は784個、入力信号は784次元のベクトルとなる。
中間層は300とした。
100、200、300、400個と調整した結果、300個が良い感じの精度だったので(こんなんで良いのか?)。
出力層は0~9の何れかを判断するので10個となる。
これで多層パーセプトロンの設計は完了。
次は、この多層パーセプトロンを学習させるためのデータを用意する。
5.学習データ
今回はMNISTの手書き数字データ(注9)を学習データとして使用する。
このデータセットには、28×28ピクセル、70,000個の手書き数字データが含まれている。
なお、各ピクセルは0~255の値を取る。
注9:MNISTの手書き数字データ
MNISTの手書き数字データの簡易版として、scikit-learnのdigit(8×8ピクセル、1,797個)がある。
処理が軽く扱い易いため、多層パーセプトロンの検証に使用される。
上図を見て分かる通り、何となくCAPTCHAに使われる数字に似ているので、学習データとして使えそうだ。
本来はCAPTCHAに使用される数字データを数万単位で収集するのが望ましいが、非常に手間がかかるので、今回はMNISTの手書き数字データを学習データとして使用する。
6.入力信号の生成
ここで入力信号とは、認識させたいCAPTCHA画像の各ピクセル値となる。
なお、今回は以下3種類のCAPTCHAの認識を試みる。
1番目
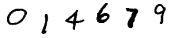
MNISTの手書き数字データを組み合わせた疑似CAPTCHA。
構築した多層パーセプトロンの検証用に使用する。
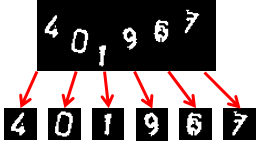
2番目
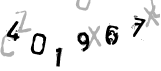
Google画像検索で拾ってきたCAPTCHA。
コンピュータによる解析を防ぐため、背景に灰色のダミー数字が散りばめられている。
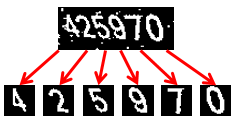
3番目
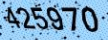
Google画像検索で拾ってきたCAPTCHA。
こちらもコンピュータによる解析を防ぐため、背景色が青色、多数のノイズが入っている。
ところで、学習データと上記CAPTCHAを見比べてみると大きな違いがあることが分かる。
それは、学習データは黒地に白字で数字が描かれているのに対し、CAPTCHAは白地or青地に黒字で数字が描かれている。
入力信号は画像の各ピクセル値となるため、白黒反転の状態では認識が難しい。
そこで、多層パーセプトロンが認識し易いように事前に画像処理を施す。
大津の二値化とネガ・ポジ反転
学習データは白黒(背景:黒、数字:白)の二値画像だ。
よって、CAPTCHAも同じく「背景:黒、数字:白」にする。
多値画像を白黒に二値化するために、大津の二値化アルゴリズムを使う。
さらに、白黒反転させるために、二値化した画像をネガ・ポジ反転させる。
これを行うC#プログラムは以下の通り。
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
using System.Data;
using System.Drawing;
using OpenCvSharp;
using OpenCvSharp.CPlusPlus;
namespace OpenCVTest2
{
class Program
{
static void Main(string[] args)
{
string strInputFileName = @".\Image\input.png";
string strOutputFileName = @".\Image\output.png";
using (IplImage ImgSrc = new IplImage(strInputFileName, LoadMode.GrayScale))
using (IplImage ImgDst = ImgSrc.Clone())
{
// Otsuアルゴリズムで元画像を二値化
Cv.Threshold(ImgSrc, ImgDst, 0, 255, ThresholdType.Otsu);
// 二値化した画像をネガポジ反転
Cv.Not(ImgDst, ImgDst);
// 加工した画像を保存
Cv.SaveImage(strOutputFileName, ImgDst);
}
}
}
}
画像処理にはOpenCvSharpを使用している。
これはOpenCVの.NET版(注10)だ。
注10:OpenCVの.NET版
pythonにもOpenCVのライブラリは存在する。
しかし、2015年6月時点でOpenCVはPython3系に対応していなかったので、C#で行うことにした。
なお、input.pngは画像処理前のCAPTCHA、output.pngは二値化⇒ネガ・ポジ反転後のCAPTCHAとなる。
プログラムでは、読み込んだinput.pngに対し、Thresholdメソッドで二値化している。
第5引数の「ThresholdType.Otsu」は、大津の二値化アルゴリズムを使用することを指定している。
ちなみに、大津のアルゴリズムは、二値化する方法としてはポピュラーとのこと。
そして、二値化した画像に対してNotメソッドを適用してネガ・ポジ反転し、その画像を保存している。
たった10数行のコードでこれらの画像処理を簡単に行うことができる。
非常に便利な世の中になったもんだ。
このコードを通すことで、前述のCAPTCHAは以下のように変換される。
画像処理後のCAPTCHA
1番目
2番目
3番目
画像処理を施すことでノイズが除去されていることに注目してほしい。
2番目のCAPTCHAは、背景にあったダミーの灰色文字が除去されている。
3番目のCAPTCHAは、ドットのノイズがいくらか除去されている。
もっと画像処理を工夫することで、更にノイズを除去できるかもしれない。
数字画像の切り出し
上述したとおり、多層パーセプトロンへの入力信号は、28×28のピクセルデータである必要がある。
また、1回のOutputは「0~9」の何れかの判断になるため、CAPTCHAの各数字を一つずつ入力信号にする必要がある。
すなわち、CAPTCHAから各数字を28×28のサイズで切り出す必要がある。
どうやって1枚の画像から各数字だけを切り出すのか?
これは、領域分割の1手法である「分割・統合法」(注11)を使うと良いらしい。
注11:分割・統合法
参考文献6によると、「領域分割とは、1枚の画像を性質(特徴)が一様である部分領域に分割することです。分割・統合法は、単純で興味深いアルゴリズムを利用しているが特長で、具体的には以下のような目的で利用されます。~(中略)~画像を同じような色の領域に分ける」とのこと。
・・・今回は分割・統合法でCAPTCHAから各数字を切り出す予定だったが、想像以上に実装が難しかったので、今回は3分クッキング方式にした(1枚の画像から各数字が切り出されたと想定して話を進める)。
今回は画像処理がメインテーマではないため良いだろう(言い訳か??)。
これらの各数字画像を多層パーセプトロンに入力することにする。
当然ながら、各数字画像は28×28ピクセルになっている。
7.やってみる
今回は以下二つのpythonコードを作った。
なお、このコードは参考文献7のginrou氏のコードを参考にした。
この記事はニューラルネットの活用例が非常に分かり易く書いてある為、一度読んでみることをお勧めする。
MyMultilayerPerceptron.py
メインコントローラ。
CAPTCHAと学習データ(MNISTの手書き数字データ)を読み込み、多層パーセプトロンの学習と予測を行う。
# !/usr/bin/env python
from mlp import *
import os
import numpy
import gzip, pickle
import pylab
# 訓練データの読み込み
def train_data_read(file_path):
# 訓練用データ(MNIST)のロード
f = gzip.open(file_path, 'rb')
train, valid, test = pickle.load(f, encoding='latin1')
f.close()
return (train[0], train[1], train[0].shape[0])
# 1-of-K表記への変換
def to_formatted_array(number):
ret = numpy.zeros(10)
ret[number] = 1
return ret
if __name__ == "__main__":
# 識別対象のCAPTCHA画像が格納されているファイルパスを定義
captcha_path = 'C:\MNIST\captcha\captcha0'
# 訓練済みデータを格納するpklファイルパスを定義
trained_mlp_path = os.path.join('.\\', 'trained_mlp.npz')
# 訓練用データ(MNIST)のファイルパスを定義
train_data_path = os.path.join('C:\\MNIST', 'mnist.pkl.gz')
# 正解ラベルの定義(結果表示用)
answerLabel = [0, 1, 4, 6, 7, 9]
# CAPTCHA画像データを64次元のベクトルに変換
# RGB毎の配列からR要素のみを抽出(次元削減)
img_captcha = []
analize_data = []
captcha_files = os.listdir(captcha_path)
for file in captcha_files:
img_captcha = pylab.imread(os.path.join(captcha_path,file))
#img_captcha_r = img_captcha[:, :, 0]
img_captcha_r = img_captcha[:, :]
img_captcha_Array = numpy.asarray(img_captcha_r)
d_captcha = img_captcha_Array.shape[0] * img_captcha_Array.shape[1]
img_captcha_wide = img_captcha_Array.reshape(1, d_captcha)
analize_data.append(img_captcha_wide)
# 訓練済みデータ(pkl)が存在する場合、既存の訓練済みデータを使用
if os.path.exists(trained_mlp_path):
nn = NeuralNetwork(in_size = 784, hidden_size = 300, out_size = 10)
nn.load(trained_mlp_path)
# 訓練済みデータが存在しない場合、新たに訓練を実施
else:
# ニューラルネットワークの構築
# 入力層=784(28*28)、中間層=300、出力層=10(0~9)
nn = NeuralNetwork(in_size = 784, hidden_size = 300, out_size = 10)
# 訓練データの読み込み(画像本体、画像の正解ラベル、訓練データの長さ)
images, labels, length = train_data_read(train_data_path)
# 多層パーセプトロンの学習
for i in range(length):
# 訓練データを1個ずつ読み込む
x = images[i]
# 教師信号の数字を1-of-K表記に変換
y = to_formatted_array(labels[i])
# 学習
nn.fit(x, y)
# 学習結果をファイルに保存(学習コストが高いため)
# 次回からは学習を行わずに、本ファイルを読み込んで使用する
nn.save(trained_mlp_path)
ok = 0
for i in range(len(analize_data)):
# 認識対象データを1個ずつ読み込む
x = analize_data[i]
# 認識対象の正解データを1個ずつ読み込む
y = answerLabel[i]
# 学習させた多層パーセプトロンで認識対象データの予測を行う
answer = int(nn.predicate(x[0]))
# 予測値と正解データを標準出力する
print("No.{0:d} : predict => {1:d} , answer = > {2:d}".format(i, answer, int(y)))
# 予測値と正解データが一致している場合、ok(正解)を1インクリメントする
if int(y) == answer:
ok += 1
# ok(正解)の数と認識対象データ数を基に正解率を標準出力する
print("{0:05d} / {1:05d} = {2:3.2f}%".format(ok, len(analize_data), 100*ok/len(analize_data)))
mlp.py
多層パーセプトロンの処理。
上述したシグモイド関数や2乗誤差の処理、誤差逆伝播法の処理などを行っている。
# !/usr/bin/env python
from math import exp
import numpy
# シグモイド関数
def sigmoid_func(x):
return 1.0 / (1.0 + exp(-x))
def sigmoid(array):
return numpy.vectorize(sigmoid_func)(array)
# 多層パーセプトロンを表現するクラス
class NeuralNetwork:
# 重み(W)をランダムな値に初期化する
def __init__(self, in_size, hidden_size, out_size):
# 中間層の重みを初期化
self.hidden_weight = 0.1 * (numpy.random.random_sample((hidden_size, in_size+1)) - 0.5)
# 出力層の重みを初期化
self.output_weight = 0.1 * (numpy.random.random_sample((out_size, hidden_size+1)) - 0.5)
# 学習データ(x)、教師信号(t)、学習係数=0.1で学習する
def fit(self, x, t, update_ratio = 0.1):
# 中間層・出力層のシグモイドニューロンからのOutputを求める
z, y = self.fire(x)
# バックプロパゲーションの処理
dy = ( y - t ) *y * ( 1 - y )
dz = (self.output_weight.T.dot(dy))[1:] * z * ( 1- z )
output_input = numpy.r_[ numpy.array([1]), z ]
self.output_weight -= update_ratio * dy.reshape(-1,1) * output_input
hidden_input = numpy.r_[ numpy.array([1]), x ]
self.hidden_weight -= update_ratio * dz.reshape(-1,1) * hidden_input
# シグモイドニューロンの発火(中間層、出力層のOutput値を計算)
def fire(self, x):
z = sigmoid(self.hidden_weight.dot(numpy.r_[ numpy.array([1]), x ]))
y = sigmoid(self.output_weight.dot(numpy.r_[ numpy.array([1]), z ]))
return (z, y)
# 認識させたい入力信号(x)を受け取り、
def predicate(self, x):
z, y = self.fire(x)
return numpy.array(y).argmax()
# 学習結果をファイルに保存する
def save(self, filepath):
numpy.savez(filepath, hidden = self.hidden_weight, output = self.output_weight)
# 学習済みデータのロード
def load(self, filepath):
npzfiles = numpy.load(filepath)
self.hidden_weight = npzfiles['hidden']
self.output_weight = npzfiles['output']
これを使ってCAPTCHAの認識を行ってみる。
私の環境(Intel Corei5 1.8GHz、Mem:8.00GB、SSD、GPU非搭載)だと、学習に3分ほどかかる。
が、予測はほんの一瞬だ。
No.0 : predict => 0 , answer = > 0
No.1 : predict => 1 , answer = > 1
No.2 : predict => 4 , answer = > 4
No.3 : predict => 6 , answer = > 6
No.4 : predict => 7 , answer = > 7
No.5 : predict => 9 , answer = > 9
00006 / 00006 = 100.00%
多層パーセプトロンの予測が「predict」、予め用意した正解が「answer」だ。
見事に100%の認識率だ。
といっても、本CAPTCHAは学習データを基に生成したので当たり前かもしれない。
No.0 : predict => 0 , answer = > 0
No.1 : predict => 1 , answer = > 1
No.2 : predict => 6 , answer = > 4
No.3 : predict => 8 , answer = > 6
No.4 : predict => 8 , answer = > 7
No.5 : predict => 3 , answer = > 9
00002 / 00006 = 33.33%
※各数字画像を昇順に予測している。
とたんに認識率が下がった!!
6->8、9->3は人間でも間違える可能性はあるが、7->8は流石にないだろう。。
No.0 : predict => 0 , answer = > 0
No.1 : predict => 2 , answer = > 2
No.2 : predict => 6 , answer = > 4
No.3 : predict => 5 , answer = > 5
No.4 : predict => 3 , answer = > 7
No.5 : predict => 8 , answer = > 9
00003 / 00006 = 50.00%
※各数字画像を昇順に予測している。
ちょっと安心。
認識率は50%だ。
0や1、2や5といった特徴的な数字は認識率が高いが、8や9、4といった複雑な数字はこの多層パーセプトロンでは認識することが難しいようだ。
このままじゃ実用に耐えられないので、種々の改善が必要だろう。
8.まとめ
初めてニューラルネットワークというものを実装し、数字画像の認識をやってみた。
認識率はまぁまぁだったが、改善の余地はあると思われる。
今回は数字の認識を行ったが、ニューラルネットワークを拡張した畳み込みネットを使うと、画像認識(Googleの猫認識など)も出来るらしい。
また、再帰的ニューラルネットを使えば、文章の予測も行えるらしい(This is aの後に、penが来ることを予測する、など)。
更に、遺伝的アルゴリズムというものを使うと、AIがマリオをクリアすることもできるようだ。
ニューラルネットワークの可能性は大きいので、今後いろいろ試していきたい。
また、今回はシグモイド関数や2乗誤差関数を使用したが、他にも有用な関数(ソフトマックス関数、交差エントロピーなど)が存在するらしい。
今後はこれらを組み合わせ、より認識率を上げていき、スキャナに実装したいと思う。
更に、上述で言い訳した分割・統合法を実装し、「CAPTCHAの取得」->「数字の切り出し」->「その数字を認識」まで一貫したコードを作りたいと思う。
これをスキャナに実装すれば、古典的なCAPTCHAは難なく乗り越えられるかもしれない。
※古典的なCAPTCHAを使ってるWebアプリがあれば、のお話だが。
9.参考文献
- 深層学習
- 誤差逆伝播法について
- ニューラルネットワークと深層学習
- ニューラルネットワーク入門
- OpenCvSharpをつかう
- 画像を同じ特徴を持つ複数の領域に分ける方法
- ニューラルネットワークで数字を認識するWebアプリを作る
以上