前回はナイーブベイズ分類器を使って、重点診断対象の画面を分類した。
今回は重回帰分析を使って、診断工数を見積もってみる。
アジェンダ
0.重回帰分析とは?
1.診断工数の見積とは?
2.やりかたを考える
3.やってみる
4.まとめ
5.参考文献
0.重回帰分析とは?
重回帰分析の前に、そもそも回帰分析って何?
Wikipediaによると、「回帰分析(かいきぶんせき、英: regression analysis)は、従属変数(目的変数)と連続尺度の独立変数(説明変数)の間に式を当てはめ、従属変数が独立変数によってどれくらい説明できるのかを定量的に分析することである。」とのこと。
私のような統計学の素人にはよく分からない説明だ。
いろいろ調べたところ、過去の実績データ(統計データ)を分析して未来を予測するものらしい。
手法も種々存在しており、代表的なものとして単回帰分析や重回帰分析などが存在するとのこと。
単回帰分析
とある1つの目的変数を1つの説明変数を使って予測するもので、その2つのパラメータの関係性を一次方程式の形で表わすことができる。
単回帰分析の説明でお馴染みの「身長と体重」の関係を例にしてみる。
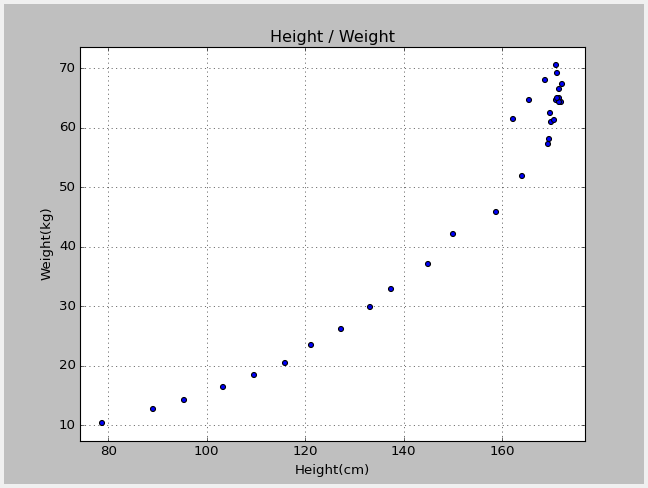
以下のグラフは、総務省統計局のHPに掲載されている「平成24年度の身長と体重の平均値」データをプロットしたものだ。
X軸が身長(cm)、Y軸が体重(kg)を表している。
このデータを単回帰分析し、体重(目的変数)と身長(説明変数)の関係を一次方程式で表すと以下となる。
Y(体重) = X(身長)*0.6847 - 54.4681
例えば身長(X)が120cmの場合、体重(Y)は約28kgと予想できる。
また、身長が160cmの場合、体重は約55kgと予想できる。
このように、データの集合を分析し、説明変数(X)が1つの一次方程式を導くのが単回帰分析だ。
なお、単回帰分析はPython用の統計処理モジュール「statsmodels」を使うことで、非常に簡単に実行することができる。
以下、コード例。
# -*- coding: utf-8 -*-
import statsmodels.api as sm
import pandas as pd
def main():
# 分析対象データの読み込み
data = pd.read_csv('sample.csv', skiprows=1, names=['height', 'weight'], encoding='UTF_8')
# 身長を説明変数として定義
x = data[['height']]
# 定数項をxに加える
x = sm.add_constant(x)
# 体重を目的変数として定義
y = data[['weight']]
# モデルを定義
model = sm.OLS(y, x, prepend=False)
# 単回帰分析の実行
results = model.fit()
# 分析結果の表示
print(results.summary())
if __name__ == '__main__':
main()
OLS Regression Results
==============================================================================
Dep. Variable: weight R-squared: 0.934
Model: OLS Adj. R-squared: 0.932
Method: Least Squares F-statistic: 412.8
Date: Mon, 11 May 2015 Prob (F-statistic): 1.07e-18
Time: 23:50:15 Log-Likelihood: -95.217
No. Observations: 31 AIC: 194.4
Df Residuals: 29 BIC: 197.3
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [95.0% Conf. Int.]
------------------------------------------------------------------------------
const -54.4681 5.112 -10.656 0.000 -64.923 -44.014
height 0.6847 0.034 20.318 0.000 0.616 0.754
==============================================================================
Omnibus: 3.134 Durbin-Watson: 0.125
Prob(Omnibus): 0.209 Jarque-Bera (JB): 1.446
Skew: 0.090 Prob(JB): 0.485
Kurtosis: 1.957 Cond. No. 800.
==============================================================================
Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
実行結果の見方はこうだ。
- 決定係数(R-squared: 0.934)
- F検定(F-stat: 412.8、 p-value: 1.07e-18)
- t検定(係数 height:t-stat=20.318、p-value=0.000、定数 const:t-stat=-10.656、p-value=0.000)
決定係数は**93%**のため、一次方程式はデータ構造をよく表していることを意味する。
F値(F-stat)が大きく、有意確率(p-value)が十分に小さいため、モデルが妥当であると判断できるらしい。
最後に係数height、定数constの有意確率双方が十分に小さい値のため、係数、定数とも妥当であると判断できるらしい。
正直F検定とt検定の意味がよく分からないが、そういうことらしい。。
なお、constの「-54.4681」が一次方程式の切片、heightの「0.6847」が傾きを表している。
重回帰分析
とある1つの目的変数を複数の説明変数を使って予測するもの。
先程の例では、体重(目的変数)を予測するために身長(説明変数)のみ使用したが、腹囲(説明変数)や胸囲(説明変数)を使用すると、予測精度を高めることができるかもしれない。
このように、複数の説明変数を使って目的変数を求めるのが重回帰分析だ。
今回は、重回帰分析を使ってWebアプリ診断の工数を見積もってみる。
1.診断工数の見積とは?
診断工数とは、その名の通りWebアプリケーション診断を行うための工数だ。
診断を実行し、診断結果を分析し、顧客にレポートするまでの一連の工数だ。
以前の投稿で記載したとおり、診断対象の単位は画面となる(少なくとも私の場合)。
よって、対象の画面が増えれば診断工数も増えることが多い。
しかし、診断工数は画面数以外の要因でも変動する。
よって、精度の高い診断工数を見積もるには、画面数以外の要因を正確に把握することが重要となる。
そのためには数多くの診断経験が必要であり、個人的には3年以上の診断経験が必須だと考えている。
今回は、この診断工数の見積を重回帰分析を使って実現してみようと思う。
2.やりかたを考える
重回帰分析を行う上で重要なのは以下2点だ。
- 目的変数(Y)の定義
- 説明変数(X)の定義
それぞれどうやって定義するのか?
目的変数
今回導き出したいのは「診断工数」だ。
よって、目的変数は診断工数となる。
説明変数
診断工数に影響を与える要因が説明変数になる。
私が直ぐに思いつく要因は以下の通りだ。
- 診断対象の画面数
- パラメータ数
- Webサーバのレスポンス速度
- 診断対象アプリの複雑度
- 検出される脆弱性数
- 診断員の経験値
など。
上記すべてを説明変数に使用できれば良いが、「図解でわかる重回帰分析【後編】〜陥りがちな10の失敗パターン〜」にもある通り、説明変数が多すぎると期待通りの結果を得られないこともあるようだ。
よって今回は、(説明のし易さもあるが)以下の3つを説明変数として使用する。
- 診断対象の画面数
- Webサーバのレスポンス速度
- 診断員の経験値
これで目的変数と説明変数の定義が完了した。
それでは、さっそく重回帰分析を実行してみよう。
3.やってみる
先ずは分析対象のデータを用意する。
当該データは予測精度を決定付けるため、非常に重要だ。
理想は、過去の案件データ(実績値)を用いた方が良いが、今回は疑似案件データを使うことにする。
データには77案件分の情報が含まれており、各列の説明は以下の通り。
- 1列目:man_hour:診断工数の実績値(単位は時間(h))
- 2列目:target_num:診断対象の画面数
- 3列目:exp:診断員の経験値(0.8:熟練者、0.9:中級者、1.0:初級者)
- 4列目:speed:レスポンス速度(1.0:速い、1.1:普通、1.2:遅い)
ところで、3列目と4列目を定量的に表すことは難しい。
今回はざっくりと定義したが、定性的な情報を上手く定量化することが、データサイエンティストと呼ばれる人々の腕の見せ所なのだろうか。
重回帰分析を行うコードは以下の通り。
# -*- coding: utf-8 -*-
import statsmodels.api as sm
import pandas as pd
from matplotlib import pyplot as plt
def main():
# 過去の案件データの取り込み(診断工数、画面数、診断員の経験値、Webサーバのレスポンス速度)
data = pd.read_csv('pen_manhour_single.csv', skiprows=1, names=['man_hour', 'target_num', 'exp', 'speed'], encoding='UTF_8')
# 画面数、診断員の経験値、Webサーバのレスポンス速度を説明変数として定義
x = data[['target_num', 'exp', 'speed']]
# 定数項をxに加える
x = sm.add_constant(x)
# 診断工数を目的変数yとして定義
y = data['man_hour']
# モデルを定義
model = sm.OLS(y, x, prepend=False)
# 重回帰分析の実行
results = model.fit()
# 分析結果の表示
print(results.summary())
if __name__ == '__main__':
main()
OLS Regression Results
==============================================================================
Dep. Variable: man_hour R-squared: 0.990
Model: OLS Adj. R-squared: 0.990
Method: Least Squares F-statistic: 2398.
Date: Thu, 14 May 2015 Prob (F-statistic): 8.09e-73
Time: 00:19:30 Log-Likelihood: -278.33
No. Observations: 77 AIC: 564.7
Df Residuals: 73 BIC: 574.0
Df Model: 3
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [95.0% Conf. Int.]
------------------------------------------------------------------------------
const -340.8740 21.556 -15.814 0.000 -383.834 -297.914
target_num 1.4761 0.018 83.984 0.000 1.441 1.511
exp 193.7823 14.175 13.671 0.000 165.532 222.032
speed 149.5108 16.739 8.932 0.000 116.150 182.872
==============================================================================
Omnibus: 1.681 Durbin-Watson: 1.905
Prob(Omnibus): 0.431 Jarque-Bera (JB): 1.692
Skew: -0.334 Prob(JB): 0.429
Kurtosis: 2.714 Cond. No. 3.37e+03
==============================================================================
Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
実行結果から、目的変数(man_hour)と説明変数(target_num、exp、speed)の関係を一次方程式で表すと以下となる。
man_hour = target_num1.4761 + exp193.7823 + speed*149.5108 - 340.8740
この方程式を使うと、まずまずの結果が得られる。
精度が非常に高いとは言えないが、それなりの結果といったところだろう。
4.まとめ
重回帰分析を使って、診断工数の見積もりを行った。
その結果、まずまずの精度で診断工数を予測することができた。
さらに予測精度を上げるには、以下2点が重要だろう。
- 分析対象データの質を上げる(過去の案件データの実績値を使う)
- 1のデータを解析し、使用する説明変数を厳密に定義する
最後に、重回帰分析で得られる結果は、あくまでも統計データを元にした予測値だ。
また、データに表れない要因が存在する可能性は否定できない。
そのため、分析結果は参考情報とし、人の判断と併せて活用する方が良いかもしれない。
5.参考文献
以上