こちらの記事の続きです。
オセロ〜「実装 ディープラーニング」の三目並べより(1)
http://qiita.com/Kumapapa2012/items/cb89d73782ddda618c99
オセロ〜「実装 ディープラーニング」の三目並べより(2)
http://qiita.com/Kumapapa2012/items/f6c654d7c789a074c69b
後続の記事はこちら。
オセロ~「実装 ディープラーニング」の三目並べより(4)[終]
http://qiita.com/Kumapapa2012/items/9cec4e6d2c935d11f108
最初の記事で、活性化関数について触れましたが、dying ReLU の可能性があるということで、これを回避する方法の中で、おそらく最も簡単かつ高速な Leaky ReLU を使って、オセロゲームをさせててみました。
コードはこちらにあります。
https://github.com/Kumapapa2012/Learning-Machine-Learning/tree/master/Reversi
Leaky ReLU
ReLU は、0 未満の値はすべて 0 とする活性化関数です。
f = \max(0,x)
今回の NN は全結合ですが、以前記述したとおり、dying ReLU という問題が発生しえます。
これを解決するものの一つが、Leaky ReLU で、負値に小さな傾きをつけます(chainer の場合デフォルト 0.2)。
{f = \begin{cases}
x & (x>0)
\\
0.2x & (x<=0)
\end{cases}
}
これにより、傾き 0 の箇所がなくなります。
これは個人的な解釈ですが、dying ReLU は、要するに負値の傾きが 0 であるのが原因なのだから、傾きをつけてればよい。しかし ReLU の「正の傾きが 1 、負の傾きが 0 である」ことによる、微分が簡単、計算と学習(逆伝搬)が早い、といった特徴はなるべく残したいので、傾きは小さく、ということが、Leaky ReLU の特徴と考えています。
Leaky ReLU を使ってみた。
agent.py のコードを8行だけ変えて、ReLU から Leaky ReLU に活性化関数を変更。
$ diff ~/git/Learning-Machine-Learning/Reversi/agent.py agent.py
47,55c47,55
< h = F.relu(self.l1(x))
< h = F.relu(self.l20(h))
< h = F.relu(self.l21(h))
< h = F.relu(self.l22(h))
< h = F.relu(self.l23(h))
< h = F.relu(self.l24(h))
< h = F.relu(self.l25(h))
< h = F.relu(self.l26(h))
< h = F.relu(self.l27(h))
---
> h = F.leaky_relu(self.l1(x)) #slope=0.2(default)
> h = F.leaky_relu(self.l20(h))
> h = F.leaky_relu(self.l21(h))
> h = F.leaky_relu(self.l22(h))
> h = F.leaky_relu(self.l23(h))
> h = F.leaky_relu(self.l24(h))
> h = F.leaky_relu(self.l25(h))
> h = F.leaky_relu(self.l26(h))
> h = F.leaky_relu(self.l27(h))
その結果、6x6 盤では安定して勝率が上がるようになりました。
Leaky ReLU 使用時(slope=0.2)
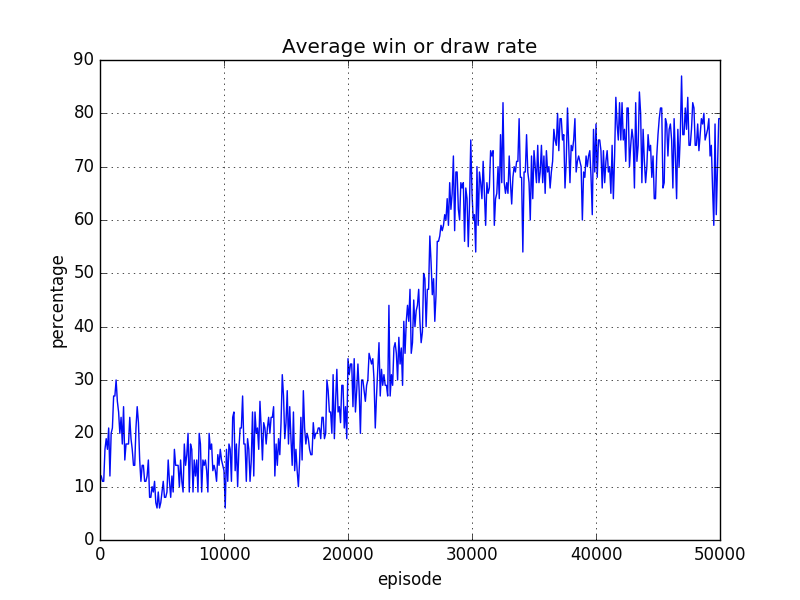
前回の結果とはかなり異なります。やはり、dying ReLU が発生していたのかな?
ReLU 使用時
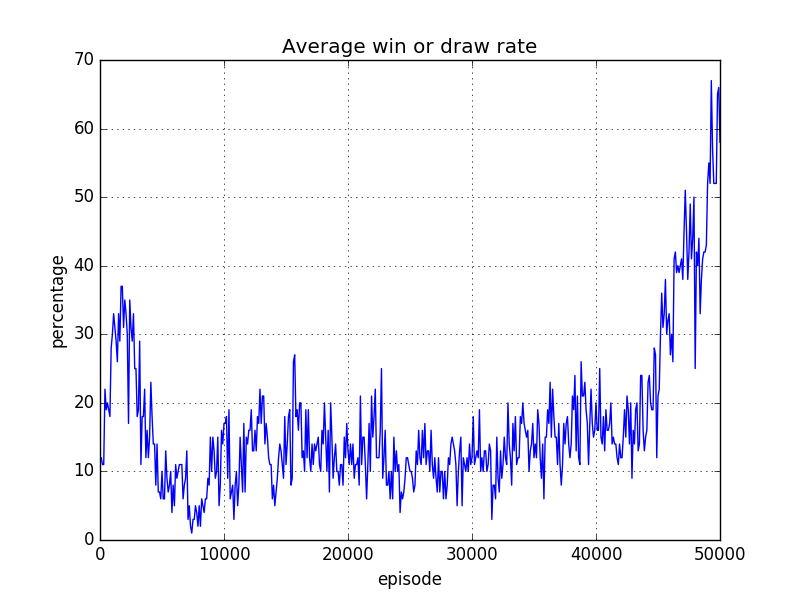
続いて 8x8盤の場合・・・勝率が安定しませんでした/(^o^)\
Leaky ReLU 使用時(slope=0.2)
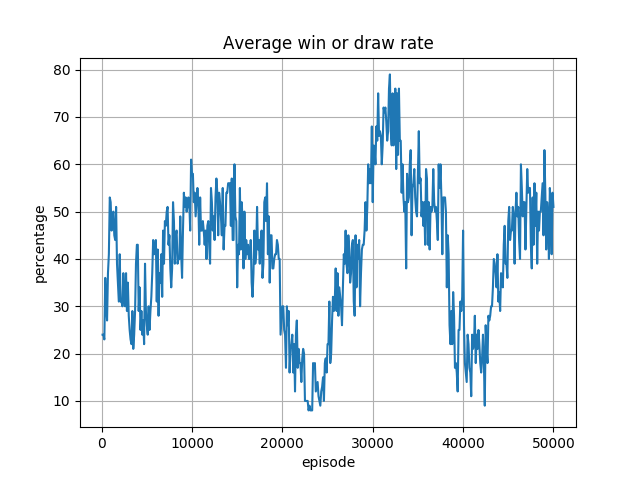
最初の結果では、最終的に勝率は収束しつつあるように見えます。
ReLU 使用時
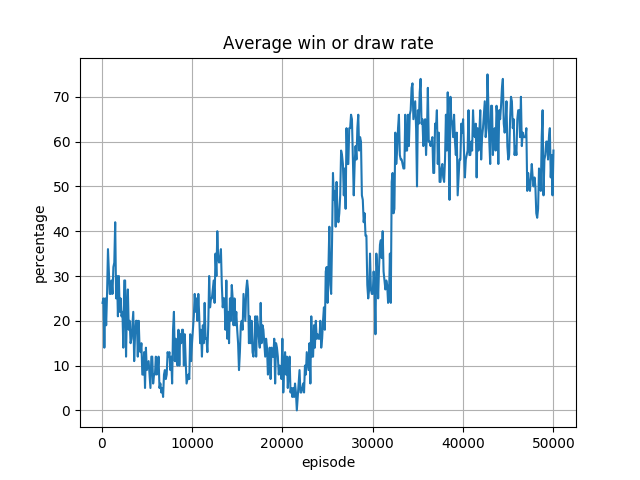
非常に単純に考えると、勝率が ReLU つまり Slope=0 の Leaky ReLU のとき、収束しそうになり、Slope=0.2 の Leaky ReLU のときに収束しないのなら、その間の値に最適な値があるのかもしれません。後で Slope=0.1 でも試してみたいと思います。
しかしより大きな問題は、勝率に波がある状況です。
波打っているということは、学習がほどよいところで止まらないということと思われます。これには学習率が関連しているようです。書籍「ゼロから作るディープラーニング」6章をによると、学習率は要するに、重み W の更新の度合いを示す係数で、高いほど、W の更新の度合いが大きく、早く学習が進みますが、発散する可能性がある1。しかし、小さすぎると、学習が遅くなりすぎてしまう。というものです。
今回使用している RMSPropGraves の引数 lr (Learning Rate=学習率)は 0.00025 です。chainer の RMSPropGraves ではデフォルトの lr が 0.0001 なので、本サンプルのものは少し大きめです。
おそらくこの 0.00025 はサンプルの三目並べの学習速度に最適化した値であり、今回のオセロの 8x8 盤の場合には大きすぎて、W の値が安定せず、結果上記グラフのように勝率が安定しなくなったのだと考えられます。
このため、学習率を低く設定してどうなるかについても、今後試してみたいと思います。2
参考文献
コンピューターオセロ
https://ja.m.wikipedia.org/wiki/%E3%82%B3%E3%83%B3%E3%83%94%E3%83%A5%E3%83%BC%E3%82%BF%E3%82%AA%E3%82%BB%E3%83%AD
Neural Networkでの失敗経験やアンチパターンを語る
http://nonbiri-tereka.hatenablog.com/entry/2016/03/10/073633
(ほかは後日追加)