【数Ⅲ】文系卒社会人が統計・機械学習を理解するために勉強した

#サマリ
統計・機械学習を理解するために数学の知識が足らず勉強を始めました。その経緯などは「文系卒が統計・機械学習を理解するための数学勉強方法」を参照ください。
参考リンク

• 数Ⅰ:「【数Ⅰ】文系卒社会人が統計・機械学習を理解するために勉強した」
• 数A:「【数A】文系卒社会人が統計・機械学習を理解するために勉強した」
• 数Ⅱ: 「【数Ⅱ】文系卒社会人が統計・機械学習を理解するために勉強した」
• 数B: 「【数B】文系卒社会人が統計・機械学習を理解するために勉強した」
  ※2003年以前の学習指導要領に準拠しています。

項目	内容
総勉強時間	26h(約1.5か月)
使用教材	長岡先生の授業が聞ける高校数学の教科書数学 (考える大人の学び直しシリーズ) 数Ⅲは約200ページの内容です。
勉強開始前の状態	数学の勉強は高校以来やっていない状態。数学は嫌いではないが、高校2年生くらいで授業についていくのが辛くなり始めていました。ちなみに高校が付属校なので大学受験はしていません。 数Ⅰ、数A、数Ⅱ、数Bは同じ教材で学習済み。
#やった内容
###1. 関数
いろいろな関数をここで学んでいきます。分数関数と無理関数からです。画像は他サイトから拝借しています。

項目	基本式	少し複雑化	グラフ基本形
分数関数	$y=\frac{k}{x}$	$y=\frac{k}{x-p}+q$ $y=\frac{ax+b}{cx+d}$
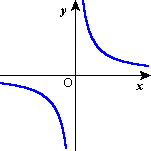無理関数	$y=\sqrt{x}$	$y=\sqrt{ax+b}$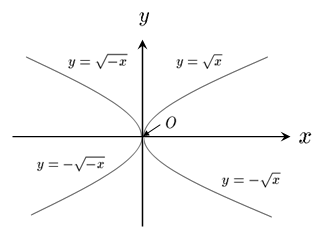

合成関数は多項式で表される関数、分数関数、無理関数、三角関数、指数関数などを組み合わせて作られた関数です。$(g\circ f)(x)=g(f(x))$で表します。
逆関数は通常の関数と逆で$x=f^{-1}(y)$と表します
三角関数は公式がたくさん出てきます。こんなに応用できるなんて正直、すごいね・・・

\sin\alpha\cos\beta=\frac{1}{2}[\sin(\alpha-\beta)+\sin(\alpha-\beta)]\
\cos\alpha\sin\beta=\frac{1}{2}[\sin(\alpha-\beta)-\sin(\alpha-\beta)]\
\cos\alpha\cos\beta=\frac{1}{2}[\cos(\alpha+\beta)+\cos(\alpha-\beta)]\
\sin\alpha\sin\beta=\frac{1}{2}[\cos(\alpha+\beta)+\cos(\alpha-\beta)]\
\sin A+\sin B=2\sin\frac{A+B}{2}\cos\frac{A-B}{2}\
\sin A-\sin B=2\cos\frac{A+B}{2}\sin\frac{A-B}{2}\
\cos A+\cos B=2\cos\frac{A+B}{2}\cos\frac{A-B}{2}\
\cos A-\cos B=-2\sin\frac{A+B}{2}\sin\frac{A-B}{2}\

三角関数は別記事[「基礎数学公式一覧【三角関数】」](http://qiita.com/FukuharaYohei/items/398763e4c4b4ec03f17f)でまとめました。
###2. 極限
####数列の極限
数列の極限は無限数列{$a_n$}の$n$が限りなく大きくなた時の$a_n$についてです。
**収束はある定数に限りなく近づくこと**で下記のように表し、$\alpha$ を**極限値**と言います。

>```math
\lim_{n\rightarrow\infty}a_n=\alpha\\

**収束しない場合に、数列は発散します。**正の無限大または負の無限大に発散します。

\lim_{n\rightarrow\infty}a_n=\pm\infty\

また、その両者でもない**振動**というパターンもあります($a_n=(-1)^n$のような場合)。
####関数の極限
収束、発散に関する考え方は数列の場合と同じです。ただ、関数なのでパターンが増えます。指数関数・対数関数・三角関数などでの極限を学びました。
**極限は、統計の根底にある重要な考え**だと考えています。限りなく試行回数を多くしたと考えた場合、どうなるかです。

###3. 微分法
####微分法
微分は別記事[「基礎数学公式一覧【微分】」](http://qiita.com/FukuharaYohei/items/5fe776fa863a43bf9b72)でまとめました。
数学Ⅱに続く微分です。徐々に難しくなってきます。以下のような公式を覚えます。

>```math
[f(x)g(x)]'=f'(x)g(x)+f(x)g'(x)\\
\left[\frac{1}{g(x)}\right]'=-\frac{g'(x)}{[g(x)]^2}\\
\left[\frac{f(x)}{g(x)}\right]'=-\frac{f'(x)g(x)+f(x)g'(x)}{[g(x)]^2}\\
\frac{dy}{dx}=\frac{dy}{du}\frac{du}{dx}\\
\frac{dy}{dx}=\frac{1}{\frac{dx}{dy}}\\

####いろいろな関数の導関数
様々な関数の導関数を学びます。正直、理解することはできるのですが、完全に消化して覚えるレベルまではいけませんでした・・・時間をかければいけるかもしれませんが、その調子でやるといつに終わるかわからないので、取り急ぎ先に行きました。
まずは、三角関数の導関数です。

(\sin x)'=\cos x,::(\cos x)'=-\sin x,::(\tan x)'=\frac{1}{cos^2 x}

つぎに対数関数の導関数です。ここで正規分布の式にも出てくる$e$がでてきます。$e$は対数関数の極限値で、下の式で表します。

>```math
\lim_{t\rightarrow0}(a+t)^{\frac{1}{t}}=e\\

そして、対数関数の導関数は$(\log x)'=\frac{1}{x'}$, $(\log_a x)'=\frac{1}{x\log a}$ です。指数関数の導関数は$(e^x)=e^x$です。
###4. 微分法の応用
####関数のグラフ
微分を関数のグラフという観点から使います。例えば、曲線$y=f(x)$の点($a, f(a)$)における接線の方程式は、$y=f'(a)(x-a)+f(a)$となります。また、微分が関数の傾きになるという性質から関数の増減や極大・極小について学びます。

####いろいろな応用
今まで学んだ微分の応用として、指数関数($y=xe^{-x}$など)の最大値・最小値を求めたり、不等式の証明をしたり、方程式の解を求めたりします。正直、難しかったです

###5. 積分法
####不定積分
関数$f(ax+b)$の積分としてとして$\int f(ax+b)dx=\frac{1}{a}F(ax+b)+C$を覚えます。また、置換積分法として$\int f(x)dx=\int f(u(t))\frac{dx}{dt}dt$を学びます。
部分積分法としては$\int f(x)g'(x)dx=f(x)g(x)-\int f'(x)g(x)dx$も学びます。これ以外にも三角関数の公式や部分分数分解を応用して積分します。
####定積分
不定積分で学んだ置換積分法と部分積分法を定積分でも使います。
###6. 積分法の応用
####面積と体積
数学Ⅱで積分を使って図形の面積を求めることはやりましたが、数学Ⅲでは体積も計算します。円錐、角錐、回転体の体積を計算します。
####定積分のさまざまな性質
定積分の性質を使って不等式や数列の証明をします。また、区分求積法という考え方で面積や体積を求める方法も学びます。
#感想
正直、理解度が足りなくて消化不良感が残りました。公式を覚えずに前に進んでいるので、数学Ⅱの公式のページを見ながら問題を解いていました。数学のテストをするわけでもないので、考え方を理解したら、暗記をせずにどんどん進んでいます。もし、そのやり方で後々困るようならばまた戻ればいいと今は考えています。
消化不良感こそありながらも、一方で達成感もありました。今までよくわからなかったネイピア数($e$)も出てきて、極限も学習しました！この知識が役に立つことを願い、数学Cへと続きます。