目次
ベクトルの外積とは
下記3つの視点で説明します。
- 成分表示
- 公式
- 図形的意味
成分表示
2つのベクトルa = (a1,a2,a3) とb = (b1,b2,b3) があるとき、下記が成分(外積)となります。
外積とはベクトル量なので、成分で表すことができます。
ちなみに内積はスカラー量です。
(a2b3-a3b2, a3b1-a1b3, a1b2-a2b1)
なんかややこしいですが、下記のようにたすき掛けをするイメージです。
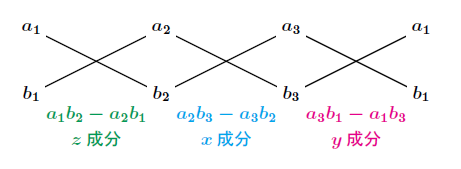
出典:受験の月
公式
外積の大きさは下記の公式で求められます。
|a→×b→| = |a→||b→|sinθ
内積は、a→・b→このように「・」を使って表しますが、
外積は、a→×b→このように「×」を使って表します。
図で解説
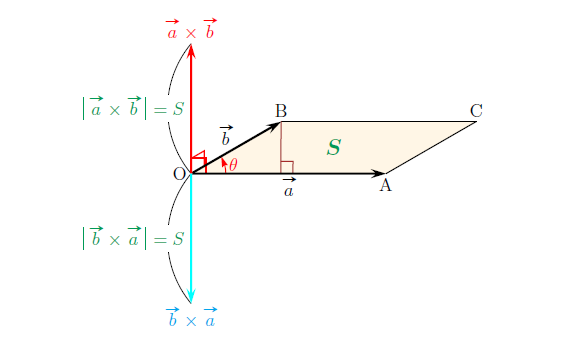
出典:受験の月
a→、b→両方と垂直で、a→からb→方向へ右ねじを回したときに、ねじが進む方向が外積、
上図でいうと、a→×b→の外積は上方向のベクトルS、b→×a→の外積は下方向のベクトルSとなります。
また、図と公式を見るとわかりますが、外積の大きさは、a→とb→を辺とする平行四辺形の面積と同じになります。
|b→|sinθは、a→に対して直角に引いた線の高さと同じになるので、(参考)
平行四辺形の面積を求める公式と、ベクトルの外積を求める公式の内容が等しくなります。
平行四辺形の面積 = 底辺 × 高さ = |a→||b→|sinθ = |a→×b→|
[参考]
受験の月
塾講師STATION
[関連記事]
プログラマーのための数学 - 目次