目次
ベクトルの内積とは
ベクトルの内積とは2つのベクトルの要素を順番にひろって、それらを掛け合わせたものを全部足したもののこと。スカラー積とも呼ばれる。
a→・b→ = a1b1 + a2b2 + a3b3 + ・・・ = Σ[i=1 to n] x[i]y[i]
内積は、a→・b→このように「・」を使って表します。
外積は、a→×b→このように「×」を使って表します。
- 平面ベクトルの場合
a→ = (a1, a2)
b→ = (b1, b2)
a→・b→ = a1b1 + a2b2
- 空間ベクトルの場合
a→ = (a1, a2, a3)
b→ = (b1, b2, b3)
a→・b→ = a1b1 + a2b2 + a3b3
- a→・b→のなす角が90°のとき
a→・b→ = 0
公式
a→,b→のなす角をΘとするとき、下記の公式で内積を求められる。
0°< Θ < 90°
a→・b→ = |a→| |b→|cosθ
証明の仕方を知りたい方はこちら
内積の値の幾何学的検討
図で解説
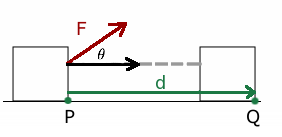
出典:http://d.hatena.ne.jp/Zellij/20130216/p1
左の箱にFの力が加えられたとき、箱はd進む。このとき、この箱になされた仕事は、Fとdの内積と等しいという。
ヨットの例
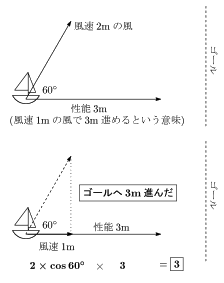
出典:http://naop.jp/topics/topics14.html
風速1mの風で3m進むヨットがあるとする。
ヨットの進行方向に向かって60°の方向へ風速2mで風が吹いたとする。
この場合、ゴールに進むのに役立つ風は1mしかない。(2×cos60°=1)
b→という風は,a→の方向に1m分の仕事をしたということになる。
この「1m」という数値がa→とb→の内積である。
bが90°のとき
bが90°の風ではヨットは進まないので、
内積は 2×cos90°×3より「0」。
「垂直ならば内積が0」
90°より大きい風が吹いた場合は、ヨットはマイナスに進む。
まとめ
a→・b→ = |a→| |b→|cosθ
|b→|cosθという部分は、b→が,a→の方向にどれだけの影響を与えるかということを意味している。
[参考]
KIT数学ナビゲーション
Hatena::Diary
naop.jp
[関連記事]
プログラマーのための数学 - 目次