0.ざっくり言うと
- 前回の記事(RNNにsin波を学習させて予測してみた)の続き。
- 様々なハイパーパラメータを調整して、どのような結果になるかを実験した。
- ハイパーパラメータの調整は難しい!
1. 構成
前回の記事と基本的には同じネットワーク構成を使っています。また、ハイパーパラメータは『3.3. ハイパーパラメータ』に示した値を基本的な値としています。
| 変数名 | 意味 | 値 |
|---|---|---|
num_of_input_nodes |
入力層のノード数 | 1 ノード |
num_of_hidden_nodes |
隠れ層のノード数 | 2 ノード |
num_of_output_nodes |
出力層のノード数 | 1 ノード |
length_of_sequences |
RNNのシーケンス長 | 50 ステップ |
num_of_training_epochs |
学習の繰り返し回数 | 2,000 回 |
num_of_prediction_epochs |
予測の繰り返し回数 | 100 回 |
size_of_mini_batch |
ミニバッチあたりのサンプル数 | 100 サンプル |
learning_rate |
学習率 | 0.1 |
forget_bias |
(よく分かっていません) | 1.0 (デフォルト値) |
2. ソースコード、ノートブック
学習・予測に使用したソースコード、学習データを生成したノートブック、結果のチャート化に使用したノートブックなどは、GitHubで公開しています。
具体的なソースコード、値などはそちらを参照ください。
3. ハイパーパラメータの調整
3.1. num_of_hidden_nodes: 隠れ層のノード数
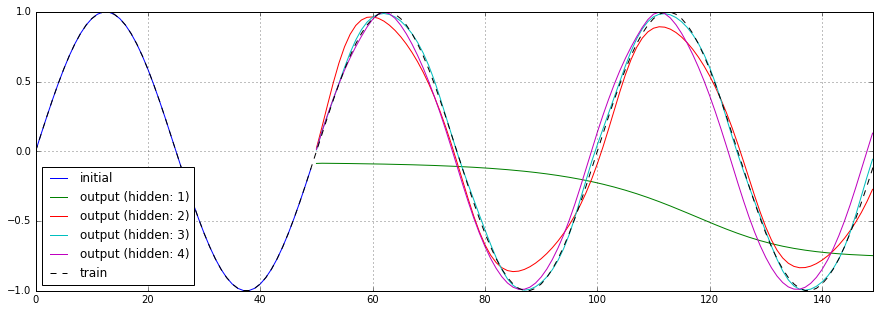
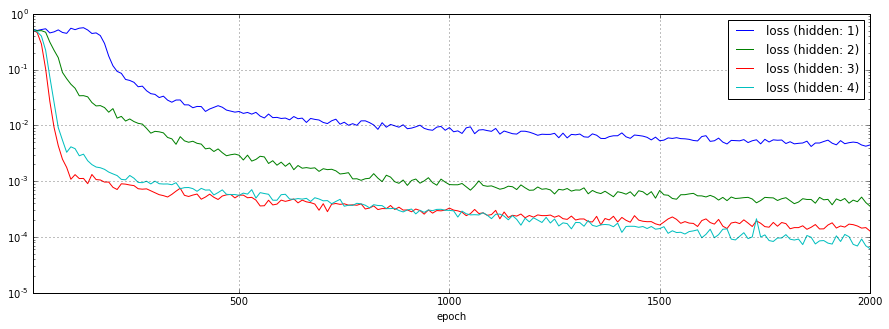
隠れ層のノード数を1〜4と変化させた場合の予測結果、損失関数のチャートを以下に示します。
隠れ層のノード数が1の場合、まったく予測できていない事がわかります。また、隠れ層のノード数が多ければ、必ずしもよい結果を得られるわけでもなさそうです。
損失関数のチャートを見てみると、隠れ層のノード数が多いほど、最終的な損失は少なくなっています。
| No | 隠れ層のノード数 | 学習・予測時間 |
|---|---|---|
| 1 | 1 |
3m53.845s |
| 2 | 2 |
3m30.844s |
| 3 | 3 |
4m36.324s |
| 4 | 4 |
5m30.537s |
3.2. length_of_sequences: RNNのシーケンス長
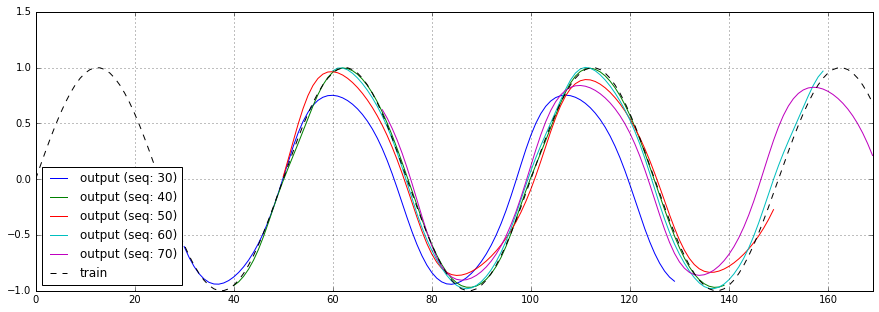
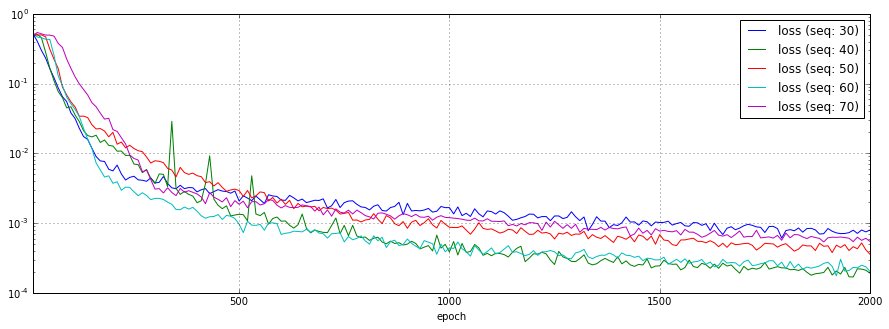
RNNのシーケンス長を30、40、50、60、70と変化させた場合の予測結果、損失関数のチャートを以下に示します。
今回の学習データは1サイクル50ステップのsin波ですが、1サイクル分を下回っても十分予測できている事が分かります。
| No | RNNのシーケンス長 | 学習・予測時間 |
|---|---|---|
| 1 | 30 |
2m29.589s |
| 2 | 40 |
2m58.636s |
| 3 | 50 |
3m30.844s |
| 4 | 60 |
4m25.459s |
| 5 | 70 |
5m38.550s |
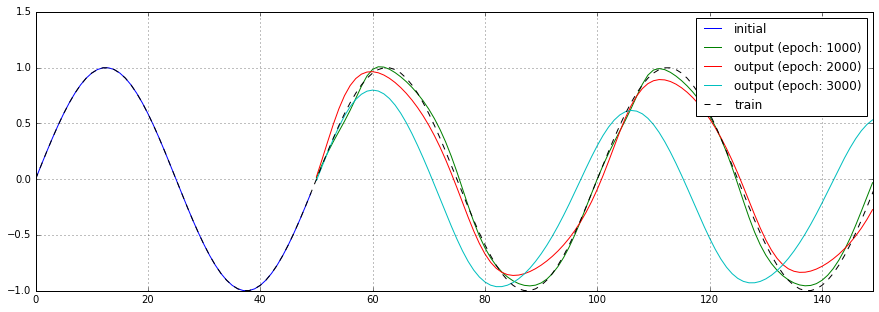
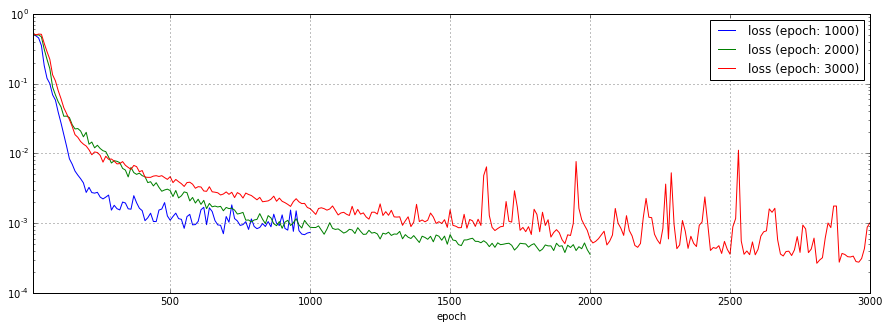
3.3. num_of_training_epochs: 学習の繰り返し回数
学習の繰り返し回数を1,000回、2,000回、3,000回と変化させた場合の予測結果、損失関数のチャートを以下に示します。
3,000回のケースでは、1,600回を越えた辺りから損失関数の結果が振動しています。予測結果も芳しくありません。
| No | 学習の繰り返し回数 | 学習・予測時間 |
|---|---|---|
| 1 | 1,000回 | 2m10.783s |
| 2 | 2,000回 | 3m30.844s |
| 3 | 3,000回 | 6m17.675s |
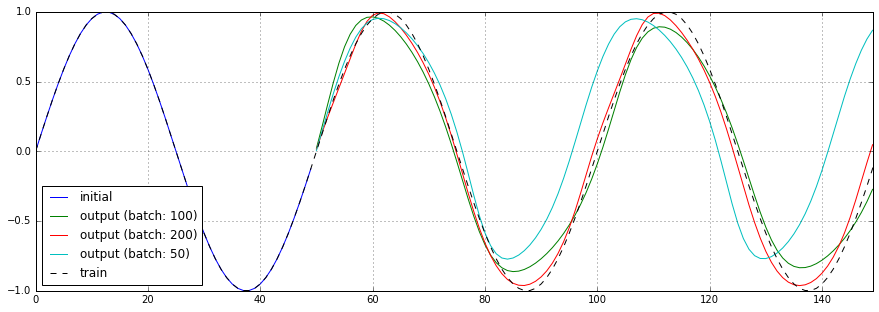
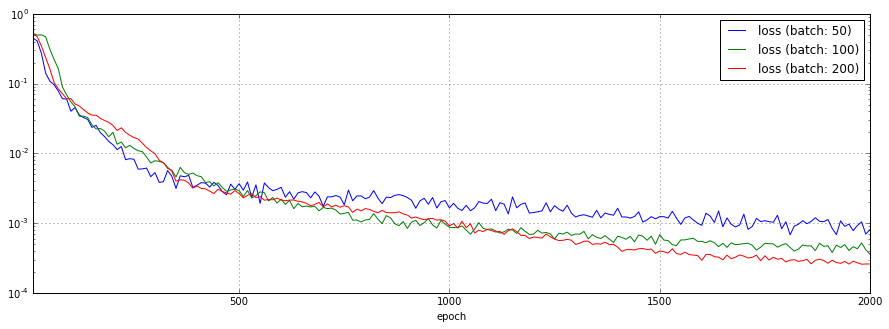
3.4. size_of_mini_batch: ミニバッチあたりのサンプル数
ミニバッチあたりのサンプル数を50、100、200と変化させた場合の予測結果、損失関数のチャートを以下に示します。
顕著な差こそありませんが、基本的にはサンプル数が多い方が良い結果を得られている感じです。
| No | ミニバッチあたりのサンプル数 | 学習・予測時間 |
|---|---|---|
| 1 | 50 |
4m25.032s |
| 2 | 100 |
3m30.844s |
| 3 | 200 |
4m59.550s |
3.5. learning_rate: 学習率
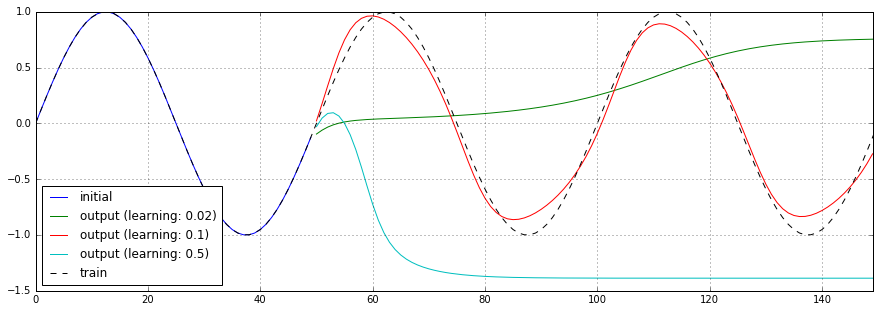
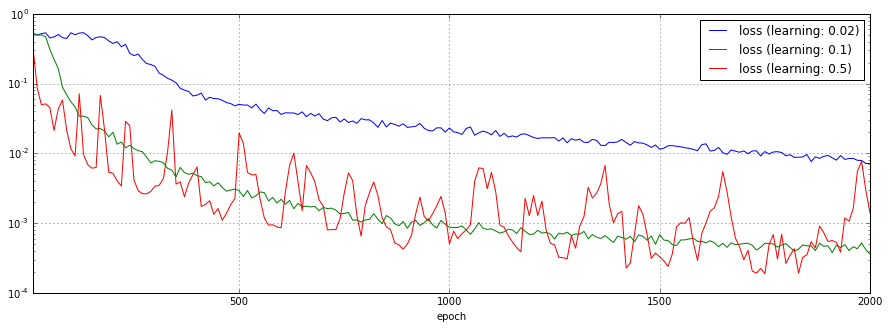
オプティマイザに渡す学習率を0.02、0.1、0.5と変化させた場合の予測結果、損失関数のチャートを以下に示します。
学習率0.02、0.5のケースではまともに予測できていません。また、学習率0.5のケースでは、学習直後から損失関数の結果が振動しています。
| No | 学習率 | 学習・予測時間 |
|---|---|---|
| 1 | 0.02 |
3m46.852s |
| 2 | 0.1 |
3m30.844s |
| 3 | 0.5 |
4m39.136s |
3.6. forget_bias
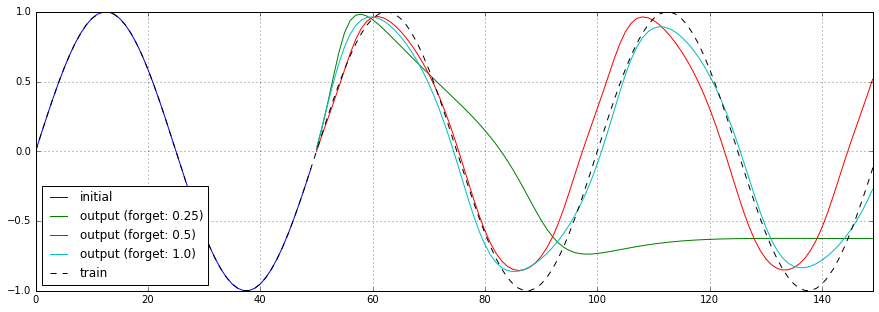
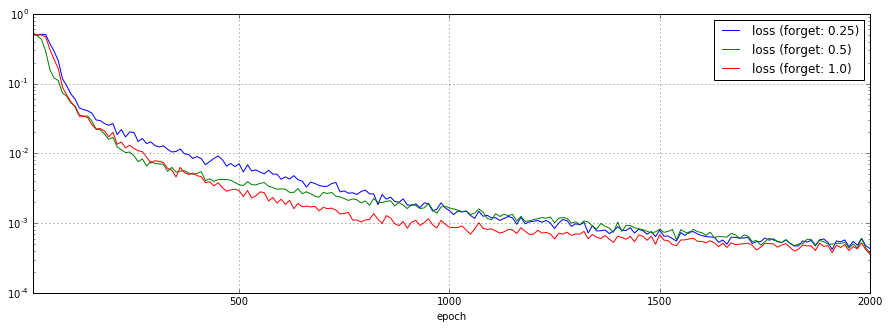
実際の所、よく意味が分かっていないBasicLSTMCellのforget_biasパラメータを0.25、0.5、1.0(デフォルト値)と変化させた場合の予測結果、損失関数のチャートを以下に示します。
0.25のケースではまともに予測できていません。
| No | forget_bias | 学習・予測時間 |
|---|---|---|
| 1 | 0.25 |
4m27.725s |
| 2 | 0.5 |
4m27.089s |
| 3 | 1.0 |
3m30.844s |
3.7. オプティマイザ
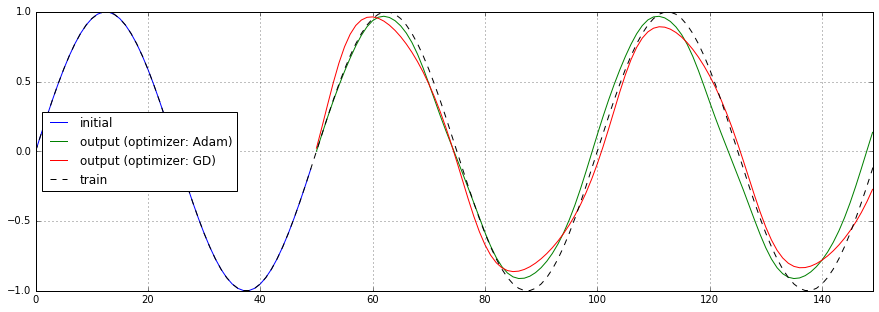
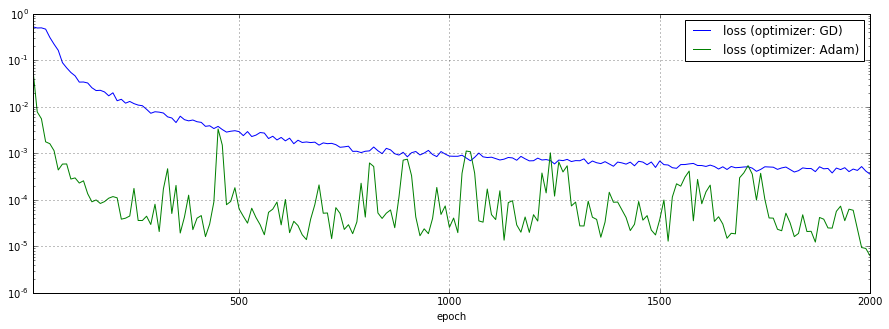
最適化に使用するオプティマイザをGradientDescentOptimizerからAdamOptimizerに切り替えた場合の予測結果、損失関数のチャートを以下に示します。
AdamOptimizerの方が損失の低下が早く、最終的な値が低いようですが、激しく振動しています。学習の止め時が難しいですね。
| No | オプティマイザ | 学習・予測時間 |
|---|---|---|
| 1 | GradientDescentOptimizer |
3m30.844s |
| 2 | AdamOptimizer |
4m46.116s |
3.8. RNNセル
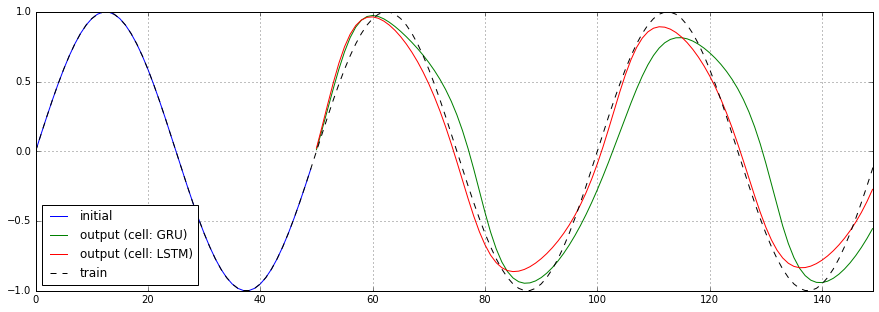
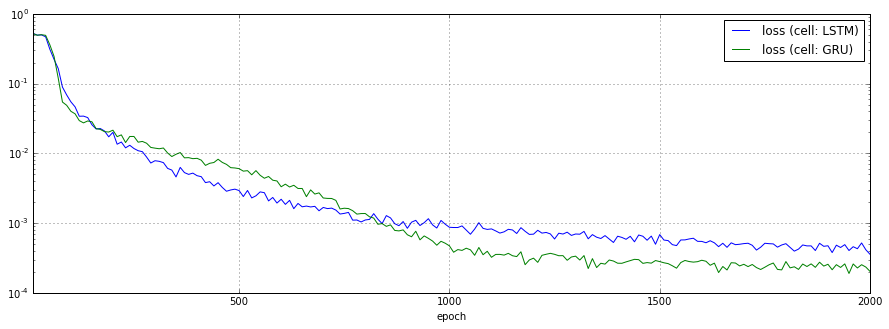
RNNセルをBasicLSTMCellからGRUCellに切り替えた場合の予測結果、損失関数のチャートを以下に示します。
あまり顕著な差は見られませんでした。
| No | RNNセル | 学習・予測時間 |
|---|---|---|
| 1 | BasicLSTMCell |
3m30.844s |
| 2 | GRUCell |
4m53.831s |
4. 今後の予定
より現実的なデータ(株価、外国為替など)を学習、予測させたらどうなるかを試してみたいと思っています。