※この投稿はシリーズものの一部です。
part301 <-[part0](http://qiita.com/yuusei/items/49a63f4402afc66243e6)->[part303]GW中投稿できるといいな
故あって、いつものシリーズのスケジュールを一気に飛ばし、
ルベーグ積分のイメージ(数学的な定義はほどほどに)について書く必要が出たので、一気に飛ばして301とします。落ち着いたところでちゃんとナンバリングし直す予定です。
4章 確率過程を理解する為の基礎概念
この章ではランダムウォークなどから派生する確率過程を理解するため、入門として測度やルベーグ積分、あるいは無限級数がらみでフーリエ変換からの大数の法則についてお話ししたいと思います。
4.1 確率空間 一旦スキップ
4.2 独立性 一旦スキップ
4.3 ルベーグ積分 該当エントリ
4.4 区分求積法
2次元上の区分求積法とは、
回りくどい表現をすると連続な関数を長方形の集まりとして表現し、長方形の面積を合計したものを連続な関数と$x$軸の間の面積を求めるです。
ぶっちゃけると高校でやるlimとシグマの合わせ技です。
前回のように絵で描くと、
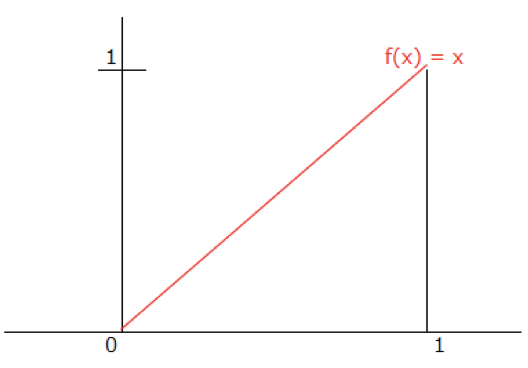
$f(x) = x$に対して$0 \leq x \leq 1$の範囲で関数とx軸の間の面積を求める事を考えます。
(わかると思いますが、面積は 1/2=0.5 です)
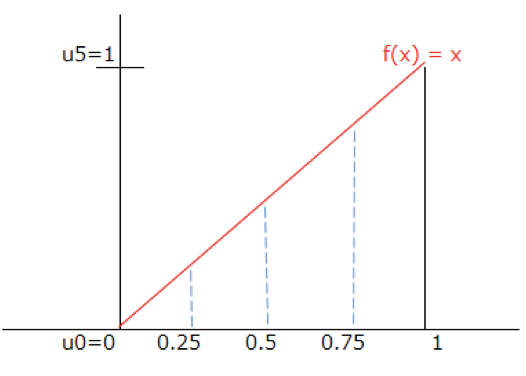
これを、$n = 4$として、$x$軸を$1/n = 1/4 = 0.25$ 間隔に区切りましょう。
これで長方形が描けます。
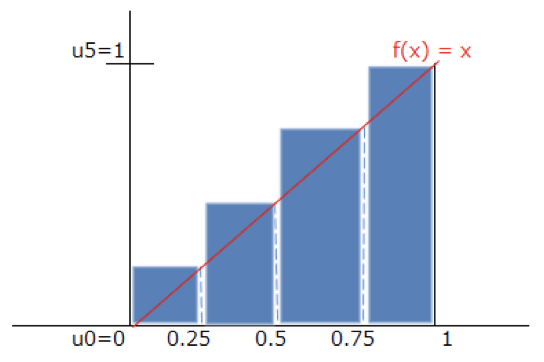
この面積を$f(x)$と$x$軸の間の面積として採用するのが、区分求積法の第一段階です。
次の段階として、考えるのが**「$f(x) = x$ラインより上にはみ出している面積が気持ち悪い」**です。
これさえなくなれば長方形の面積の合計と被積分関数$f(x) = x$の面積は一致するのに・・・
さてどうしましょう?
昔の人は考えました。$n$を大きくして(つまり、0.25間隔ではなく、もっと小さな間隔で)同じ事をすればいいんじゃないかと。
例えば、$n= 8$でやってみましょう。
注)こういった事を考える場合に$x$軸は等間隔で分割する暗黙のルールがあるため、ここでの分割は $2 \rightarrow 4 \rightarrow 8$のように、$n= 2^k$でしか行いません。
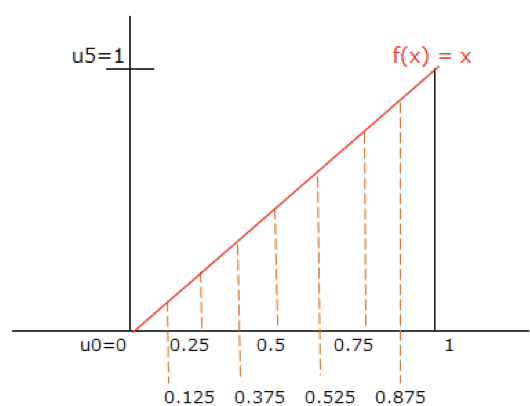
0.125間隔。エクセルで描く図としては結構細かいです。
長方形を当てはめましょう。
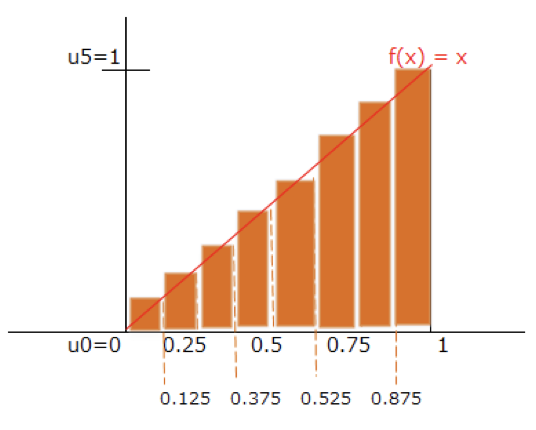
$f(x) = x$よりも上にある部分の面積が少なくなった気がしませんか?
$n=4$と$n=8$を重ねてみましょう。
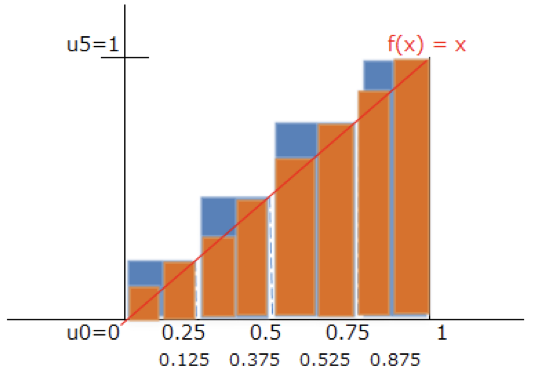
青い四角形が見えているところが、分割区間を細かくする事で除かれた余剰面積ですね。
そこだけ取り出すとこんな感じ?
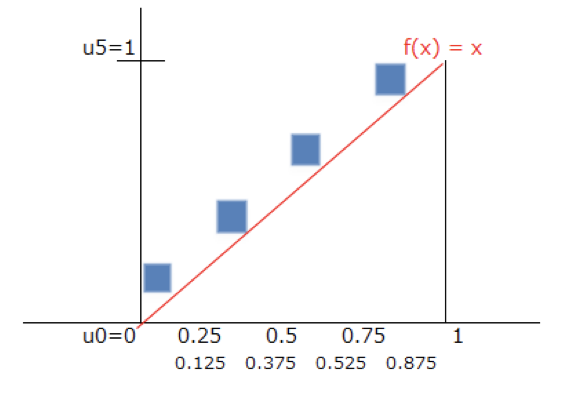
このように、余剰範囲は $n=2^k$で細かく分割していくと、いつか($n \rightarrow \infty $)では、
長方形の面積の合計と、$f(x) = x$と$x$軸に囲まれた範囲が一致するとおもわれます。
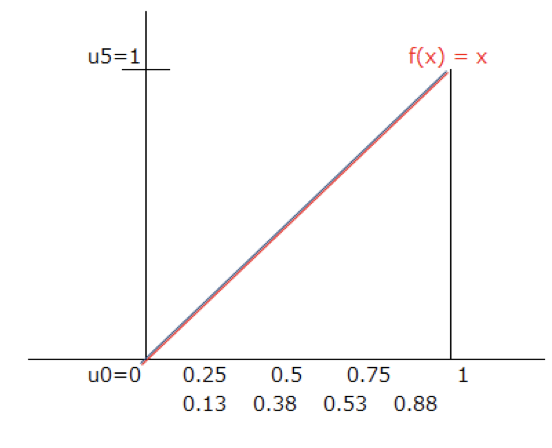
これが区分求積法の考え方です。数式にすると、
\begin{eqnarray}
(求めたい部分の面積 &=& \lim_{n \rightarrow \infty } \sum_{k}^{n} (分割が n = 2^k の長方形の面積) \\
&=& \lim_{n \rightarrow \infty } \sum_{k}^{n} \{ f(\frac{k}{n}) \frac{1}{n} \} \\
&=& \lim_{n \rightarrow \infty } \frac{1}{n} \sum_{k}^{n} f(\frac{k}{n})
\end{eqnarray}
となります。このようにして、分割数を極限に飛ばして上記のような数列の極限で近似するのが区分求積法です。
さて、この区分求積法、リーマン積分でもルベーグ積分でも適用できる便利な方法なんですが、リーマン積分でやるには大きな制約があります。
リーマンでは「長方形で近似している数値が一様収束する」、「被積分関数が連続」と言う二つの(厳密にはなんやかやで三つあるようなんですが)制約があり、これを証明してからでないと積分が存在しなかったりします。
しかしながら、ルベーグ積分ではこのような「一様収束」や「連続」といった部分をスキップして積分ができるようになります。つまり数学科が数列の極限や面積を扱う際に、煩雑な議論をシンプルにできるわけです。理論系の数学科や物理学科の学生には必須。そうでなくても、実務面で新しい関数を使いたい時に、このあたりを考慮して使わないと痛いめ見ることはありそうです。
さて、といった形で区分求積法のイメージを描いてみましたがいかがでしたでしょうか?
次回は数列の極限に絡んだ話で「一様収束」や「連続」を扱おうか、ルベーグ積分を整理するために、さっさと測度論の話に戻るか悩んでいます。まぁ、仕事の中身次第です。それでは!