part301 4章 確率過程を理解する為の基礎概念 〜ルベーグ積分:準備
※この投稿はシリーズものの一部です。
part9 <-[part0](http://qiita.com/yuusei/items/49a63f4402afc66243e6)->part302
故あって、いつものシリーズのスケジュールを一気に飛ばし、
ルベーグ積分のイメージ(数学的な定義はほどほどに)について書く必要が出たので、一気に飛ばして301とします。落ち着いたところでちゃんとナンバリングし直す予定です。
4章 確率過程を理解する為の基礎概念
この章ではランダムウォークなどから派生する確率過程を理解するため、入門として測度やルベーグ積分、あるいは無限級数がらみでフーリエ変換からの大数の法則についてお話ししたいと思います。
4.1 確率空間
一旦スキップ
4.2 独立性
一旦スキップ
4.3 ルベーグ積分
ここでは、高校数学までで教える積分とは別の考え方で定義されたルベーグ積分についてお話しします。
ルベーグ積分の説明については、測度や確率空間を丁寧に定義してから説明する講義が大学でのほとんどを占めているようですが、そうすると何年経っても終わらないので、ここでは
・ルベーグ積分と高校までの積分(リーマン積分)は何が違うのか?
・ルベーグ積分があると何が嬉しいの?
・リーマン積分とは何をやっているのか?(高校数学の確認)
・区分求積法とはなんぞや?(数列の極限の話)
・ルベーグ積分の定義と数列の極限としての面積の考え方
・可測とはなんぞや
などを順番は前後するかもしれませんが、話していきたいと思います。
ルベーグ積分の説明は九州大学のこの講義ノートに詳しく、数式は主にこれを踏襲した形で、図解を交えて説明していきたいと思います。
それでは始めましょう。
4.3.1 ルベーグ積分とリーマン積分は何が違うのか?
これは人によって色々と言葉が変わるのですが、簡単のためにまずは2次元の座標上で$f(x) = x$と言う関数を考えてみましょう。さらに、$x \in [0,1]$ ($x$の取りうる範囲は0〜1)であるとします。
するとこんなよく見知ったグラフが描けますね?
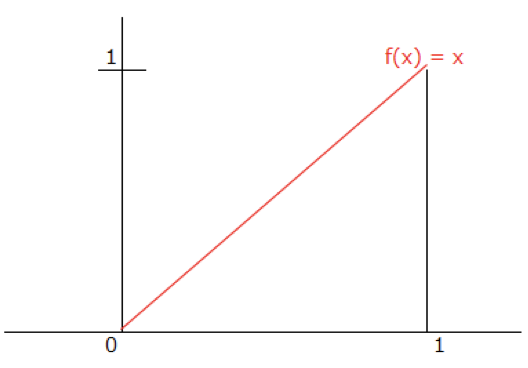
この図をベースとして、$f(x) = x$と$x \in [0,1]$の範囲で囲まれた面積を求める事を考えます。(つまり、$f(x) = x$ を$0 \leq x \leq 1$の範囲で積分する事を考えます。
この時、リーマン積分は*$x$軸を分割*して、面積を求めていたと思います。
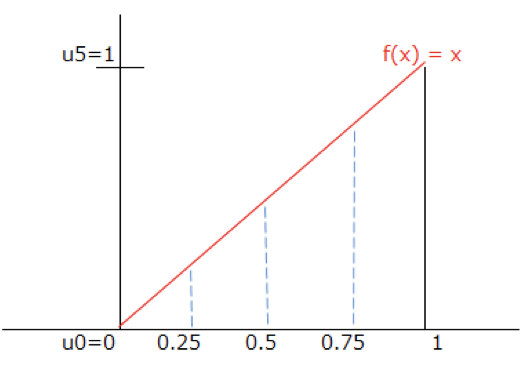
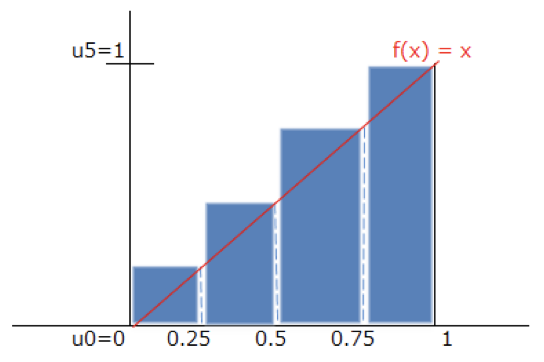
こんな感じ。
これに対して、ルベーグ積分は$y=f(x)$となる*$y$軸を分割*して、面積を求めます。
それでどうやって積分するの???と思った人はまぁ次の図を見てください。
ルベーグ積分は分割した区間ごとに$f(x)$の最大値と最小値を求め、$f(x)$をも区間に分割します。
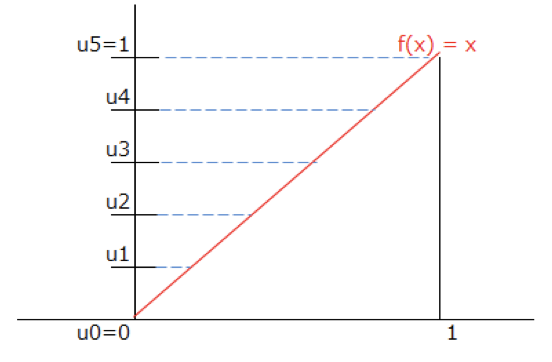
そして、分割した$f(x)$の$x$軸上への射影の長さを使って、リーマン積分の様に面積を求めるのです。
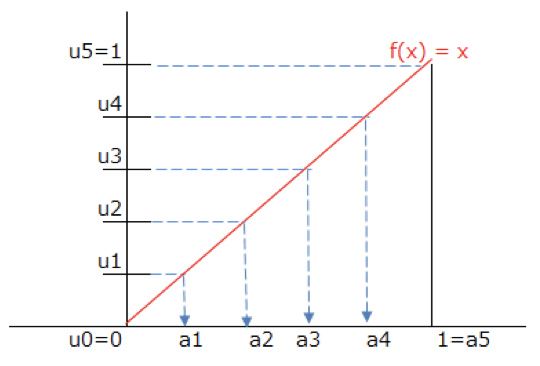
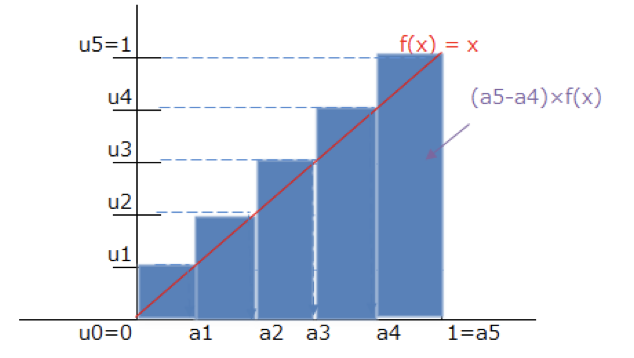
この分割する軸の違いがルベーグ積分とリーマン積分の違いです。人によっては「ルベーグ積分は横に切る」と聞いた事もあるかもしれません。それは、こう言った作業をしているからです。
では、どう数式で定義すると「ルベーグ積分が可能になるのか?」と言う話は、次に譲るとして、
「ルベーグ積分があると何が嬉しいのか?」と言う話をします。
下記の数式で定義された関数を考えます。
(この関数はルベーグ積分の便利さを伝えるためによく引き合いに出され、ディリクレの関数と呼ばれます)
f(x) = \begin{cases}
1 & (xが有理数) \\
0 & (xが有理数でない)
\end{cases}
つまり、こう言った関数です。
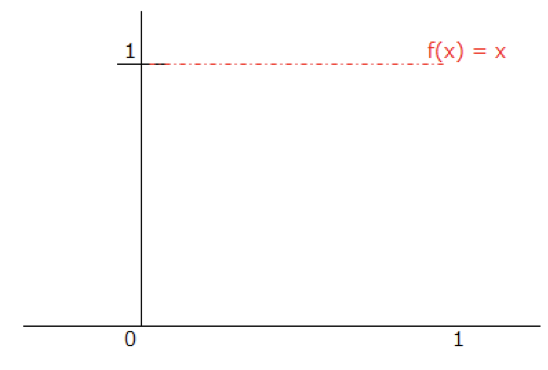
図の中の点線はあくまでイメージです。これは$x$が有理数の時の$fx)$の集まりを表現していて、$f(x)=1$になる値は飛び飛びであるを表現しています。
本来は、こんな感じで$f(x)=1$が下図よりも密に存在しているはずです。
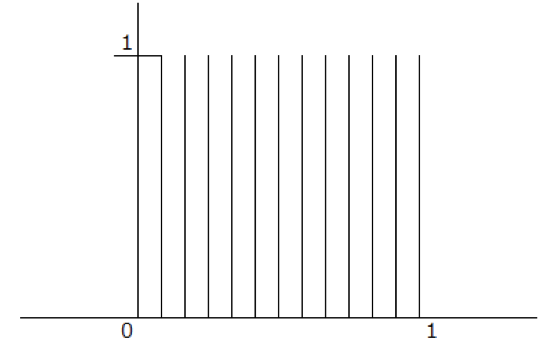
さて、この関数は従来のリーマン積分で考えると、どうしたらいいのでしょうか?
多くの人が直感的には「$x$軸は幅が 0 の点によって分割されるので、この関数の積分は0である」と言うと思います。ですが、そう言いつつも何か心にモヤモヤができるかと思います。そのモヤモヤとは幅が0の点によって分割されると言う箇所です。
幅が 0 の点って線分を「分割」できるのか?
ここに多くの人のモヤモヤがあるはずです。
ですが、ルベーグ積分を使えばこのモヤモヤは晴れます。
なぜなら、
ディリクレ関数の $f(x) = 1$ となるところは、$x$軸の写像は”0”となる。
からで、つまり
「幅が0」と言う言語の罠から抜け出し「$f(x) = 1$でも$x=0$になるんだから積分は 0 だよね」
と言うオチがつくからです。これがルベーグ積分が**$f(x)$と$x$軸との間の面積を求める方法**として、リーマン積分と並んで重宝される理由です。
どうでしたか?ルベーグ積分があると嬉しい理由、なんとなくでもわかりましたか?
このルベーグ積分は確率空間や確率過程を支える一つの理論として使われています。
その辺りについて詳しく説明していきたいのですが、その辺りは関数の極限に類似した概念、
「上限」と「下限」、「sup」と「inf」について説明してからでないといけません。
そしてそれらを説明するためには、区分求積法と数列の極限について話していかないといけませんので、そっちを先に進めていきます。それではまた。