前回までに引き続き matplotlib と pandas によるデータ可視化について話を進めていきます。
外部データを可視化する
今回はより実践的なデータとして外部のデータを利用しましょう。この記事の参考にもしている pydata-book のデータをまずダウンロードしてきます。
pydata-book/ch08/tips.csv
https://github.com/pydata/pydata-book/blob/master/ch08/tips.csv
import numpy as np
from pandas import *
import matplotlib.pyplot as plt
tips = read_csv('tips.csv')
# CSV データのクロス集計をおこなう
party_counts = crosstab(tips.day, tips.size)
print( party_counts )
# =>
# size 1 2 3 4 5 6
# day
# Fri 1 16 1 1 0 0
# Sat 2 53 18 13 1 0
# Sun 0 39 15 18 3 1
# Thur 1 48 4 5 1 3
# データを正規化する
party_counts = party_counts.div(party_counts.sum(1), axis=0)
print( party_counts )
# =>
# [4 rows x 6 columns]
# size 1 2 3 4 5 6
# day
# Fri 0.052632 0.842105 0.052632 0.052632 0.000000 0.000000
# Sat 0.022989 0.609195 0.206897 0.149425 0.011494 0.000000
# Sun 0.000000 0.513158 0.197368 0.236842 0.039474 0.013158
# Thur 0.016129 0.774194 0.064516 0.080645 0.016129 0.048387
# 積み上げ棒グラフでプロッティングする
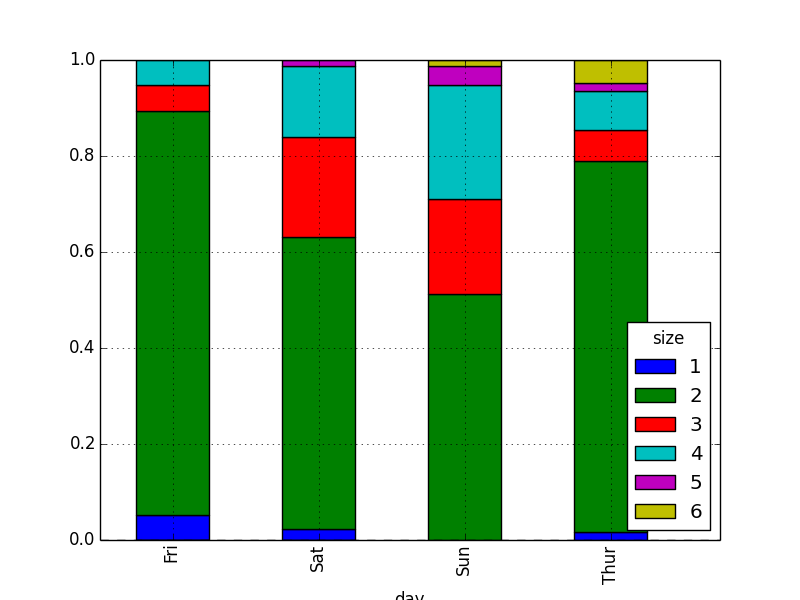
party_counts.plot(kind='bar', stacked=True)
plt.show()
plt.savefig("image.png")
このグラフからは週末 (土曜や日曜) になると人数が多くなるということが読み取れます。 1 人のお客さんは日曜日にはほとんどおらず、 3 〜 4 名程度の家族連れと思われる団体客の割合が明らかに増えています。
ヒストグラムとフィッティング
値の頻度を離散変数としたとき棒グラフはこれを表します。合計金額に対するチップの割合を棒グラフで表してみます。
連続確率分布を正規分布などの確率分布にフィッティングさせることは以前にもガウシアンフィッティングなどを例に説明しました。 カーネル密度推定 (kernel density estimate) プロットを KDE プロットと言います。 plot に kind='kde' を指定することで混合正規分布カーネル密度推定を用いた密度プロットをすることができます。
fig = plt.figure()
ax1 = fig.add_subplot(2,1,1)
ax2 = fig.add_subplot(2,1,2)
tips['tip_pct'] = tips['tip'] / tips['total_bill']
result = tips['tip_pct']
result.plot(kind='kde')
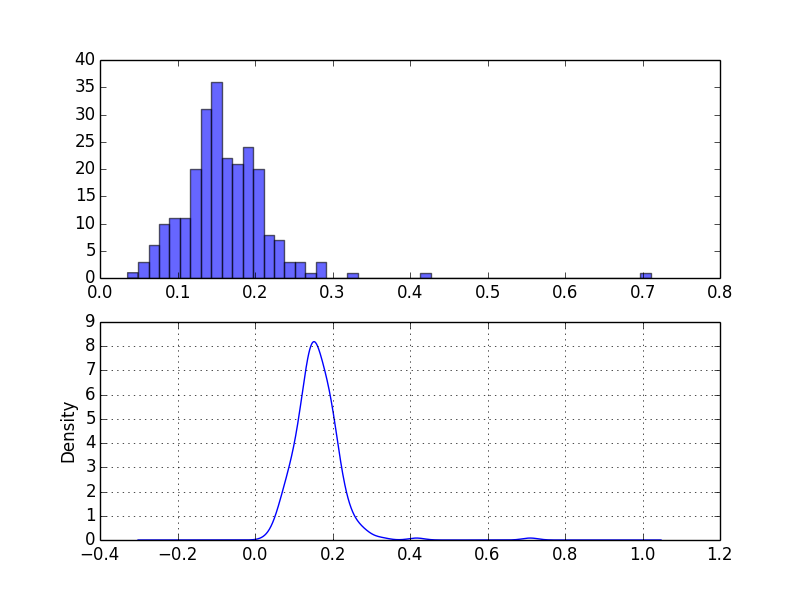
ax1.hist(result, bins=50, alpha=0.6)
plt.show()
plt.savefig("image2.png")
正規化されたヒストグラムの上にカーネル密度推定をプロットすることで、フィッティングのようなことができます。これはよくある手法です。
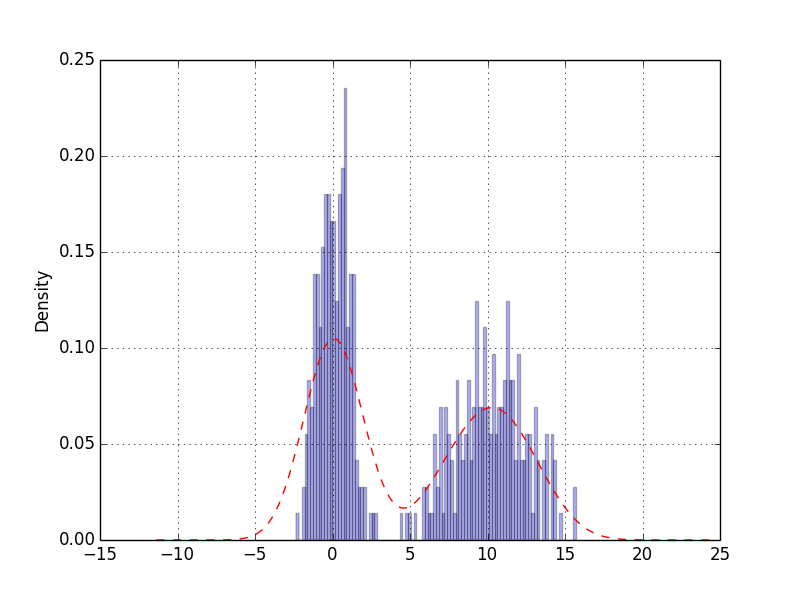
2 つの異なる標準正規分布 N(0,1) および N(10,4) を用いて描いたプロットにフィッティングをしてみます。
fig = plt.figure()
ax = fig.add_subplot(1,1,1)
# 正規分布その 1
comp1 = np.random.normal(0,1,size=200) # N(0,1)
# 正規分布その 2
comp2 = np.random.normal(10,2,size=200) # N(10,4)
# ふたつの正規分布を 1 つのシリーズにする
values = Series(np.concatenate([comp1, comp2]))
print( values )
# =>
# [4 rows x 6 columns]
# 0 -0.305123
# 1 -1.663493
# 2 0.845320
# 3 1.217024
# 4 -0.597437
# 5 0.559524
# 6 0.849613
# 7 -0.916863
# 8 2.705579
# 9 1.397815
# 10 -1.135680
# 11 0.322982
# 12 0.568366
# 13 0.567607
# 14 0.360048
# ...
# 385 15.695692
# 386 8.868396
# 387 8.625446
# 388 5.793579
# 389 8.169981
# 390 8.434327
# 391 10.305067
# 392 11.032880
# 393 8.319812
# 394 9.026077
# 395 9.534395
# 396 4.498352
# 397 12.557349
# 398 7.365278
# 399 11.065254
# Length: 400, dtype: float64
# 棒グラフを描く
values.hist(bins=100, alpha=0.3, color='b', normed=True)
# カーネル密度推定
values.plot(kind='kde', style='r--')
plt.show()
plt.savefig("image3.png")
参考
Pythonによるデータ分析入門――NumPy、pandasを使ったデータ処理
http://www.oreilly.co.jp/books/9784873116556/