SciPy はたくさんの数学的なアルゴリズムや便利な関数の集合体で NumPy を基礎としその延長線上に作られています。今日はその膨大な SciPy のサブパッケージのうちほんの一部ですがよく使う便利な関数について探索をしていきます。
サブパッケージには次のようなものがあります。これらはそれぞれ from scipy import PACKAGE_NAME といった方法で呼び出すことができます。 (他にもやりかたがあります)
| パッケージ | 内容 |
|---|---|
| cluster | クラスタリングアルゴリズム |
| constants | 物理定数や数学定数 |
| fftpack | 高速フーリエ変換ルーチン |
| integrate | 統合と常微分方程式 |
| interpolate | 補間とスムージングスプライン |
| io | 入力および出力 |
| linalg | 線形代数 |
| ndimage | N 次元処理 |
| odr | 直交距離回帰 |
| optimize | 最適化と根検出ルーチン |
| signal | シグナル処理 |
| sparse | スパース行列と関連したルーチン |
| spatial | 空間データ構造とアルゴリズム |
| special | 特別な機能 |
| stats | 統計的分布と機能 |
| weave | C/C++ 統合 |
筆者の独断と偏見でこのうち特によく使うサブパッケージを選ぶとすると scipy.stats と scipy.linalg です。
統計関数 (scipy.stats)
scipy.stats は統計のためのサブパッケージです。まず、連続確率変数と離散確率変数をカプセル化した 2 つの一般的なクラスがあります。 SciPy にはこれを基にした 80 以上の連続確率変数と 10 以上の離散確率変数に関するクラスがあります。これら主に統計に関するクラスは scipy.stats の下にまとまっています。
連続確率変数に関する共通のメソッドには次のようなものがあります。
| メソッド | 内容 |
|---|---|
| rvs | ランダム変量 |
| 確率密度関数 | |
| cdf | 累積分布関数 |
| sf | 生存関数(1-CDF) |
| ppf | パーセントポイント関数 (CDF の逆) |
| isf | 逆生存関数(SF の逆) |
| stats | 平均、分散、フィッシャーの尖度、尤度 |
| moment | 非中心化積率 |
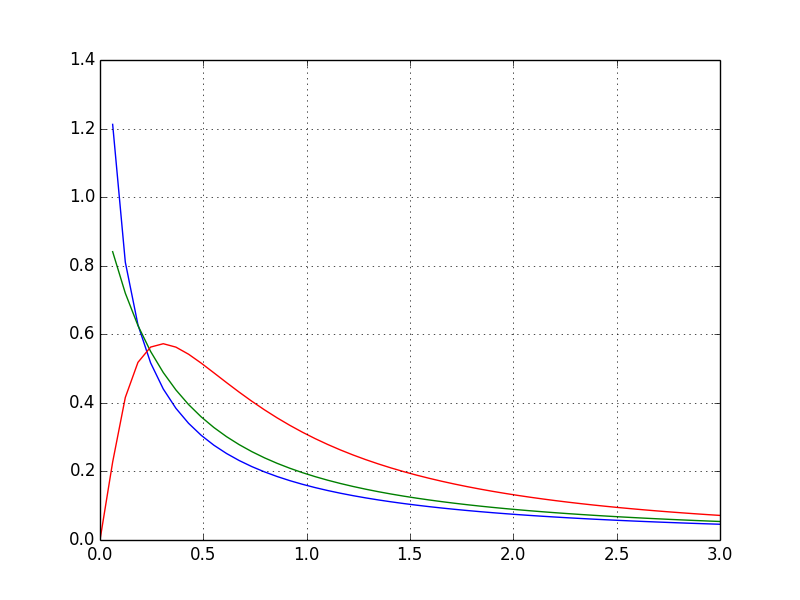
F 分布
おなじみの F 分布です。
from scipy.stats import f # stats から F 分布を呼ぶ
def draw_graph(dfn, dfd):
rv = f(dfn, dfd) # 与えられた 2 つの引数で F 分布を描く
x = np.linspace(0, np.minimum(rv.dist.b, 3))
plt.plot(x, rv.pdf(x))
draw_graph(1, 1)
draw_graph(2, 1)
draw_graph(5, 2)
z 得点
次のように求まります。
x = np.array([61, 74, 55, 85, 68, 72, 64, 80, 82, 59])
print(stats.zscore(x))
# => [-0.92047832 0.40910147 -1.53413053 1.53413053 -0.20455074 0.20455074
# -0.61365221 1.02275369 1.22730442 -1.12502906]
線形代数 (scipy.linalg)
BLAS と LAPACK を利用した非常に高速な線形代数計算をできます。
線形代数ルーチンはすべて 2 次元配列に変換することができるオブジェクトを前提としています。これらのルーチンの出力も基本的に 2 次元配列となります。
x = np.array([[1,2],[3,4]])
linalg.inv(x)
# =>
# array([[-2. , 1. ],
# [ 1.5, -0.5]])
まとめ
SciPy のサブパッケージは膨大な関数を備えていてとても説明しきれるものではありません。興味が出た方は、ぜひオンラインドキュメントを読んでみてください。
またオンラインドキュメントだけで足りない人は、以前に紹介した無料書籍もあわせて参考にすると良いでしょう。