前編を書いたので今回は後編かと思いきや、まったく別の話題で多重回帰分析の話です。
回帰分析は計量経済学などの応用分野の基礎にあたる重要な分析方法で、数値計算と回帰式の当てはめ、統計学的解釈を含みます。以前の重回帰分析では本当に軽く表面をなぞるだけでしたので、今回はもう少し深く掘り下げてみたいと思います。
多重回帰分析の定義
さまざまな経済現象においては必ずしも 1 つの変数が 1 つの要因で決定されるわけではありません。たとえばある家計の食費は、その家計の所得および家族の構成人数で決まるかもしれませんが、食費が所得だけで決まると考えたり構成人員数だけで決まると考えたりするといずれも必要な説明要因を省いていることになります。
一般的な K 変数からなる多重回帰モデルは次のように与えられます。
Y_i = \beta_1 + \beta_2X_{2i} + ... + \beta_kX_{ki} + \mu_i
具体的にデータを追いながら説明していきたいと思います。
回帰分析の対象となるサンプルデータ
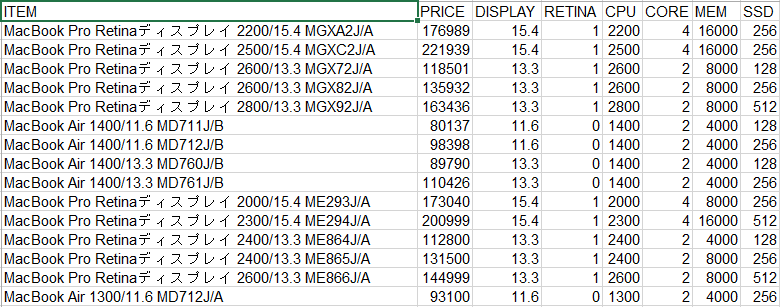
上に挙げたのはアップル製の計算機である MacBook の価格とその性能の一覧です。ここで価格が y であり目的変数 (または被説明変数,従属変数) 、画面のサイズ、 Retina ディスプレイの有無、 CPU の性能、コア数、メモリの容量、ストレージの容量といったものが x であり説明変数 (独立変数) となります。価格を説明する回帰式を求めることが目的です。
一般化線形モデルの表にある通り、多重回帰分析では目的変数、説明変数とも量的データ (数値) であることが前提となります。したがいまして説明変数に質的変数 (カテゴリーデータ) が含まれているとき (この場合は Retina か否かがそれに相当) は数値に変換します。これをダミー変数と言います。なお、ダミー変数には、一時的ダミー、定数項ダミー、係数ダミーがあります。
何かの結果変数を説明するモデルを作るとき説明変数が複数であるものを重回帰分析、同じ目的で説明変数が連続値以外のものを一般化線形モデル (GLM) と言います。
Excel で回帰分析をすると次のように結果を得られます。これは範囲を選択して データ -> データ分析 -> 回帰分析 とクリックするだけなので簡単です。
回帰分析の推定値の解釈
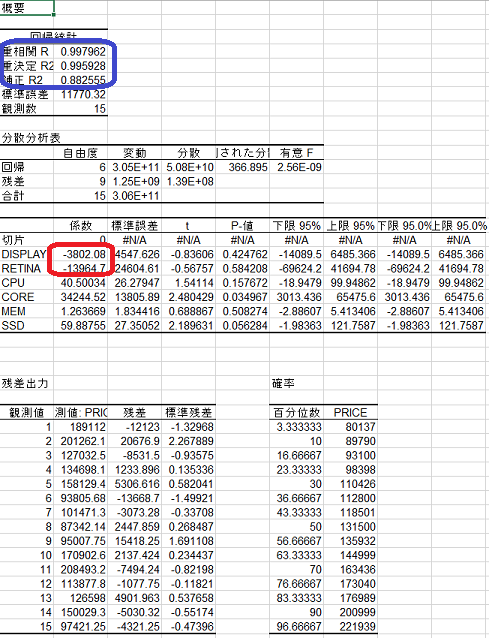
まず最初にみるべき大切な情報は回帰統計です。
重相関係数 R とは回帰式で予測される値と実際の観測値との相関係数です。絶対値が 1 に近いほどよく近似されたモデルであり当てはまりの良い回帰式が得られたということになります。
重決定 R2 は決定係数であり回帰式の説明率です。決定係数は有用な当てはまりの指標ですが 1 つの重要な問題点があります。
決定係数の定義式は次の通りです。
R^2 = 1 - \frac {\sum{\hat{\mu}^2}} {\sum(Y_i - \overline{Y})^2}
すなわち、説明変数を増やせば分子が減少します (減少しないこともあるが増加することは決してない) 。データ数が少ないと決定係数が自由度の影響を受けて必要以上に大きくなることになります。したがって R2 をモデルの選択基準とするには望ましい性質とは言えません。
そこで補正 R2 を見ます。これは自由度修正済み決定係数です。これは次式で定義されます。
\overline{R}^2 = 1 - \frac {\sum{\hat{\mu}^2} / (n-K)} {\sum(Y_i - \overline{Y})^2 / (n-1)}
右辺第 2 項の分母は Y_i の分散の不偏推定量であり、分子は σ^2 の不偏推定量となります。また n-1 と n-K は不偏推定量を求めるために対応する自由度となります。上の式では K の増加と共に n-K も減少するため、説明変数を増やせば分子が必ず減少するとはならなくなります。したがって追加する説明変数の説明率が低いと分子の値が増加することになりますから、説明変数を増やせば増やすほど決定系数が大きくなってしまうという状態から脱します。これが自由度修正済み決定係数の意味です。
この補正 R2 がたとえば 0.5 であればモデルについて半分程度の説明しかできていないことをあらわします。この値が 1 に近いほど良いモデルであるとします。
次に分散分析表を見ます。係数に付いては説明不要でしょう。t 値は大きいほど影響が大きく、 P-値は危険率であり小さいほどその説明変数を用いたときの危険率が低くなります。いずれも切片以外の話です。
多重共線性 (通称・マルチコ)
多重共線性の定義は次の通りです。説明変数が 2 つ (K=3) とすると
Y_i = \beta_1 + \beta_2X_{2i} + \beta_3X_{3i} + \mu_i
これに対し次式のような関係が成り立っているときに説明変数の間に厳密な多重共線性があると言います。
X_{2i} = c + kX_{3i}
c と k は何らかの定数です。これは X_2 と X_3 の間に完全な線型関係が成立している場合です。二変数の標本単相関係数は 1 となります。
一般に言う多重共線性とは上のような厳密な線型関係が成り立っている場合以外だけでなく、説明変数間の相関が高いために推定量の分散が大きかったり t 値が低く統計的に有意な係数推定値が得られなかったりといった問題を指します。主な症状としては次の通りです。
- 推定値の符号が理論とあわない (たとえば高級な部品を使えば使うほど製品の値段が安くなるというふうに)
- 決定係数は大きいのに t 値が小さい
- 観測値を少し増したり説明変数を増減すると、推定値が大きく変動する
具体例を見てみましょう。たとえば上の画像の例では Retina ディスプレイで無いほうが価格が上昇する (ダミー変数の係数がマイナス) ため理論と合致しません。 (直感的におかしいとわかりますよね)
よく用いられる簡単な解決法としては共線関係にある変数のいずれかを取り除くことです。
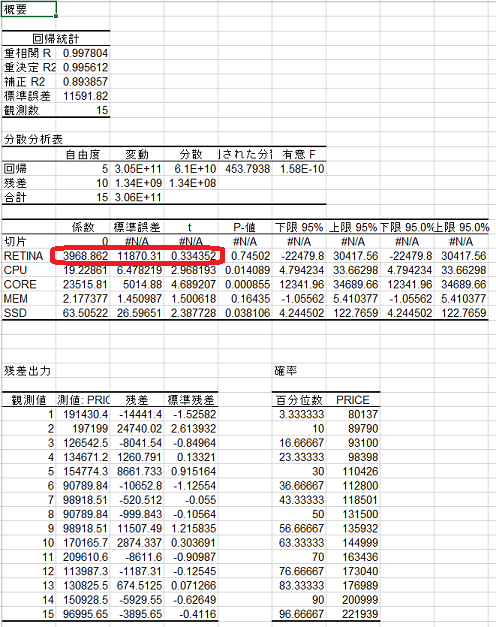
そこでディスプレイのサイズを説明変数から取り除いてみます。
赤字の部分を見ると符号は正になっていますが、係数の大きさに対して t 値が小さすぎます。 (赤色部分)
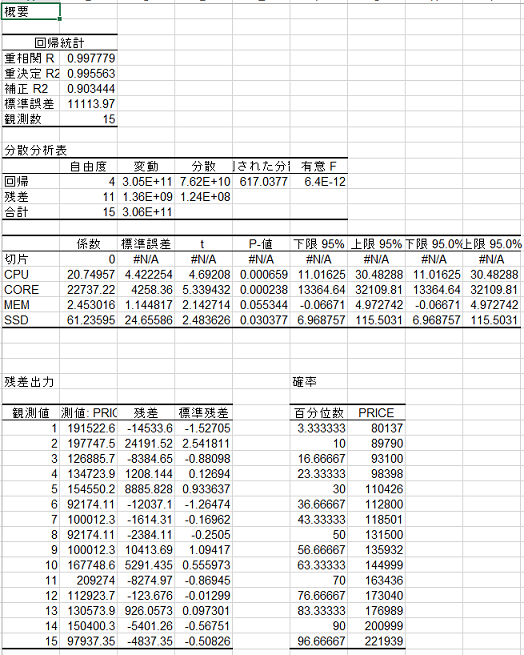
これは有効な変数の選択ではないようです。そこでこれを両方とも除去してみます。
前よりも良くなってきたようですね。
なお、変数を取り除く他に、たとえば複数の変数を合成して新しい説明変数を定義するなどの方法もあります。
変数を投入する際の注意と過不足による影響
どの説明変数を投入するかそれを選択するのは分析者本人となります。投入する説明変数に限りはありませんし、無関係な変数でも共変関係があれば回帰式の説明率は高まります。有意な重相関係数 R が得られたとしても、それはあくまでも共変関係であり説明率が高い式が得られただけにすぎません。因果関係と相関関係は別であることを忘れてはなりません。
回帰分析は、分析者が真のモデルを知っており想定した回帰モデルが正しいという仮定のもとにおこなわれます。推定に先立って分析者がモデルの構造を決めることを定式化と言います。
計量経済学ではある変数をモデルに加えるかどうかは経済理論にしたがって決定します。経済理論が変数の選択に対して明確でないときにこのような選択問題は生じます。 (たとえば輸入関数の推定に国民所得を説明変数とすることは自明だが、金融資産残高も追加するか否か、など)
しかし現実的には誰も真のモデルを知っているわけではありませんから変数の過不足は常に起こり得ます。説明変数の含めるべきか否かを t 検定で調べるといった方法や、より高度な方法も提唱されていますが、いずれも根本的問題を解決するものではありませんので、最終的には分析者の主観に委ねられます。
また変数の選択だけでなく、因果的方向性を証明するにもまた別途の吟味、裏付けが必要です。
前回も書いた通り、人間の判断と洞察が必要になるというわけですね。
なお、説明変数間の寄与の大小は回帰係数ではわかりません。回帰係数の値はそれぞれの変数がとる値の範囲や単位に依存しています。そこで説明変数間の関係を調べるには、全ての変数を平均 0 、分散 1 になるように正規化した時の回帰係数を求めます。これを標準偏回帰係数と言います。これは Excel では表示されませんので別の方法で計算する必要があります。
蛇足
ところで本題とはまったく関係ないのですが、昨日の深夜この内容をブラウザで書いていて完成寸前に Qiita の下書きに保存しようとしたらどうもブラウザの操作が暴走して全選択→カット→保存ってやってしまったらしくほぼ完成間際の文書が真っ白になって保存されてしまうという悲劇に見舞われました。
すでに公開済みの文書なら編集履歴に残るのですが下書きには履歴が無いらしく諦めるしかないということになり心がバキバキに折れました。 Qiita の下書きにたとえ一世代でも履歴があれば助かったのですけれども、結局いちから書き直しました。やはり文書はバージョン管理ソフトウェアで管理した状態でエディタを使って記述するべきですね。 (今後はすべての文書を一貫して Emacs + git で記述します)