はじめに
前回の記事(PyTorchでDeepPoseを実装してみた)ではDeepPoseを実装しつつ,ChainerとPyTorchを比較しました.PyTorchはChainer同様に実装しやすく,性能面では予測はChainerと同程度,学習はChainerよりも早いという結果になりました.今回は性能面について,前回やり残した調査・検証を行い深堀りしていきます.
前回からの実装変更点
前回,PyTorchの学習速度の方がChainerよりも早いことについて,PyTorchではLoss関数のbackward計算の自動微分がCで(ネイティブに)実行されるためではないかという仮設を立てました.今回はそれを検証するために2点,実装を変更しました.
- 乱数の固定
- backwardの明示的実装
乱数を固定するのは検証の再現性を高めるため,backwardを明示的に実装するのはそれによる学習速度の影響を見るためです.
乱数の固定
学習をスタートさせる前に乱数シードを指定する処理を追加しました.なお,ChainerのiteratorはMultiprocessIteratorを使っており,マルチプロセスでの乱数固定はしんどかったので,イテレーション内のData Augmentationは無効にしています.
Chainer
def start(self):
""" Train pose net. """
+ # set random seed.
+ if self.seed is not None:
+ random.seed(self.seed)
+ np.random.seed(self.seed)
+ if self.gpu >= 0:
+ chainer.cuda.cupy.random.seed(self.seed)
# initialize model to train.
model = AlexNet(self.Nj, self.use_visibility)
PyTorch
def start(self):
""" Train pose net. """
+ # set random seed.
+ if self.seed is not None:
+ random.seed(self.seed)
+ torch.manual_seed(self.seed)
+ if self.gpu:
+ torch.cuda.manual_seed(self.seed)
# initialize model to train.
model = AlexNet(self.Nj)
backwardの明示的実装
Extending PyTorchによれば,PyTorchでは,Moduleの微分は自動微分で,Functionの微分は要実装という棲み分けのようです.なので,今回はFunction.backwardを実装すればよさそうです.また,Moduleの入力はVariableで,Functionの入力はTensorである点には注意が必要です.
なお,Functionにはsave_for_backwardという便利メソッドがあって,backward用に変数を取っておけるのですが,計算途中の値についてはサポートしておらず,backward計算に用いるforward計算の途中結果はメンバ変数に格納しました.
PyTorch
def forward(self, *inputs):
x, t, v = inputs
- diff = x - t
+ self.diff = x - t
if self.use_visibility:
- N = (v.sum()/2).data[0]
- diff = diff*v
+ self.N = v.sum()/2
+ self.diff = self.diff*v
else:
- N = diff.numel()/2
- diff = diff.view(-1)
- return diff.dot(diff)/N
+ self.N = self.diff.numel()/2
+ diff = self.diff.view(-1)
+ return torch.Tensor([diff.dot(diff)/self.N])
+
+ def backward(self, *grad_outputs):
+ coeff = grad_outputs[0][0]*2/self.N
+ gx0 = coeff*self.diff
+ return gx0, None, None
検証
前回立てた仮設を検証するため追加で実験を行いました.
なお,検証に用いたデータセット,環境は前回と同じです.
自動微分の影響
PyTorchの自動微分がCで(ネイティブに)実行されることによる学習速度への影響を検証するため,PyTorchの自動微分と明示的微分について,CPU環境とGPU環境でそれぞれ100epoch学習させた時の所要時間を計測しました.
CPU環境
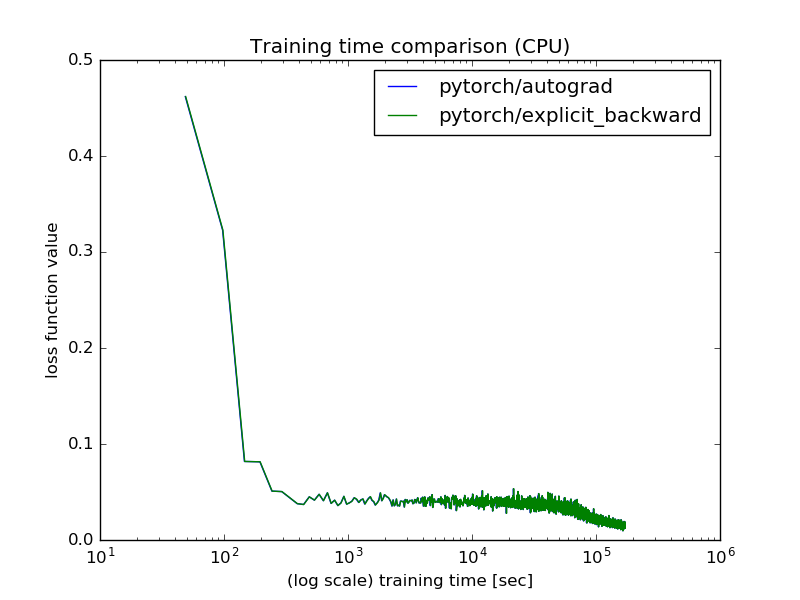
CPU環境では,PyTorchの自動微分も明示的微分も学習時間はほぼ変わらないという結果になりました.
| ライブラリ | 所要時間 [h] |
|---|---|
| PyTorch(自動微分) | 47.6 |
| PyTorch(明示的微分) | 47.6 |
乱数を固定しているため,PyTorchの学習曲線はほぼ重なりました.
GPU環境
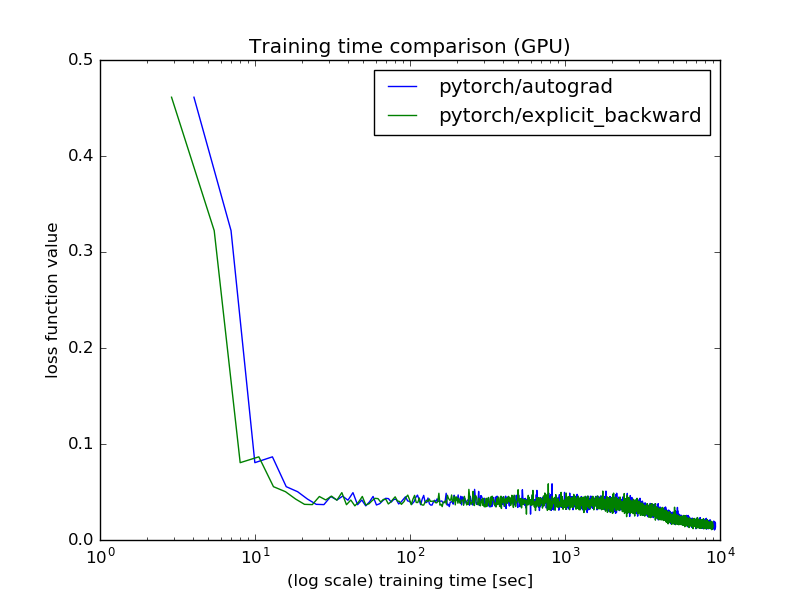
GPU環境では,学習時間はPyTorchの自動微分の方が明示的微分よりもやや遅いという結果になりました.Python実装の方がはやい点は理解が難しいですが,GPUのランダム性に起因する可能性もあり,何度か試すことで結果は変わるかも分かりません.
| ライブラリ | 所要時間 [h] |
|---|---|
| PyTorch(自動微分) | 2.60 |
| PyTorch(明示的微分) | 2.49 |
乱数は固定していますが,GPU起因のランダム性があるため,PyTorchの学習曲線は実装方法により時間軸方向にズレが見れます.
ネットワークレイヤー実装の影響
上記の実験結果を見るに,前回立てた仮設は必ずしも正解ではなさそうです.原因を調査するため,再度コードを眺めていると,ChainerではConvolutionなど各層の実装がPythonであり,PyTorchではCでした.
これが学習時間に対して支配的な影響を与えそうということで,ChainerとPyTorchでLoss関数(ネットワーク込)のforwardとbackward計算に要する合計時間を計測しました.今回は$2^n$のバッチサイズに対して,それぞれ100回計測し平均と分散を計算しました.
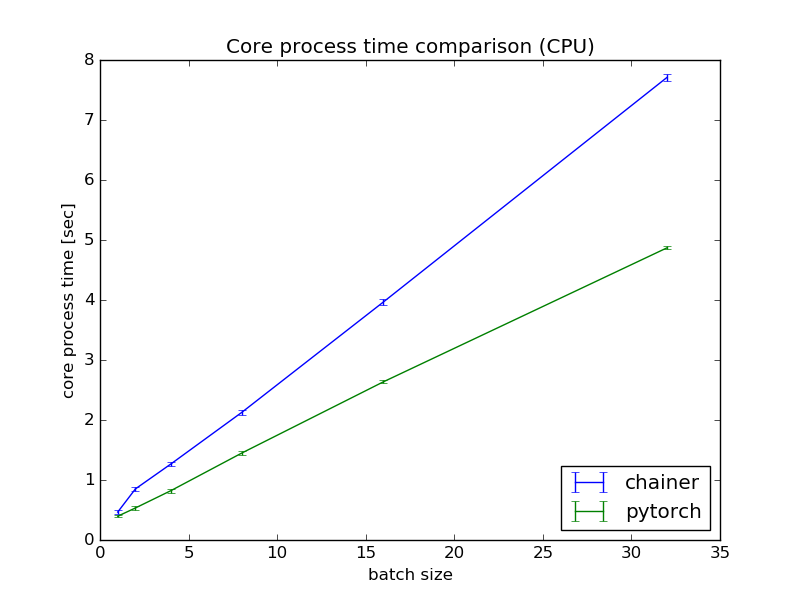
CPU環境
CPU環境では$n=0$の場合は,ほぼ同様な処理時間ですが,$n$の増加に従いPyTorchの方が優位になるという結果になりました.CPU環境でのChainer,PyTorchの1epoch平均の学習時間がそれぞれ8.2[sec],5.0[sec]であることを踏まえると,上記仮設は妥当そうです.
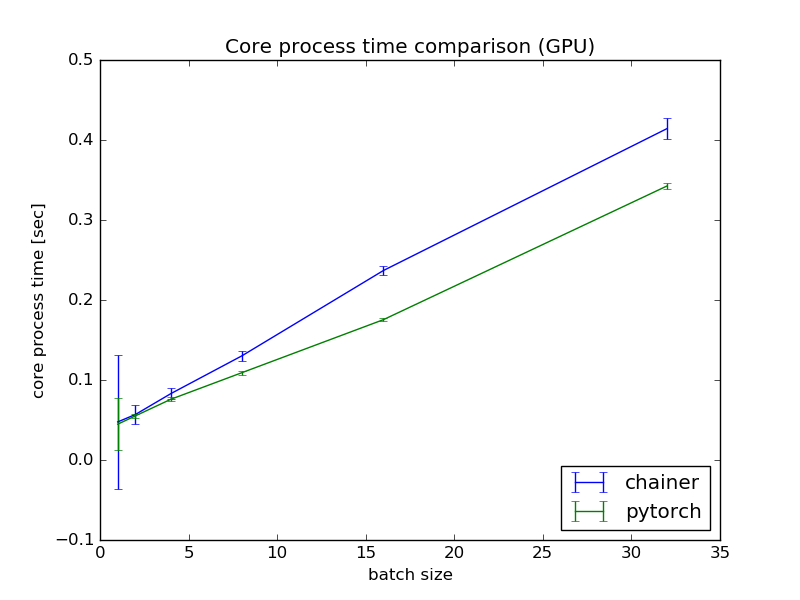
GPU環境
GPU環境でも,CPU環境と同様,$n$の増加に従いPyTorchの方が優位になるという結果になりました.GPU環境でのChainer,PyTorchの1epoch平均の学習時間がそれぞれ0.45[sec],0.28[sec]であることを踏まえると,上記仮設は妥当そうです.
まとめ
前回立てた「PyTorchの学習時間がChainerよりも早いのは,Loss関数のbakcward計算がCで(ネイティブに)実行されるためである」という仮説は半分正解で半分不正解というような結果となりました.Loss関数のbackward計算の実装方法の差異による学習時間への影響は些細なもののようです.学習時間へ支配的な影響を与えているのは,ネットワークの各層を計算するために要するConvolutionなどの実装方法のようです.分かってしまえば当たり前といえば当たり前な結論ですね.
ただし,今回の実験ではPyTorchの0.1.10を使いましたが,執筆時点の最新版である0.1.12でも実験をしてみたところ,むしろChainerの方が早いという結果になりました.PyTorchはまさしく開発中なんだなという印象です.コードはgithubにあるので,開発が落ち着いたころに再度実験してみようと思います.