この記事について
この記事は、CourseraのMachine Learningのビデオ講義+宿題についてまとめたものです。
今週はWeek5(ニューラルネットワークの学習)についてです。
Week4(ニューラルネットワークの表現について)のQiita記事はこちら
Week5で学習すること
- ニューラルネットワークのパラメータの学習のためのバックプロパゲーションについて
- Θの初期化について
- Jの偏微分の正当性を確認するために必要な、微分チェックについて
コスト関数とバックプロパゲーション
記法の説明
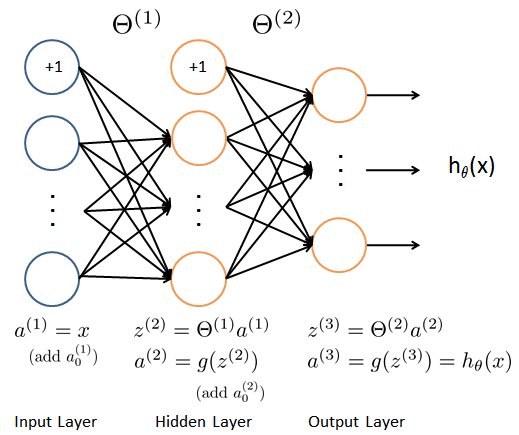
先週の講義より、ニューラルネットワークは以下のようなモデルで表されると習った。
ここで、以下のように定義しておく。
L:モデルのレイヤの数\\
s_{l}:l層におけるユニット数
ニューラルネットワークのコスト関数
今週はモデルの学習なので、まずはいつものようにコスト関数を定義する。活性化関数にシグモイド関数を使った場合のニューラルネットワークのコスト関数は、ロジスティック回帰で使ったコスト関数を、より一般化したものである。
ロジスティック回帰のコスト関数は以下の通りである。
J(\theta) = -\frac{1}{m}\Biggl[\sum_{i=1}^{m}y^{(i)}\log(h_\theta(x^{(i)})) + (1-y^{(i)})\log(h_\theta(x^{(i)}))\Biggr] + \frac{\lambda}{2m}\sum_{j=1}^{n}(\theta_{j})^2
ただし、
y \in \unicode{x211D},\quad h_\theta(x) \in \unicode{x211D}
活性化関数にシグモイド関数を使った場合の、ニューラルネットワークのコスト関数では、以下のようになる。ソフトマックス関数など、別の活性化関数を使う場合はこれとは別のコスト関数になるため注意が必要である。
J(\Theta) = -\frac{1}{m}\Biggl[\sum_{i=1}^{m}\sum_{k=1}^{K}y^{(i)}_k\log(h_\Theta(x^{(i)}))_k + (1-y^{(i)}_k)\log(h_\Theta(x^{(i)}))_k\Biggr] + \frac{\lambda}{2m}\sum_{l=1}^{L-1} \sum_{i=1}^{s_l}\sum_{j=1}^{s_l+1}(\Theta^{(l)}_{ji})^2
ただし、
y_k \in \unicode{x211D}^K,\quad h_\Theta(x) \in \unicode{x211D}^K,\quad(h_\Theta(x))_k = k^{th} output\\
上記のニューラルネットワークのコスト関数について、まず右辺第1項では、K個の出力ユニットがあるため、その和を計算している。また、K個の出力ユニットそれぞれを区別するために、kという添え字を使ってyとhを表現している。
第2項は正則化のための項で、各レイヤのΘの各要素の2乗和を取るということである。ただし、バイアス項に対応する値は除くため、iは1から始める。(ただしバイアス項を足したとしても、大体うまくいく。)
コスト関数の最小化
次に、先ほどのニューラルネットワークのコスト関数を最小化することを考える。これは以下のように、各レイヤのΘの各要素でJを偏微分したものとして表される。
\frac{\partial}{\partial \Theta^{(l)}_{ij}}J(\Theta), \quad \Theta^{(l)}_{ij} \in \unicode{x211D}
これは、Θを微小変化させた時に、コストJの変化を見ていることになる。この偏微分を実行するために、バックプロパゲーション(誤差逆伝搬法)という手法を用いる。
バックプロパゲーションとは
出力と正解値との誤差を、出力層から入力層に向かって各層で誤差を伝播してゆきながら、その誤差が小さくなるようにΘを修正してゆく手法をバックプロパゲーション(誤差逆伝搬法)という。
バックプロパゲーションアルゴリズム
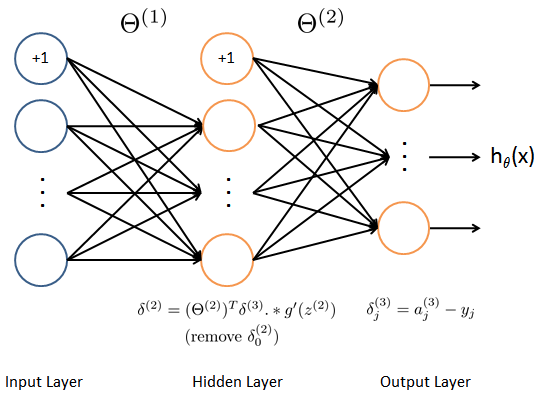
上図のようなレイヤ数3の場合のバックプロパゲーションアルゴリズムは以下のようになる(正確には手順2からがバックプロパゲーションといわれるものである)。
手順1〜4までは各トレーニングデータを一つずつ取り出して、そのデータに対して処理を行う、ということをすべてのトレーニングデータに対して行う(for文を使うのがおススメ)。その後、手順5を行う。
- 準備
各レイヤのΘを初期化する。初期化ではΘの各要素はすべて0にするとニューラルネットワークが失敗してしまう。そこで、あらかじめ決められた小さな値εで幅をもたせてその中でランダムに値をΘに割り振る。
-\epsilon \leq \Theta^{(l)}_{ij} \leq \epsilon
- 手順1
まず、フィードフォワードプロセスを実行する。具体的には、入力層から出力層に向かって各レイヤにおけるz,aを求める。具体的には、以下のように計算する。
a^{(1)} = x\hspace{30pt}\\
z^{(2)} = \Theta^{(1)}a^{(1)}\\
\hspace{34pt} a^{(2)} = g(z^{(2)})\;\;(add\;a^{(2)}_0)\\
z^{(3)} = \Theta^{(2)}a^{(2)}\\
\hspace{26pt} a^{(3)} = h_\Theta(x) = g(z^{(3)})\\
- 手順2
ここから、バックプロパゲーションが始まる。まず、出力層における、誤差を計算する
\delta^{(3)}_k = (a^{(3)}_k − y_k)
- 手順3
次に、レイヤ2(隠れ層)における誤差を次式で計算する。
\delta^{(2)} = (\Theta^{(2)})^T \delta^{(3)}.*g'(z^{(2)})
ここで、例えばg(z)がシグモイド関数なら、その微分g'(z)は次式のように表せる。
g'(z) = \frac{d}{dz}g(z) = g(z)(1-g(z))
- 手順4
各トレーニングデータでレイヤ毎に計算した誤差を蓄積するために、レイヤ毎に誤差を格納する行列Δを用意し、そこに誤差を加える。
\Delta^{(l)} = \Delta^{(l)} + \delta^{(l+1)}(a^{(l)})^T
- 手順5
すべてのトレーニングデータについて手順1〜4を実行したあと、レイヤ毎に蓄積された誤差Δをトレーニングデータ数で割ったものが、JのΘにおける偏微分となる。オーバーフィッティングを防ぐために、j≧1の場合は正規化項を足している。
\frac{\partial}{\partial \Theta^{(l)}_{ij}}J(\Theta) = D^{(l)}_{ij} =\frac{1}{m}\Delta^{(l)}_{ij} \hspace{60pt} for\;j=0
\frac{\partial}{\partial \Theta^{(l)}_{ij}}J(\Theta) = D^{(l)}_{ij} =\frac{1}{m}\Delta^{(l)}_{ij} + \frac{\lambda}{m}\Theta^{(l)}_{ij} \qquad for\;j\geq1
微分チェック
バックプロパゲーション(特にJのΘによる偏微分)は実装が複雑なため、パッと見はうまくいっているように見えるが実はバグが含まれれていることがあり、見つけることが難しい。
自分が実装したバックプロパゲーションアルゴリズムのJの偏微分が正しく動作しているかチェックするために、微分チェックといわれる方法で確認する。これは、$\epsilon$が十分小さいとき、以下の式が成立することを利用する。
\frac{\partial}{\partial \theta_1}J(x)\approx\frac{J(\theta_1+\epsilon,\theta_2,\theta_3,...,\theta_n) - J(\theta_1-\epsilon,\theta_2,\theta_3,...,\theta_n)}{2\epsilon}\\
\frac{\partial}{\partial \theta_2}J(x)\approx\frac{J(\theta_1,\theta_2+\epsilon,\theta_3,...,\theta_n) - J(\theta_1,\theta_2-\epsilon,\theta_3,...,\theta_n)}{2\epsilon}\\
\vdots\\
\frac{\partial}{\partial \theta_n}J(x)\approx\frac{J(\theta_1,\theta_2,\theta_3,...,\theta_n+\epsilon) - J(\theta_1,\theta_2,\theta_3,...,\theta_n-\epsilon)}{2\epsilon}
この値と、バックプロパゲーションで算出したJの偏微分の値が十分に近かったら、自分で実装したものが正しいと確信できる。
ニューラルネットワークの学習のまとめ
1.各レイヤのΘをランダムな値で初期化する(準備)
2.すべてのトレーニングデータを使って、フィードフォワードプロパゲーションにより、hを求める(上の手順1)
3.hにより、コスト関数Jを求める
4.すべてのトレーニングデータを使って、バックプロパゲーションにより、JのΘによる偏微分を求める(上の手順2~5)
5.微分チェックにより、Jの偏微分の正当性を確認する(問題がなければ、微分チェックはコメントアウトしておく)
7.Jと、JのΘによる偏微分を使って最適化処理にかけることで、パラメータΘを求める
宿題の実装コード
宿題の実装コードはここにあります。
https://github.com/ykoga-kyutech/CourseraMachineLearning/tree/master/ex4
実装のほとんどは、上の式をそのまま実装したものですので、数式と対応するコードを見比べながら読むと良いでしょう。