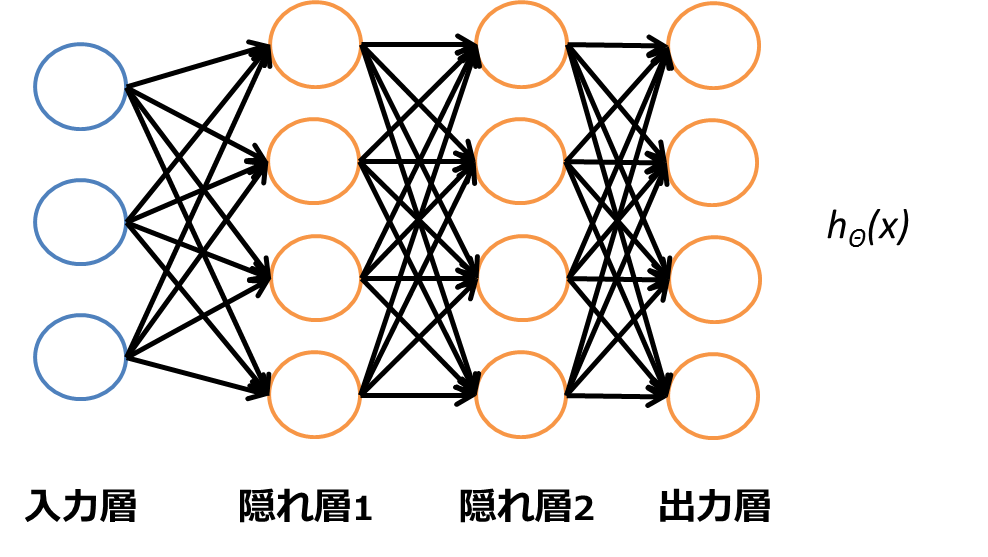week4で学習すること
- ニューラルネットワークのモデル化
- ニューラルネットワークによる多クラス分類
ニューラルネットワーク
ニューラルネットワークとは?
脳を模倣しようとしたデータ構造とアルゴリズム。
ニューラルネットワークは脳のニューロンのネットワークをシミュレーションすることで発展した。
そこで、まずはニューロンについて説明を行う。
ニューロンのモデル化
ニューロンは、たくさんの入力を受け取り、なんらかの計算を行い、その出力を別のニューロンに送る計算ユニット。以下の図のようにモデル化できる。

ここでは、ニューロンをロジスティック回帰としてモデル化している。$h_\theta(x)$は以下のとおり。
h_\theta(x) = \frac{1}{1 + e^{-\theta^T x}}
ここで$\theta$と$x$は以下のとおり。
\theta = \begin{pmatrix}
\theta_0\\
\theta_1\\
\theta_2\\
\theta_3
\end{pmatrix}
,
\hspace{10px}
x = \begin{pmatrix}
x_0\\
x_1\\
x_2\\
x_3
\end{pmatrix}
$x_0$はバイアス項で常に$x_0=1$。そのため$x_0$は図には書かないことがある。
また、$\theta$はパラメータベクトルで、重みと呼ばれることもある。ここで$\theta_0$はバイアス項にかかる重みを表す。
ニューラルネットワークのモデル化
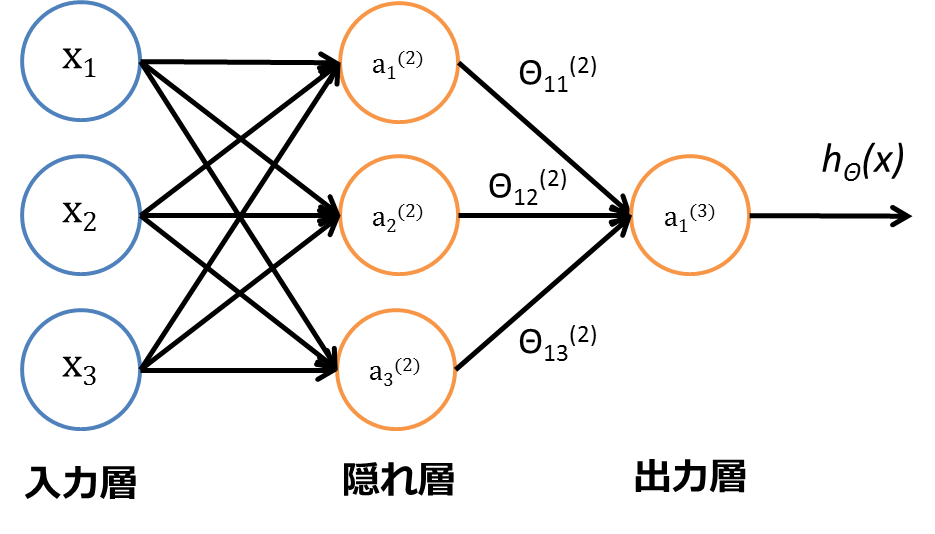
ニューラルネットワークは、ニューロンがいくつか集まったグループのこと。以下の図のように表すことができる。
記法の説明
a_i^{(j)} = j層のi番目のユニットの出力\\
\Theta^{(j)} = j層からj+1層への重みを表す行列
$j$層に$s_j$個のユニット、$j+1$層に$s_{j+1}$個のユニットがあるとき、$\Theta^{(j)}$の次元は$s_{j+1} \times (s_j+1)$となる。
これらを用いて、出力$h_\Theta(x)$は以下のように計算できる。
a_1^{(2)} = g(\Theta_{10}^{(1)}x_0 + \Theta_{11}^{(1)}x_1 + \Theta_{12}^{(1)}x_2 + \Theta_{13}^{(1)}x_3)\\
a_2^{(2)} = g(\Theta_{20}^{(1)}x_0 + \Theta_{21}^{(1)}x_1 + \Theta_{22}^{(1)}x_2 + \Theta_{23}^{(1)}x_3)\\
a_3^{(2)} = g(\Theta_{30}^{(1)}x_0 + \Theta_{31}^{(1)}x_1 + \Theta_{32}^{(1)}x_2 + \Theta_{33}^{(1)}x_3)\\
h_{\Theta}(x) = a_1^{(3)} = g(\Theta_{10}^{(2)}a_0^{(2)} + \Theta_{11}^{(2)}a_1^{(2)} + \Theta_{12}^{(2)}a_2^{(2)} + \Theta_{13}^{(2)}a_3^{(2)})
ここで$g$はロジスティック関数とする。
多クラス分類
以下の図のように、出力層のユニットを複数用意することで、多クラス分類も行える。
このとき出力を以下のようにベクトルの一要素だけ1になるようにする。
h_\Theta(x) \approx \begin{pmatrix}
1\\
0\\
0\\
0
\end{pmatrix}
,
\hspace{10px}
h_\Theta(x) \approx \begin{pmatrix}
0\\
1\\
0\\
0
\end{pmatrix}
,
\hspace{10px}
h_\Theta(x) \approx \begin{pmatrix}
0\\
0\\
1\\
0
\end{pmatrix}
,
\hspace{10px}
\hspace{10px}
h_\Theta(x) \approx \begin{pmatrix}
0\\
0\\
0\\
1
\end{pmatrix}
手書き数字認識のようなタスクを考えた時に、
h_\Theta(x) \approx \begin{pmatrix}
1\\
0\\
0\\
0
\end{pmatrix}
の場合は「数字の0」のように各ベクトルに対してラベルを割り当てることで、多クラス分類を行うことができる。
手書き数字分類
以下の図のような0~9までの手書き数字をロジスティック回帰とニューラルネットワークを用いて分類する場合を考える。

今回、分類に使うニューラルネットワークは入力層、隠れ層、出力層それぞれ一つずつの3層から構成されている。
入力層には20px$\times$20pxの画像をベクトル化した400個の数値が入力される。バイアス項が存在するので、入力層のユニット数は401となる。出力層のユニット数は0〜9までの数字を認識するために10個ある。また、隠れ層のユニット数はバイアス項を含めて26個である。
ロジスティック回帰を用いた場合の精度は94.6%であったのに対し、ニューラルネットワークを用いた場合は97.5%であった。
ソースコード
演習のコードをPythonで書いたので、読みたい人はどうぞ。
参考資料
- Coursera week4 NEURAL NETWORKS: REPRESENTATION
- ロジスティック回帰
- scipy.optimize.fmin_cgのドキュメント