13分でわかるロジスティック回帰

本記事では、こちらのサイト を参考にロジスティック回帰(Logistic regression)による分類問題の解き方を説明します。

#ロジスティック回帰
##ロジスティック回帰とは（２値分類版）
入力 $x \in \mathbb{R}^n$ を二つのクラスに分類する問題は、入力 $x$ を出力 $y \in \{0,1\}$ に割り当てる問題だととらえることが出来ます。ロジスティック回帰では 入力が$x$のときに出力が $y=1$ となる確率 $p(y=1\ |\ x; \theta)$ を次のように定義します。

p(y=1\ |\ x; \theta) := \frac{1}{1+\mathrm{e}^{-\theta \cdot \tilde{x}}}\\
ただし、\theta \in \mathbb{R}^{n+1},\  \tilde{x} :=  \left(\begin{array}{cc}1\\ x\end{array}\right)

$y=0$ となる確率は、 $p(y=0\ |\ x; \theta) = 1- p(y=1\ |\ x; \theta)$ で得ることができます。
この確率を用いて、トレーニングセット $(x_i, y_i),\ 1 \leq i \leq m$ に関するコスト関数(Cost function)¹

\mathrm{Cos} (\theta) := -\frac{1}{m} \sum_{i=1}^m \log \left( p(y=y_i\ |\ x_i; \theta)\right)

を最小化する $\theta_{min}$ を求めます。この $\theta_{min}$ を用いて本当の確率は $p(y=1\ |\ x; \theta_{min})$ だと考えるのがロジスティック回帰です。

###参考
上の $\theta_{min}$ は尤度(Likelihood)と呼ばれる確率の積

L(\theta) := \prod_{i=1}^m p(y=y_i\ |\ x_i; \theta)

を最大にする $\theta_{LM}$ と等しいです。なぜなら $\mathrm{Cos} (\theta) = -(1/m)\log L(\theta)$ であり、$\log x \ (x > 0)$ は単調増加なので引数の大小関係を変えないからです。このトレーニングセットが起こる確率を最大にする考え方を最尤推定法(Maximum likelihood estimation)と呼びます。

##シグモイド関数による２値分類
上の $p(y=1\ |\ x; \theta)$ の右辺に現れた関数

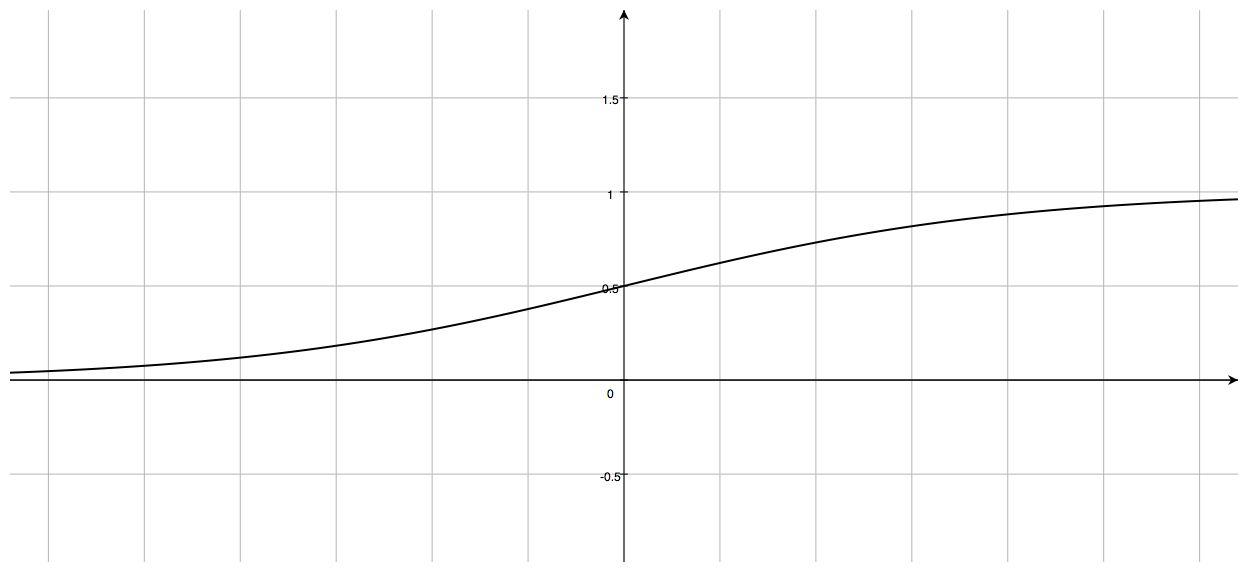
g(z) = \frac{1}{1+\mathrm{e}^{-z}}

をシグモイド関数(Sigmoid function)といいます。

シグモイド関数は次のような性質を持っています。

1. $0 < g(z) < 1\ (\lim_{z\to -\infty}g(z) = 0,\ \lim_{z\to \infty}g(z) = 1)$
2. $g(0) = 0.5$
3. $(x, y) = (0, 0.5)$ を中心として点対称
4. 微分可能

1.によってシグモイド関数を確率と見なすことができますし、確率ではなくて二つのクラスに分類した結果が欲しいときは以下のように使います。

\left \{
\begin{array}{ll}
y=1 & (g(z)\geq 0.5 \ つまり、z\geq 0)\\
y=0 & (g(z) < 0.5 \ つまり、z < 0)
\end{array}
\right .

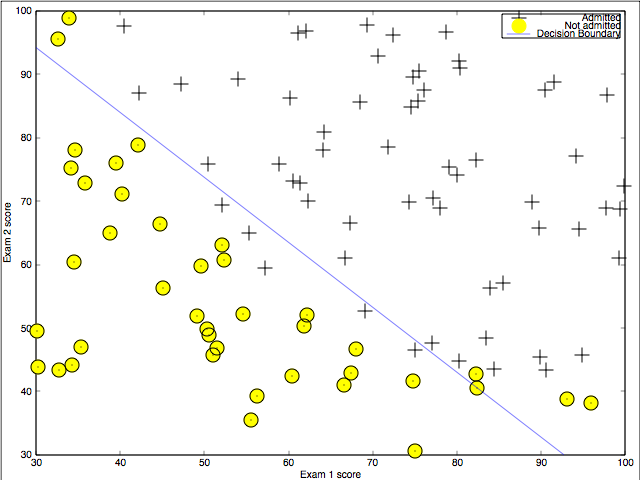
上の分類法から $z=0$ が分類の境界になっていることがわかります。この境界がロジスティック回帰による決定境界(Dicision boundary)です。

###参考
シグモイド関数 $g$ の逆関数は

z= \log \frac{g}{1-g}

と与えられます。これを私たちの $p(y=1\ |\ x; \theta)$ に適用すると

\theta \cdot \tilde{x}　= \log \frac{p(y=1\ |\ x; \theta)}{1-p(y=1\ |\ x; \theta)}

を得ます。ある事象が起こる確率 $p$ と起こらない確率 $1-p$ の比 $p/(1-p)$ はオッズ比と呼ばれます。つまり、確率としてシグモイド関数を用いることは、オッズ比の対数が入力の線形和で表されると仮定していることになります。

##最急降下法によるパラメータの決定
上記２節をまとめると、 ロジスティック回帰の決定境界は $\theta \cdot \tilde{x} = 0$ であり、決定境界を求める為には $\theta$ が必要になります。実際、$\mathrm{Cos}(\theta)$ を最小にする最急降下法(ラーニングレート $\alpha$ で $k(\geq 1)$ ステップ)によって次のように求まります。

\begin{eqnarray}
\theta^{(k)} &=& \theta^{(k-1)} - \alpha\cdot \mathrm{grad} \ \mathrm{Cos}(\theta^{(k-1)})\\
&=&\theta^{(k-1)} - \alpha\cdot \sum_{i=1}^m \left \{ \frac{1}{1+\mathrm{e}^{-\theta^{(k-1)}\cdot \tilde{x_i}}} - y_i \right \}\tilde{x_i}
\end{eqnarray}

ここで、 $\tilde{x_i} = (1, x_i)^{\mathrm{T}}$ であり、 $\theta^{(0)}$ は初期値として与えるものです。

最急降下法以外にも以下の３つのアルゴリズムが名称だけ紹介されています。

• 共役勾配法(Conjugate gradient)
• BFGS
• L-BFGS

上記３つのアルゴリズムを最急降下法と比べると、次のメリット・デメリットがあります。
メリット
・ ラーニングレートが必要ない
・ 最急降下法に比べて速いことが多い

デメリット
・ 複雑

##多値分類問題への応用

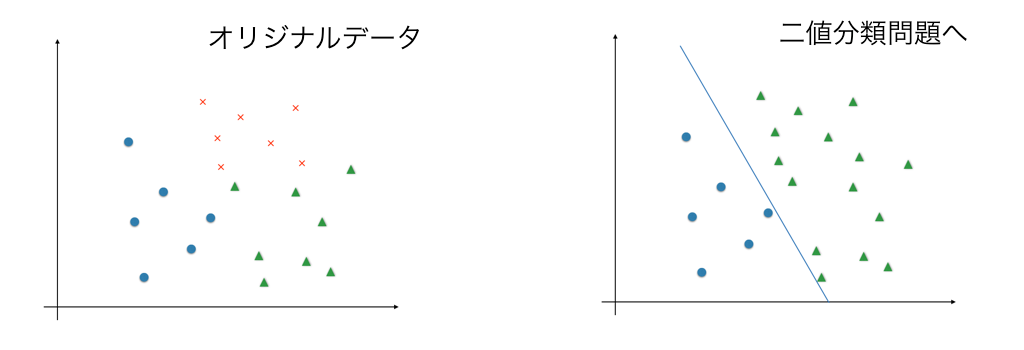
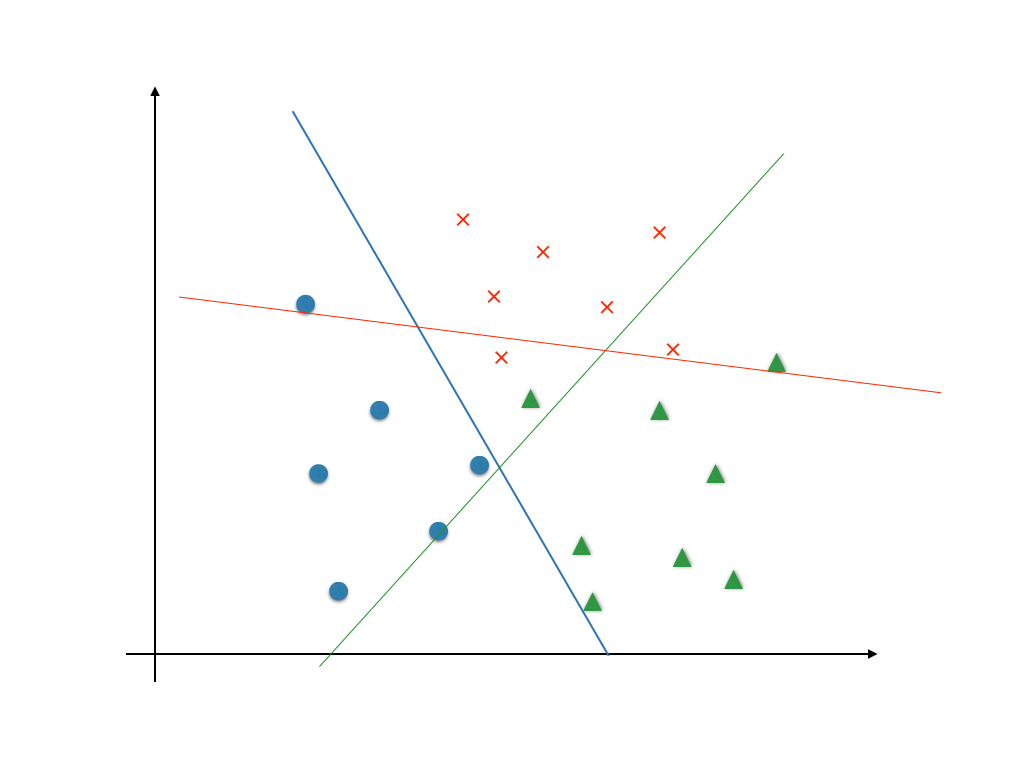
nクラス分類問題は、入力 $x$ を出力 $y \in \{1, \cdots , n \}$ に割り当てる問題だととらえることが出来ます。ロジスティック回帰においては、次のように解きます。

１.　$i \in \{ 1, \cdots , n \}$ に対して $y=i$ と $y \neq i$ の２値分類問題を考え $\theta^{(i)}_{min}$を求める。
（上付き添字(i)は最急勾配法のときのそれとは意味が違うことに注意）

つまり、 $y=i$ である確率を

p \left( y=i\ \left| \right. \ x; \theta_{min}^{(i)} \right) :=  \frac{1}{1+\mathrm{e}^{-\theta_{min}^{(i)} \cdot \tilde{x}}}

と考える。

２.　入力 $x$ を 確率　$p \left( y=i\ \left| \right. \ x; \theta_{min}^{(i)} \right)$ が一番大きい $i$ クラスであると判定する。

#□参考文献

機械学習のための確率と統計（講談社）
http://www.amazon.co.jp/機械学習のための確率と統計-機械学習プロフェッショナルシリーズ-杉山-将/dp/4061529013

確率的最適化（講談社）
http://www.amazon.co.jp/確率的最適化-機械学習プロフェッショナルシリーズ-鈴木-大慈/dp/4061529072

1. 損失関数(Loss function)とも呼ばれます。 ↩