西洋将棋 chess の女王 Queen は、将棋の飛車・角の働きを併せ持ちます。すなわち、自身の場所を基準にして、縦・横・斜めの駒に効きます。$N \times N$ の碁盤に、$N$ 個の Queen を互いに効かないように配置する問題を、N-Queen 問題といいます。
Julia の数理最適化パッケージ JuMP を用いて、N-Queen問題を解いてみましょう。JuMP に関しては、拙文 Qitta記事 「最適化におけるJulia - JuMP事始め」 で紹介しました。
対話的に解いてみる
まずコマンドライン (REPL) から対話的に解いてみましょう。
JuMP パッケージを導入して、モデル m を作ります。
julia> using JuMP
julia> using Cbc
julia> m = Model( solver=CbcSolver() )
Feasibility problem with:
* 0 linear constraints
* 0 variables
Solver is default solver
■ 2017/05/23 修正---
solverを 2017年1月当時の元記事の ClpSolver から CbcSolver に変更しました。
■ 修正終わり ----
変数
実際の西洋将棋と同じように、$n=8$ とします。$n \times n$ の碁盤に見立てた2次元配列 $a$ を、変数として作成します。$a[i,j]$ はバイナリ型とします。すなわち、$a[i,j]$ の値は、$1$ (その位置に Queenが存在)または $0$ (存在しない)のどちらかです。
julia> n = 8
8
julia> @variable(m, a[1:n,1:n], Bin)
8×8 Array{JuMP.Variable,2}:
a[1,1] a[1,2] a[1,3] a[1,4] a[1,5] a[1,6] a[1,7] a[1,8]
a[2,1] a[2,2] a[2,3] a[2,4] a[2,5] a[2,6] a[2,7] a[2,8]
a[3,1] a[3,2] a[3,3] a[3,4] a[3,5] a[3,6] a[3,7] a[3,8]
a[4,1] a[4,2] a[4,3] a[4,4] a[4,5] a[4,6] a[4,7] a[4,8]
a[5,1] a[5,2] a[5,3] a[5,4] a[5,5] a[5,6] a[5,7] a[5,8]
a[6,1] a[6,2] a[6,3] a[6,4] a[6,5] a[6,6] a[6,7] a[6,8]
a[7,1] a[7,2] a[7,3] a[7,4] a[7,5] a[7,6] a[7,7] a[7,8]
a[8,1] a[8,2] a[8,3] a[8,4] a[8,5] a[8,6] a[8,7] a[8,8]
変数 a が、碁盤の目のように表示されました。Julia の行列要素 $a[i,j]$ は、数学の教科書と同じように配置されます。「行→ 列↓」
参考→ Qiita記事 「【プログラマーのための数学】行列」
制約条件
制約条件を設定していきます。
数理モデルは、Qiita記事 「組合せ最適化でN Queen問題を解く」 を参考にします。
制約条件(1)
【各行について、列に沿った総和が $1$ となる】
@constraint マクロで、制約条件を書きます。複数の制約条件を同時に設定できます。
制約式で、総和をとるのに sum() 関数を使います。その () 内では comprehension を使うことができます。
julia> @constraint(m, [i=1:n], sum(a[i,j] for j=1:n) == 1)
8-element Array{JuMP.ConstraintRef,1}:
a[1,1] + a[1,2] + a[1,3] + a[1,4] + a[1,5] + a[1,6] + a[1,7] + a[1,8] = 1
a[2,1] + a[2,2] + a[2,3] + a[2,4] + a[2,5] + a[2,6] + a[2,7] + a[2,8] = 1
a[3,1] + a[3,2] + a[3,3] + a[3,4] + a[3,5] + a[3,6] + a[3,7] + a[3,8] = 1
a[4,1] + a[4,2] + a[4,3] + a[4,4] + a[4,5] + a[4,6] + a[4,7] + a[4,8] = 1
a[5,1] + a[5,2] + a[5,3] + a[5,4] + a[5,5] + a[5,6] + a[5,7] + a[5,8] = 1
a[6,1] + a[6,2] + a[6,3] + a[6,4] + a[6,5] + a[6,6] + a[6,7] + a[6,8] = 1
a[7,1] + a[7,2] + a[7,3] + a[7,4] + a[7,5] + a[7,6] + a[7,7] + a[7,8] = 1
a[8,1] + a[8,2] + a[8,3] + a[8,4] + a[8,5] + a[8,6] + a[8,7] + a[8,8] = 1
制約条件が数式で表示されました。確認に便利ですね。
制約条件が複雑な場合には、@expression 文で、式に名前を付けてから、その式を用いて制約条件を書くこともできます。例えば、この場合なら、以下のように二段構えにします。(Julia では識別子に漢字を使えます。)
julia> @expression(m, 列の和[i=1:n], sum(a[i,j] for j=1:8))
8-element Array{JuMP.GenericAffExpr{Float64,JuMP.Variable},1}:
a[1,1] + a[1,2] + a[1,3] + a[1,4] + a[1,5] + a[1,6] + a[1,7] + a[1,8]
a[2,1] + a[2,2] + a[2,3] + a[2,4] + a[2,5] + a[2,6] + a[2,7] + a[2,8]
a[3,1] + a[3,2] + a[3,3] + a[3,4] + a[3,5] + a[3,6] + a[3,7] + a[3,8]
a[4,1] + a[4,2] + a[4,3] + a[4,4] + a[4,5] + a[4,6] + a[4,7] + a[4,8]
a[5,1] + a[5,2] + a[5,3] + a[5,4] + a[5,5] + a[5,6] + a[5,7] + a[5,8]
a[6,1] + a[6,2] + a[6,3] + a[6,4] + a[6,5] + a[6,6] + a[6,7] + a[6,8]
a[7,1] + a[7,2] + a[7,3] + a[7,4] + a[7,5] + a[7,6] + a[7,7] + a[7,8]
a[8,1] + a[8,2] + a[8,3] + a[8,4] + a[8,5] + a[8,6] + a[8,7] + a[8,8]
julia> @constraint(m, [i=1:n], 列の和[i] == 1)
8-element Array{JuMP.ConstraintRef,1}:
a[1,1] + a[1,2] + a[1,3] + a[1,4] + a[1,5] + a[1,6] + a[1,7] + a[1,8] = 1
a[2,1] + a[2,2] + a[2,3] + a[2,4] + a[2,5] + a[2,6] + a[2,7] + a[2,8] = 1
a[3,1] + a[3,2] + a[3,3] + a[3,4] + a[3,5] + a[3,6] + a[3,7] + a[3,8] = 1
a[4,1] + a[4,2] + a[4,3] + a[4,4] + a[4,5] + a[4,6] + a[4,7] + a[4,8] = 1
a[5,1] + a[5,2] + a[5,3] + a[5,4] + a[5,5] + a[5,6] + a[5,7] + a[5,8] = 1
a[6,1] + a[6,2] + a[6,3] + a[6,4] + a[6,5] + a[6,6] + a[6,7] + a[6,8] = 1
a[7,1] + a[7,2] + a[7,3] + a[7,4] + a[7,5] + a[7,6] + a[7,7] + a[7,8] = 1
a[8,1] + a[8,2] + a[8,3] + a[8,4] + a[8,5] + a[8,6] + a[8,7] + a[8,8] = 1
制約条件(2)
【各行について、列に沿った総和が $1$ となる】
(1)と同様ですね。
julia> @constraint(m, [j=1:n], sum(a[i,j] for i=1:n) == 1)
8-element Array{JuMP.ConstraintRef,1}:
a[1,1] + a[2,1] + a[3,1] + a[4,1] + a[5,1] + a[6,1] + a[7,1] + a[8,1] = 1
a[1,2] + a[2,2] + a[3,2] + a[4,2] + a[5,2] + a[6,2] + a[7,2] + a[8,2] = 1
a[1,3] + a[2,3] + a[3,3] + a[4,3] + a[5,3] + a[6,3] + a[7,3] + a[8,3] = 1
a[1,4] + a[2,4] + a[3,4] + a[4,4] + a[5,4] + a[6,4] + a[7,4] + a[8,4] = 1
a[1,5] + a[2,5] + a[3,5] + a[4,5] + a[5,5] + a[6,5] + a[7,5] + a[8,5] = 1
a[1,6] + a[2,6] + a[3,6] + a[4,6] + a[5,6] + a[6,6] + a[7,6] + a[8,6] = 1
a[1,7] + a[2,7] + a[3,7] + a[4,7] + a[5,7] + a[6,7] + a[7,7] + a[8,7] = 1
a[1,8] + a[2,8] + a[3,8] + a[4,8] + a[5,8] + a[6,8] + a[7,8] + a[8,8] = 1
制約条件(3)
【 $i + j = (一定)$ に沿った総和が 1以下】
上の碁盤を眺めながら、$(i+j)$ の一定値を求めました。
sum() の comprehension の中で、if で条件式を追加できます。
julia> @constraint(m, [k=3:2*n-1], sum(a[i,j] for i=1:n,j=1:n if i+j==k ) <= 1)
JuMP.JuMPArray{JuMP.ConstraintRef,1,Tuple{UnitRange{Int64}}}(JuMP.ConstraintRef[a[1,2] + a[2,1] ≤ 1,a[1,3] + a[2,2] + a[3,1] ≤ 1,a[1,4] + a[2,3] + a[3,2] + a[4,1] ≤ 1,a[1,5] + a[2,4] + a[3,3] + a[4,2] + a[5,1] ≤ 1,a[1,6] + a[2,5] + a[3,4] + a[4,3] + a[5,2] + a[6,1] ≤ 1,a[1,7] + a[2,6] + a[3,5] + a[4,4] + a[5,3] + a[6,2] + a[7,1] ≤ 1,a[1,8] + a[2,7] + a[3,6] + a[4,5] + a[5,4] + a[6,3] + a[7,2] + a[8,1] ≤ 1,a[2,8] + a[3,7] + a[4,6] + a[5,5] + a[6,4] + a[7,3] + a[8,2] ≤ 1,a[3,8] + a[4,7] + a[5,6] + a[6,5] + a[7,4] + a[8,3] ≤ 1,a[4,8] + a[5,7] + a[6,6] + a[7,5] + a[8,4] ≤ 1,a[5,8] + a[6,7] + a[7,6] + a[8,5] ≤ 1,a[6,8] + a[7,7] + a[8,6] ≤ 1,a[7,8] + a[8,7] ≤ 1],(3:15,),(Dict{Int64,Int64}(),),Dict{Symbol,Any}())
結果に、数式が入っていますが、ごちゃごちゃしていますね。制約条件の添字をずらして 1 から始めるようにすれば、制約 (1),(2)のように、数式だけ表示されます。式中で「 $≤$ 」が使えるのもかっこよいです。
julia> @constraint(m, [k=1:2*n-3], sum(a[i,j] for i=1:n,j=1:n if i+j==k+2 ) <= 1)
13-element Array{JuMP.ConstraintRef,1}:
a[1,2] + a[2,1] ≤ 1
a[1,3] + a[2,2] + a[3,1] ≤ 1
a[1,4] + a[2,3] + a[3,2] + a[4,1] ≤ 1
a[1,5] + a[2,4] + a[3,3] + a[4,2] + a[5,1] ≤ 1
a[1,6] + a[2,5] + a[3,4] + a[4,3] + a[5,2] + a[6,1] ≤ 1
a[1,7] + a[2,6] + a[3,5] + a[4,4] + a[5,3] + a[6,2] + a[7,1] ≤ 1
a[1,8] + a[2,7] + a[3,6] + a[4,5] + a[5,4] + a[6,3] + a[7,2] + a[8,1] ≤ 1
a[2,8] + a[3,7] + a[4,6] + a[5,5] + a[6,4] + a[7,3] + a[8,2] ≤ 1
a[3,8] + a[4,7] + a[5,6] + a[6,5] + a[7,4] + a[8,3] ≤ 1
a[4,8] + a[5,7] + a[6,6] + a[7,5] + a[8,4] ≤ 1
a[5,8] + a[6,7] + a[7,6] + a[8,5] ≤ 1
a[6,8] + a[7,7] + a[8,6] ≤ 1
a[7,8] + a[8,7] ≤ 1
制約条件(4)
【 $i - j = (一定)$ に沿った総和が 1以下】
条件(3)と同様に、碁盤を眺めながら、$(i-j)$ の一定値を求めました。
julia> @constraint(m, [k=-n+2:n-2], sum(a[i,j] for i=1:n,j=1:n if i-j==k ) <= 1)
JuMP.JuMPArray{JuMP.ConstraintRef,1,Tuple{UnitRange{Int64}}}(JuMP.ConstraintRef[a[1,7] + a[2,8] ≤ 1,a[1,6] + a[2,7] + a[3,8] ≤ 1,a[1,5] + a[2,6] + a[3,7] + a[4,8] ≤ 1,a[1,4] + a[2,5] + a[3,6] + a[4,7] + a[5,8] ≤ 1,a[1,3] + a[2,4] + a[3,5] + a[4,6] + a[5,7] + a[6,8] ≤ 1,a[1,2] + a[2,3] + a[3,4] + a[4,5] + a[5,6] + a[6,7] + a[7,8] ≤ 1,a[1,1] + a[2,2] + a[3,3] + a[4,4] + a[5,5] + a[6,6] + a[7,7] + a[8,8] ≤ 1,a[2,1] + a[3,2] + a[4,3] + a[5,4] + a[6,5] + a[7,6] + a[8,7] ≤ 1,a[3,1] + a[4,2] + a[5,3] + a[6,4] + a[7,5] + a[8,6] ≤ 1,a[4,1] + a[5,2] + a[6,3] + a[7,4] + a[8,5] ≤ 1,a[5,1] + a[6,2] + a[7,3] + a[8,4] ≤ 1,a[6,1] + a[7,2] + a[8,3] ≤ 1,a[7,1] + a[8,2] ≤ 1],(-6:6,),(Dict{Int64,Int64}(),),Dict{Symbol,Any}())
同じく、制約条件の添字をずらして 1 から始めるようにすれば、数式だけ表示されます。
julia> @constraint(m, [k=1:2*n-3], sum(a[i,j] for i=1:n,j=1:n if i-j==k-n+1 ) <= 1)
13-element Array{JuMP.ConstraintRef,1}:
a[1,7] + a[2,8] ≤ 1
a[1,6] + a[2,7] + a[3,8] ≤ 1
a[1,5] + a[2,6] + a[3,7] + a[4,8] ≤ 1
a[1,4] + a[2,5] + a[3,6] + a[4,7] + a[5,8] ≤ 1
a[1,3] + a[2,4] + a[3,5] + a[4,6] + a[5,7] + a[6,8] ≤ 1
a[1,2] + a[2,3] + a[3,4] + a[4,5] + a[5,6] + a[6,7] + a[7,8] ≤ 1
a[1,1] + a[2,2] + a[3,3] + a[4,4] + a[5,5] + a[6,6] + a[7,7] + a[8,8] ≤ 1
a[2,1] + a[3,2] + a[4,3] + a[5,4] + a[6,5] + a[7,6] + a[8,7] ≤ 1
a[3,1] + a[4,2] + a[5,3] + a[6,4] + a[7,5] + a[8,6] ≤ 1
a[4,1] + a[5,2] + a[6,3] + a[7,4] + a[8,5] ≤ 1
a[5,1] + a[6,2] + a[7,3] + a[8,4] ≤ 1
a[6,1] + a[7,2] + a[8,3] ≤ 1
a[7,1] + a[8,2] ≤ 1
最適化を実行する
以上で、問題が記述できたので、最適化を実行します。
julia> solve(m)
:Optimal
solve は例外を発生しません。最適化できた場合には、戻り値 :Optimal が得られます。
変数の値は、関数 getvalue() で得られます。
julia> r=getvalue(a)
8×8 Array{Float64,2}:
0.0 0.0 1.0 0.0 0.0 0.0 0.0 0.0
1.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
0.0 0.0 0.0 0.0 0.0 0.0 1.0 0.0
0.0 0.0 0.0 0.0 1.0 0.0 0.0 0.0
0.0 0.0 0.0 0.0 0.0 0.0 0.0 1.0
0.0 1.0 0.0 0.0 0.0 0.0 0.0 0.0
0.0 0.0 0.0 1.0 0.0 0.0 0.0 0.0
0.0 0.0 0.0 0.0 0.0 1.0 0.0 0.0
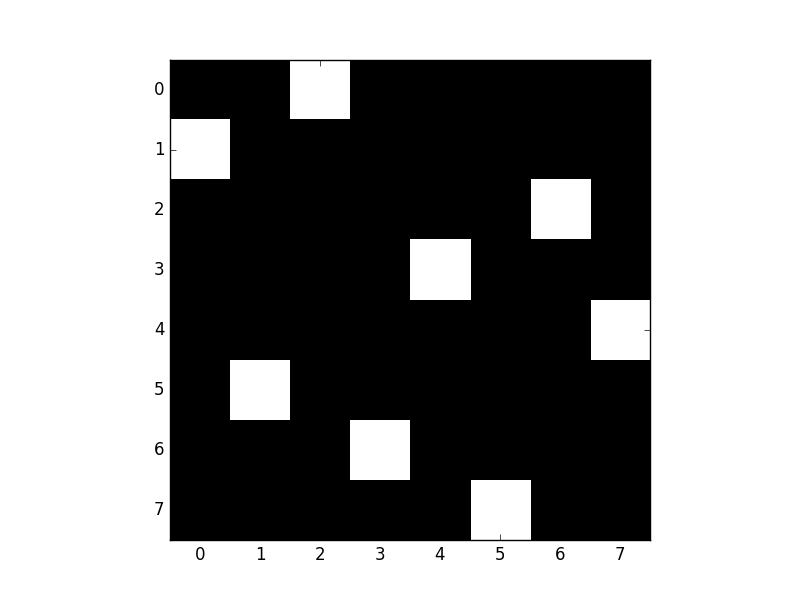
PyPlot を用いて、タイル・プロットしてみましょう。
julia> using PyPlot
julia> imshow( r, interpolation="nearest", cmap="gray")
PyObject <matplotlib.image.AxesImage object at 0x31dca8a50>
関数にまとめる
以上をまとめて、関数として呼べるようにしましょう。
using JuMP
using Cbc
function nQueen(n)
m = Model( solver=CbcSolver() )
@variable(m, a[1:n,1:n], Bin)
@constraint(m, [i=1:n], sum(a[i,j] for j=1:n) == 1)
@constraint(m, [j=1:n], sum(a[i,j] for i=1:n) == 1)
@constraint(m, [k=1:2*n-3], sum(a[i,j] for i=1:n,j=1:n if i-j==k-n+1 ) <= 1)
@constraint(m, [k=1:2*n-3], sum(a[i,j] for i=1:n,j=1:n if i+j==k+2 ) <= 1)
@time r=solve(m)
@show r
return getvalue(a)
end
using PyPlot
for n in [4,8,16,32,64,128]
r = nQueen(n)
imshow(r, interpolation="nearest", cmap="gray")
end
ある回の計算結果は、こんなでした。ご参考まで。
0.005040 seconds (97 allocations: 11.516 KB)
r = :Optimal
0.026986 seconds (5.81 k allocations: 276.491 KB)
r = :Optimal
0.033432 seconds (101 allocations: 101.203 KB)
r = :Optimal
0.184289 seconds (110 allocations: 380.281 KB)
r = :Optimal
1.290198 seconds (127 allocations: 1.456 MB)
r = :Optimal
8.779787 seconds (133 allocations: 5.790 MB)
r = :Optimal
終わりに
JuMP を使って nQueen 問題を記述・求解しました。制約条件が、数式通りに表示されて便利ですね。