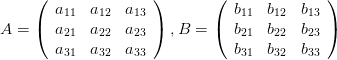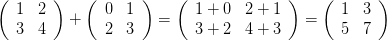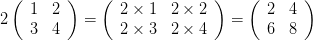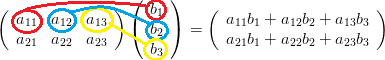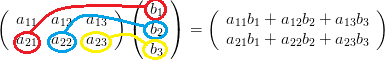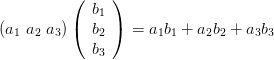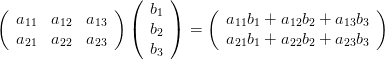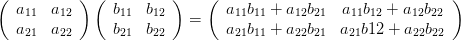目次
行=>横、列=>縦
まずは、行列で、行と列、どちらが縦か横か、下記のように覚えましょう。
行が横で、列が縦です。
行列の式の書き方
行列は上記のように書きます。
それぞれの数字のことを、成分または要素と呼びます。
上記の例でいうと、2x2の行列で、成分は4つとなります。
また、それぞれの成分の位置は、下記のような言い方で表します。
| 場所 | 名称 | 値 |
|---|---|---|
| 上段左 | (1,1)成分 | a11 |
| 上段右 | (1,2)成分 | a12 |
| 下段左 | (2,1)成分 | a21 |
| 下段右 | (2,2)成分 | a22 |
2つ行列が等しい状態にある時
また、上記のようなAとBの行列があり、A = Bという条件のとき、
同じ位置にある成分同士は等しくなります。
a11 = b11
a12 = b12
a13 = b13
a21 = b21
a22 = b22
a23 = b23
a31 = b31
a32 = b32
a33 = b33
行列の足し算、引き算
行列の加減演算は、各成分ごとに行います。
上記の例だと、下記のような結果になります。
| 場所 | 名称 | 式 | 解 |
|---|---|---|---|
| 上段左 | (1,1)成分 | 1+0 | 1 |
| 上段右 | (1,2)成分 | 2+1 | 3 |
| 下段左 | (2,1)成分 | 3+2 | 5 |
| 下段右 | (2,2)成分 | 4+3 | 7 |
引き算も同じです。
行列の和と差は、対応する成分同士での足し引きとなるため、
行数と列数の一致する行列同士でないと計算できません。
行列のスカラー倍
行列全体に対して、一つの数を掛けることができます。
| 場所 | 名称 | 式 | 解 |
|---|---|---|---|
| 上段左 | (1,1)成分 | 2x1 | 2 |
| 上段右 | (1,2)成分 | 2x2 | 4 |
| 下段左 | (2,1)成分 | 2x3 | 6 |
| 下段右 | (2,2)成分 | 2x4 | 8 |
行列の掛け算
行列の掛け算の仕方は、足し算引き算とは少し違います。
下記の図のように、左側の行と右側の列を対応させて計算します。
左(1,1)成分 x 右(1,1)成分
左(1,2)成分 x 右(2,1)成分
左(1,3)成分 x 右(3,1)成分
左(2,1)成分 x 右(1,1)成分
左(2,2)成分 x 右(2,1)成分
左(2,3)成分 x 右(3,1)成分
このような計算方法になるため、左側の「行」の要素数と、右側の「列」の要素数が同じでないと、計算できません。
下記、他の例を記載しておきます。
以上
[参考]
JSciencer - 行列
東大生が教えるビジュアル数学
[関連記事]
プログラマーのための数学 - 目次