この投稿について
線形分離可能なデータ群に対する識別境界の決定方法の1つであるパーセプトロンの学習規則をライブラリなどを使わずにPythonで実装してみました。
Python、機械学習ともに初心者なので、良くないポイントはご指摘お願いします。
「パーセプトロンの学習規則」と並んで比較される「Widrow-Hoff(ウィドロウ・ホフ)の学習規則」については「Widrow-Hoff(ウィドロウ・ホフ)の学習規則をPythonで実装」でまとめてあります。
パーセプトロンの学習規則の理論
パーセプトロンの学習規則の概要や数式については以下のスライドにざっくりとまとめてあります(スライド途中からです)。
実装
1次元の場合
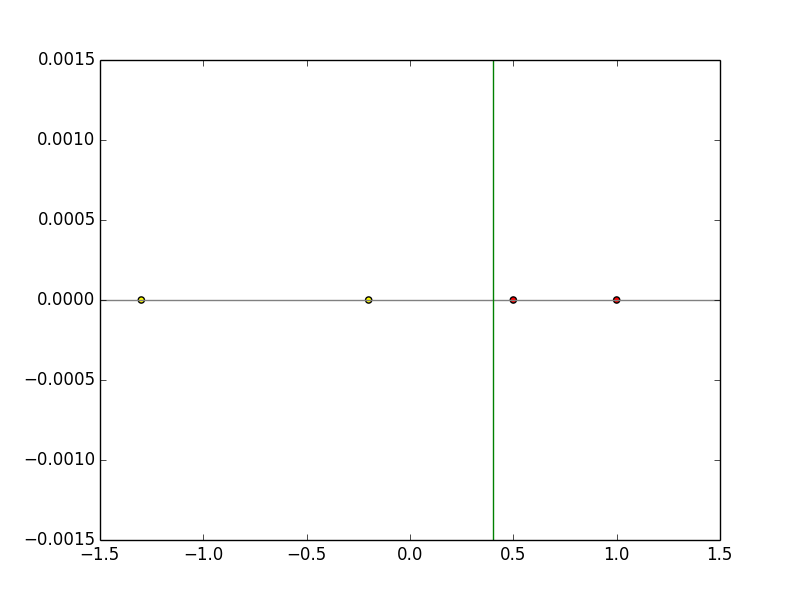
下図のような1次元上に存在し、2クラスのいずれかにに属する線形分離可能な学習データの分離境界線を求める。
実装のポイントとしては、
- 初期の重みベクトルは
w=(0.2,0.3)とし、学習係数はρ=0.5とした - 分離境界の収束判定は行わず、重みベクトルの補正(学習)は十分な回数(100回)繰り返した(本当はよくないんだろうけど、まあ機械にいっぱい仕事させるのはいいかなーと思いまして。)
実際のコードは以下のようになりました。
# coding: UTF-8
# 1次元のパーセプトロンの学習規則の実装例
import numpy as np
import matplotlib.pyplot as plt
def train(wvec, xvec, is_c1):
low = 0.5#学習係数
if (np.dot(wvec,xvec) > 0) != is_c1:
if is_c1:
wvec_new = wvec + low*xvec
else:
wvec_new = wvec - low*xvec
return wvec_new
else:
return wvec
if __name__ == '__main__':
data = np.array([[1.0, 1],[0.5, 1],[-0.2, 2],[-1.3, 2]])# データ群
features = data[:,0].reshape(data[:,0].size,1)# 特徴ベクトル
labels = data[:,1]# クラス(今回はc1=1,c2=2)
wvec = np.array([0.2, 0.3])# 初期の重みベクトル
is_c1s = (labels == 1)# c1かどうか booleanの配列
xvecs = np.c_[np.ones(features.size), features]#xvec[0] = 1
loop = 100
for j in range(loop):
for xvec, is_c1 in zip(xvecs, is_c1s):
wvec = train(wvec, xvec, is_c1)
print wvec
print -(wvec[0]/wvec[1])
# グラフ描写
plt.axhline(y=0, c='gray')
plt.scatter(features[is_c1s], np.zeros(features[is_c1s].size), c='red', marker="o")
plt.scatter(features[~is_c1s], np.zeros(features[~is_c1s].size), c='yellow', marker="o")
# 分離境界線
plt.axvline(x=-(wvec[0]/wvec[1]), c='green')
plt.show()
学習後の重みベクトルはw=(-0.3,0.75)となる。
これをwx=0の式に代入すると識別関数はx=0.4となり、下図のように学習によってうまく線形分離できていることがわかる。
2次元の場合
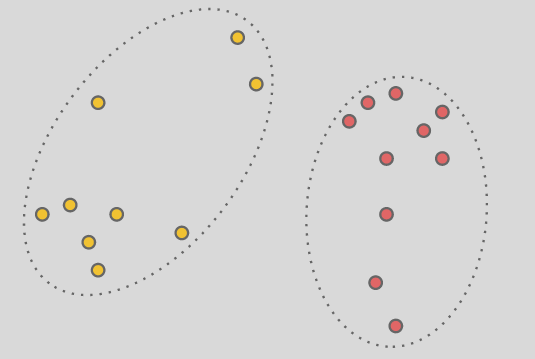
下図(イメージ)のように2次元上に存在し、2クラスのいずれかに属する線形分離可能な学習データの分離境界線を求める。
実装のポイントとしては、
-
np.random.randを用いて、線形分離可能な2クラスのデータ群を生成 - 初期の重みベクトルは
w=(2,-1,3)とし、学習係数はρ=0.5とした - 1次元の場合と同じく、分離境界の収束判定は行わず、重みベクトルの補正(学習)は十分な回数(100回)繰り返した。
実際のコードは以下のようになりました。
# coding: UTF-8
# 2次元のパーセプトロンの学習規則の実装例
import numpy as np
import matplotlib.pyplot as plt
import sys
def train(wvec, xvec, label):
low = 0.5#学習係数
if (np.dot(wvec,xvec) * label < 0):
wvec_new = wvec + label*low*xvec
return wvec_new
else:
return wvec
if __name__ == '__main__':
train_num = 100#学習データ数
#class1の学習データ
x1_1=np.random.rand(train_num/2) * 5 + 1 #x成分
x1_2=np.random.rand(int(train_num/2)) * 5 + 1 #y成分
label_x1 = np.ones(train_num/2) #ラベル(すべて1)
#class2の学習データ
x2_1=(np.random.rand(train_num/2) * 5 + 1) * -1 #x成分
x2_2=(np.random.rand(train_num/2) * 5 + 1) * -1 #y成分
label_x2 = np.ones(train_num/2) * -1 #ラベル(すべて-1)
x0=np.ones(train_num/2) # x0は常に1
x1=np.c_[x0, x1_1, x1_2]
x2=np.c_[x0, x2_1, x2_2]
xvecs=np.r_[x1, x2]
labels = np.r_[label_x1, label_x2]
wvec = np.array([2,-1,3])#初期の重みベクトル 適当に決める
loop = 100
for j in range(loop):
for xvec, label in zip(xvecs, labels):
wvec = train(wvec, xvec, label)
print wvec
plt.scatter(x1[:,1], x1[:,2], c='red', marker="o")
plt.scatter(x2[:,1], x2[:,2], c='yellow', marker="o")
#分離境界線
x_fig = np.array(range(-8,8))
y_fig = -(wvec[1]/wvec[2])*x_fig - (wvec[0]/wvec[2])
plt.plot(x_fig,y_fig)
plt.show()
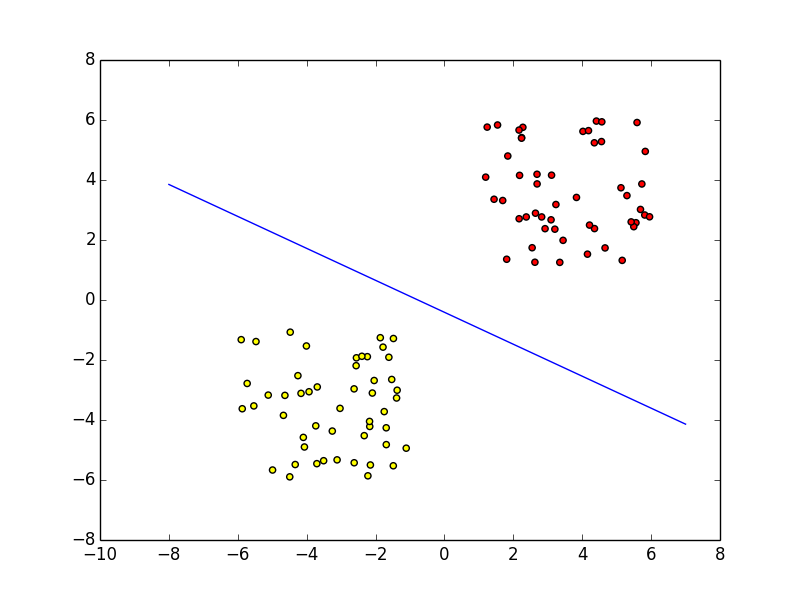
学習データをランダムで生成しているため、学習後の重みベクトルや識別関数は毎回異なるが、
実際に実行結果の一例としては下図のようになり、学習によって上手く線形分離できていることがわかる。