偶然とはなにか。コインを投げてみよう #R

偶然とはなにか

・8人の人がコインを振っても、表が4枚裏が4枚になることはない
・でもコインなら3枚表で5枚裏でもたまたま裏が多かったと思うけど、スロットで雑誌で見たテクニックで台を選んで、勝ったら、自分の力で勝ったと思ってしまう
・自分が行った施策で数字が上がれば結果が出たと思うし、結果が出なかったらでなかったと思う
=> 統計的にどのくらいの精度なのか計算できる、偶然起きるってことを体験してみよう

コインの表の出る確率を実験する

2回投げる

0が表, 1が裏だとすると

表が出る確率が1/2になる確率は、(1,0)(0,1)の時だけなので、1/2

4回投げる

表が出る確率が1/2になる確率は、6/16(37.5%)
6 = 4C2 = 4*3/2
16 = 2^4

Rで計算してみる

Rのセットアップ

https://cran.r-project.org/bin/macosx/ からインストール

choose(4, 2) => 6
2**4 => 16

コインの表が出る確率を実験する(R編)

8回投げる

11110000

> choose(8, 4)/2**8
[1] 0.2734375

11111000

> choose(8, 5)/2**8
[1] 0.21875

11111100

> choose(8, 6)/2**8
[1] 0.109375

11111110

> choose(8, 7)/2**n
[1] 0.03125

11111111

> choose(8, 8)/2**n
[1] 0.00390625

表が出る確率が1/2(50%)になる確率は、27.3%
表が出る確率が5/8(63.5%)になる確率は、21.9%
表が出る確率が6/8(75%)になる確率は、10.9%
表が出る確率が7/8(87.5%)になる確率は、3.1%
表が出る確率が8/8(100%)になる確率は、0.4%

表が出る確率が3/8(37.5%)になる確率は、21.9%
表が出る確率が2/8(25%)になる確率は、10.9%
表が出る確率が1/8(12.5%)になる確率は、3.1%
表が出る確率が0/8(0%)になる確率は、0%

dbinomの使い方

8枚投げて4枚表。50％の確率のもの。

choose(8, 4)/2**8
[1] 0.2734375
dbinom(4, 8, 0.5)
[1] 0.2734375
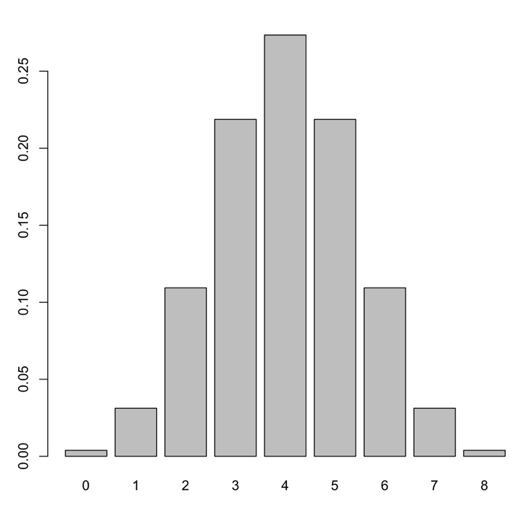
barplot(dbinom(0:8,8,0.5), names.arg=0:8)

pbinom(0:8,8,0.5)
[1] 0.00390625 0.03515625 0.14453125 0.36328125 0.63671875 0.85546875 0.96484375
[8] 0.99609375 1.00000000
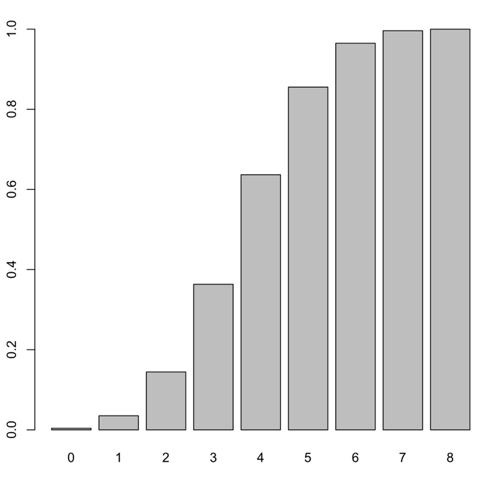
barplot(pbinom(0:8,8,0.5), names.arg=0:8)

sum(dbinom(3:5,8,0.5))
[1] 0.7109375
sum(dbinom(2:6,8,0.5))
[1] 0.9296875

・8回のコインを投げると、71%の確率で、3-5枚表になる
・8回のコインを投げると、92%の確率で、2-6枚表になる

自分でやってみよう

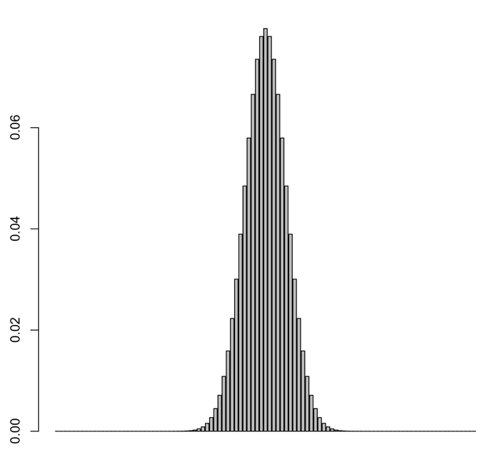
コインを100, 1000, 10000枚投げるとどうなるか試してみよう

100回投げる

> n=100;r=0.01;sum(dbinom((n/2-n*r):(n/2+n*r),n,0.5))
[1] 0.2356466
> n=100;r=0.02;sum(dbinom((n/2-n*r):(n/2+n*r),n,0.5))
[1] 0.3827006
> n=100;r=0.03;sum(dbinom((n/2-n*r):(n/2+n*r),n,0.5))
[1] 0.5158816
> n=100;r=0.04;sum(dbinom((n/2-n*r):(n/2+n*r),n,0.5))
[1] 0.6317984
> n=100;r=0.05;sum(dbinom((n/2-n*r):(n/2+n*r),n,0.5))
[1] 0.728747
> n=100;r=0.06;sum(dbinom((n/2-n*r):(n/2+n*r),n,0.5))
[1] 0.8066521
> n=100;r=0.07;sum(dbinom((n/2-n*r):(n/2+n*r),n,0.5))
[1] 0.8667894
> n=100;r=0.08;sum(dbinom((n/2-n*r):(n/2+n*r),n,0.5))
[1] 0.9113739
> n=100;r=0.09;sum(dbinom((n/2-n*r):(n/2+n*r),n,0.5))
[1] 0.9431121
> n=100;r=0.10;sum(dbinom((n/2-n*r):(n/2+n*r),n,0.5))
[1] 0.9647998

・100回のコインを投げると、52%の確率で、47-53枚になる
・100回のコインを投げると、81%の確率で、44-56枚になる
言い換えると
・100回のコインを投げると、52%の確率で、47-53枚になる
-> 48%の確率で、46枚以下54枚以上になる
-> 48%の確率で、4%以上本来の確率(50%)から値が離れる

・100回のコインを投げると、81%の確率で、44-56枚になる
-> 19%の確率で、43枚以下57枚以上になる
-> 19%の確率で、7%以上本来の確率(50%)から値が離れる

練習

1000回のコインを投げると、50%, 49-51%, 48-52%, 47-53%になる確率は？
10000回のコインを投げると、50%, 49.5-50.5%, 49-51%になる確率は？

伝えたいこと

コインを投げても、結果は1/2にならない
100回投げても、19%の確率で、本来の確率より7%以上値が離れる
偶然起きるとはなにか、どのくらいの頻度で起きるか
次は、p値とはなにか。信頼区間をどう計算するか

偶然とはなにか。コインを投げてみよう