自分の勉強のため.
中はRで書かれてるのでそれをPythonに書き換えて頑張る.
コード中のコメントアウトはR言語.
2.1 例題:種子数の統計モデリング
Rには種子数のカウントデータがあるらしい.
多分numpy,pandasを使って処理した方がいい気がするから,
numpy.arrayとpandas.Seriesそれぞれでもデータを用意.
あとグラフ用にpyplotも.
>>> data = [2, 2, 4, 6, 4, 5, 2, 3, 1, 2, 0, 4, 3, 3, 3, 3, 4, 2, 7, 2, 4, 3, 3, 3, 4, 3, 7, 5, 3, 1, 7, 6, 4, 6, 5, 2, 4, 7, 2, 2, 6, 2, 4, 5, 4, 5, 1, 3, 2, 3]
>>> import numpy
>>> import pandas
>>> matplotlib.pyplot as plt
>>> ndata = numpy.asarray(data)
>>> pdata = pandas.Series(data)
種子数は50個.
# length(data)
>>> len(data)
50
>>> len(ndata)
50
>>> len(pdata)
50
データの標本平均や最小値・最大値・四分位数などを表示するには
# summary(data)
>>> pdata.describe()
count 50.00000
mean 3.56000
std 1.72804
min 0.00000
25% 2.00000
50% 3.00000
75% 4.75000
max 7.00000
dtype: float64
度数分布を取得する
# table(data)
>>> pdata.value_counts()
3 12
2 11
4 10
5 5
7 4
6 4
1 3
0 1
dtype: int64
種子数5は5個体,種子数6は4個体であることを確認できる.
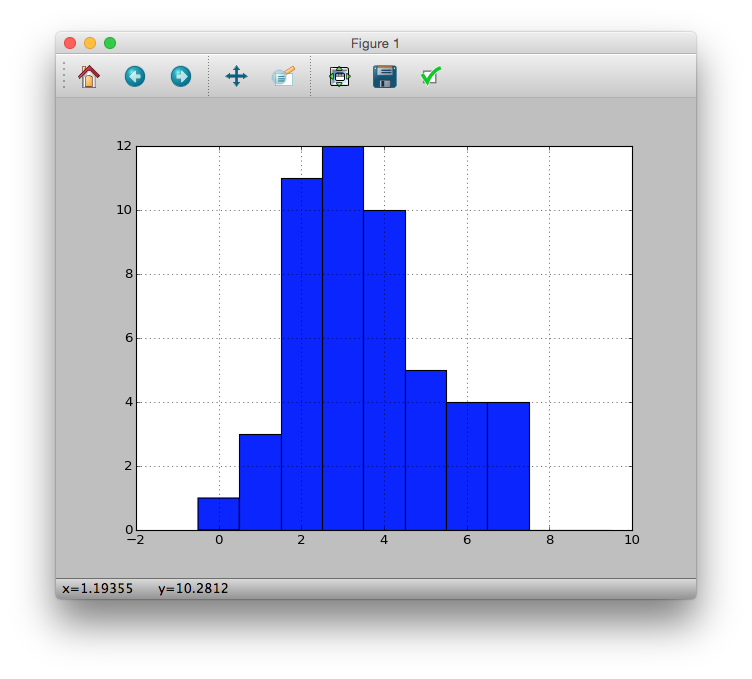
これをヒストグラムで表示する
# hist(data, breaks = seq(-0.5, 9.5, 1))
>>> pdata.hist(bins=[i - 0.5 for i in xrange(11)])
<matplotlib.axes._subplots.AxesSubplot object at 0x10f1a9a10>
>>> plt.show()
データのばらつきを表す統計量”標本分散”の算出.
numpyとpandasでデフォルトの分散の計算方法が違うらしい.(参考)
ちなみにRの場合は不偏推定量っぽい.
# var(data)
>>> numpy.var(ndata) # 標本統計量
2.9264000000000006
>>> numpy.var(ndata, ddof=True) # 不偏推定量
2.9861224489795921
>>> pdata.var() # 不偏推定量
2.986122448979593
>>> pdata.var(ddof=False) # 標本統計量
2.926400000000001
標準偏差のほうも分散と同様の挙動を示す模様.
今回はpandasの例だけ.
# sd(data)
>>> pdata.std()
1.7280400600042793
# sqrt(var(data))
2.2 データと確率分布の対応関係をながめる
種子数データには以下の特徴があることがわかる.
- 1個,2個,...と数えられるカウントデータ
- 1個体の種子数の標本平均は$3.56$
- 個体ごとの趣旨ううにはばらつきがあり,ヒストグラムを描くと一山の分布になる
ばらつきを表すため,確率分布を使う.
種子数データを統計モデルとして表現するために,
今回はポアソン分布を用いるらしい.
ある植物個体$i$の種子数$y_i$を確率変数と呼ぶ.
個体1の種子数$y_1=2$となりうる確率はどれくらいか?
を表現する確率分布は比較的簡単な数式で定義され,パラメータによってその形が決定する.
ポアソン分布の場合は,パラメータは分布の平均のみ.
今回の例題で言えば,平均$3.56$のポアソン分布となる.
分布関係はscipyがいいっぽい.
# y <- 0:9
# prob <- dpois(y, lambda = 3.56)
# plot(y, prob, type="b", lyt=2)
>>> import scipy.stats as sct
>>> y = range(10)
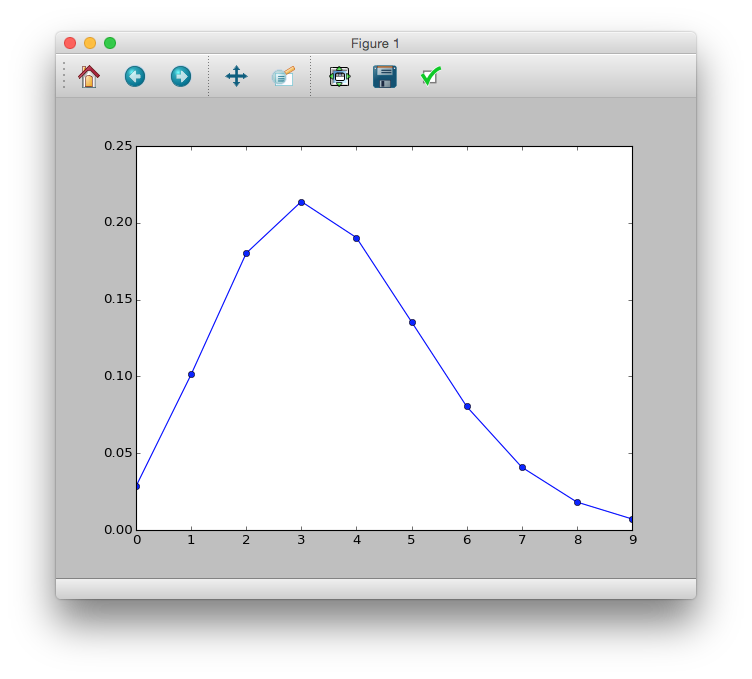
>>> prob = sct.poisson.pmf(y, mu=3.56)
>>> plt.plot(y, prob, 'bo-')
>>> plt.show()
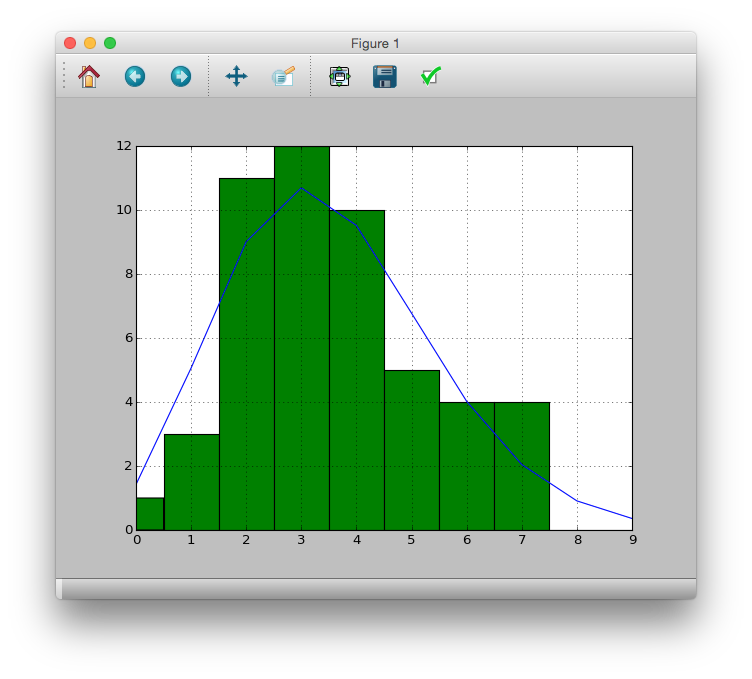
実際のデータと重ね合わせてみる
>>> pdata.hist(bins=[i - 0.5 for i in range(11)])
>>> pandas.Series(prob*50).plot()
>>> plt.plot()
この結果ならポアソン分布で観察データを表現できていると考えられる.
2.3 ポアソン分布とは何か?
ポアソン分布についてもう少し詳しく.
ポアソン分布の定義
平均が$\lambda$であるときの確率変数が$y$であるときの確率
p(y|\lambda) = \frac{\lambda ^{y}\exp(-\lambda)}{y!}
性質
- $\lambda$の値によって曲線の形が変わる
- $y \in${$0, 1, 2, \dots,\infty$}の値をとり,全ての$y$について
\sum^{\infty}_{y=0}p(y|\lambda) = 1
- 確率分布の平均は$\lambda$である($\lambda \geq 0$)
- 分散と平均は等しい
ポアソン分布を今回選んだ理由
- データに含まれている値$y_i$が非負の整数である(カウントデータである)
- $y_i$に下限(0)はあるが,上限はない
- 観測データの平均と分散がほぼ等しい
2.4 ポアソン分布のパラメータの最尤推定
最尤推定法
尤度と呼ばれるモデルの「当てはまりの良さ」を表す統計量を決める手法.
ポアソン分布の場合は$\lambda$を決める.
ある$\lambda$が決まった場合の全ての個体$i$についての確率$p(y_i|\lambda)$の積
尤度は$L(\lambda)$と表記される.
今回の場合は,
\begin{eqnarray*}
L( \lambda ) &=& (y_1が2である確率) \times (y_2が2である確率) \times \dots \times (y_50が3である確率)\\
&=& p(y_1 | \lambda) \times p(y_2 | \lambda) \times p(y_3 | \lambda) \times \dots \times p(y_50 | \lambda)\\
&=& \prod_{i}p(y_i | \lambda) = \prod_{i} \frac{\lambda^{y_i} \exp (-\lambda)}{y_i !}
\end{eqnarray*}
となる.50個の個体が観測と同じになる確率(=50個の事象が真である確率)を計算するため,積にする.
尤度関数$L(\lambda)$のままだと使いにくいため,大体は対数尤度関数(log likelihood function)を使う.
\begin{eqnarray*}
\log L(\lambda) &=& \log \left( \prod_{i} \frac{\lambda^{y_i} \exp (-\lambda)}{y_i !} \right) \\
&=& \sum_i \log \left( \frac{\lambda^{y_i} \exp (-\lambda)}{y_i !} \right) \\
&=& \sum_i \left( \log(\lambda^{y_i} \exp (-\lambda)) - \log y_i ! \right)\\
&=& \sum_i \left( y_i \log \lambda - \lambda - \sum^{y_i}_{k} \log k \right)
\end{eqnarray*}
この対数尤度$\log L(\lambda)$と$\lambda$の関係をグラフにする.
# logL <- function(m) sum(dpois(data, m, log=TRUE))
# lambda <- seq(2, 5, 0.1)
# plot(lambda, sapply(lambda, logL), type="l")
>>> logL = lambda m: sum(sct.poisson.logpmf(data, m))
>>> lmd = [i / 10. for i in range(20, 50)]
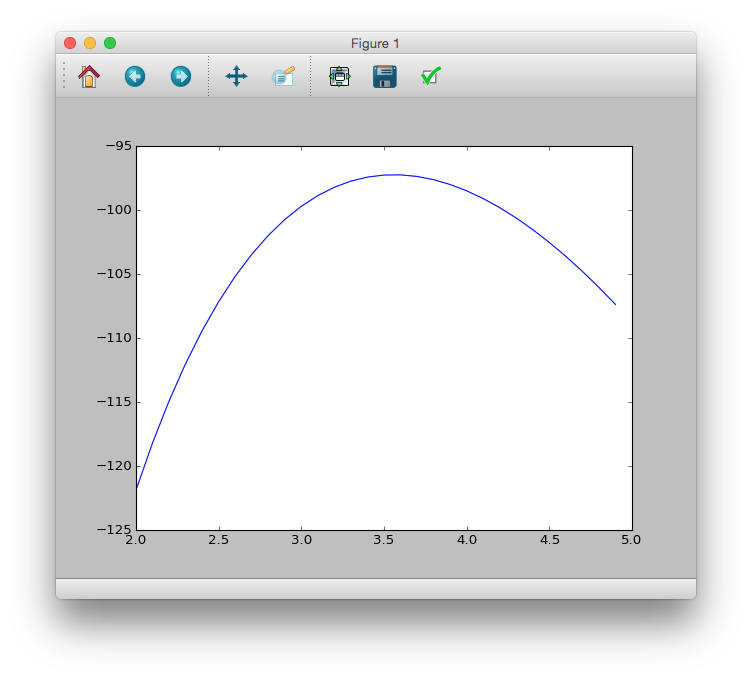
>>> plt.plot(lmd, [logL(m) for m in lmd])
>>> plt.show()
対数尤度$\log L(\lambda)$は尤度$L(\lambda)$の単調増加関数であるから,
対数尤度が最大のとき,尤度も最大となる.
グラフを見た感じ最も確率が高いのは,$\lambda = 3.5$付近ということがわかる.
具体的な最大値は対数尤度の極大値を求めれば良い(=傾きが0になるとき)
つまり,
\begin{eqnarray*}
\frac{\partial \log L(\lambda)}{\partial \lambda} = \sum_i \left\{ \frac{y_i}{\lambda} - 1 \right\} = \frac{1}{\lambda} \sum_i y_i - 50 &=& 0 \\
\lambda &=& \frac{1}{50}\sum_i y_i \\
&=& \frac{全部のy_iの和}{データ数}(=データの標本平均) \\
&=& 3.56
\end{eqnarray*}
となり,対数尤度および尤度が最大になる$lambda$を最尤推定量,具体的な$y_i$で評価された$\lambda$を最尤推定値と呼ぶ.
一般化
$\theta$をパラメータとする確率分布から観測データ$y_i$が発生した場合の確率を$p(y_i | \theta)$とすると,
尤度,対数尤度は
\begin{eqnarray*}
L(\theta | Y) &=& \prod_i p(y_i | \theta) \\
\log L(\theta | Y) &=& \sum_i \log p(y_i | \theta)
\end{eqnarray*}
となる.
確率分布の選びかた
次の点について考える.
- 説明したい量は離散か連続か?
- 説明したい量の範囲は?
- 説明したい量の標本平均と標本分散の関係は?
カウントデータの統計モデルで用いる分布の例として:
- ポアソン分布:データが離散値,ゼロ以上の範囲,上限特になし, 平均$\approx$分散
- 二項分布:データが離散値,ゼロ以上で有限の範囲${0, 1, 2, \dots, N}$,分散は平均の関数
また連続分布については
- 正規分布:データが連続値,範囲が$[-\infty, +\infty]$,分散は平均とは無関係に決まる
- ガンマ分布:データが連続値,範囲が$[0, +\infty]$,分散は平均の関数
- 一様分布:データが連続値,有界