前回(2章)に引き続いて,3章.
説明変数を組み込んだ統計モデルについての勉強.
3.1 例題:個体ごとに平均種子数が異なる場合
前回との差分として,個体の属性のひとつである体サイズ$x_i$とコントロールの有無(何もしていない:C,肥料を加える:T)を説明変数として用いる.
データの読み込み
ここの3章のところのdata3a.csvをダウンロードして使う.
今回使うデータはDataFrame型と呼ばれるやつ.
# d <- read.csv("data3a.csv")
>>> import pandas
>>> d = pandas.read_csv("data3a.csv")
>>> d
y x f
0 6 8.31 C
1 6 9.44 C
2 6 9.50 C
3 12 9.07 C
...(中略)...
98 7 10.86 T
99 9 9.97 T
[100 rows x 3 columns]
# d$x
>>> d.x
0 8.31
1 9.44
2 9.50
...(中略)...
98 10.86
99 9.97
Name: x, Length: 100, dtype: float64
# d$y
>>> d.y
0 6
1 6
2 6
...(中略)...
98 7
99 9
Name: y, Length: 100, dtype: int64
# d$f
>>> d.f = d.f.astype('category')
>>> d.f
0 C
1 C
2 C
3 C
...(中略)...
98 T
99 T
Name: f, Length: 100, dtype: category
Categories (2, object): [C < T]
Rではf列のことを因子(factor)と呼ぶらしいけど,
python(pandas)ではcategoryになってる.
データの型を確認するには
# class(d)はちょっと確認できず.
# class(d$y)やらclass(d$x)やらclass(d$f)
>>> d.y.dtype
dtype('int64')
>>> d.x.dtype
dtype('float64')
>>> d.f.dtype
dtype('O')
データフレームの概要は,Series(前回のと一緒)
# summary(d)
>>> d.describe()
y x
count 100.000000 100.000000
mean 7.830000 10.089100
std 2.624881 1.008049
min 2.000000 7.190000
25% 6.000000 9.427500
50% 8.000000 10.155000
75% 10.000000 10.685000
max 15.000000 12.400000
>>> d.f.describe()
count 100
unique 2
top T
freq 50
Name: f, dtype: object
可視化
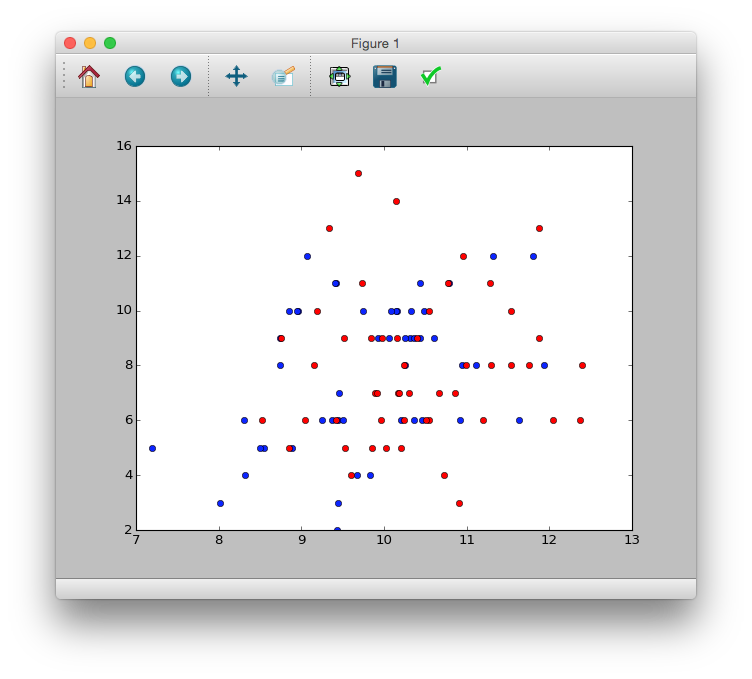
Rみたいに一行で散布図を色分ける方法が見つからず...
# plot(d$x, d$y, pch=c(21, 19)[d$f])
>>> plt.plot(d.x[d.f == 'C'], d.y[d.f == 'C'], 'bo')
[<matplotlib.lines.Line2D at 0x1184d0490>]
>>> plt.plot(d.x[d.f == 'T'], d.y[d.f == 'T'], 'ro')
[<matplotlib.lines.Line2D at 0x111b58dd0>]
>>> plt.show()
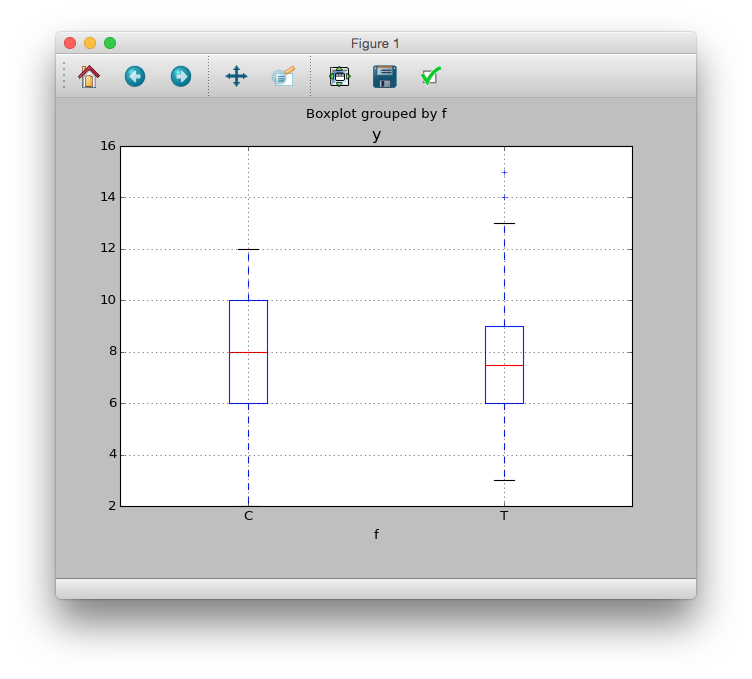
>>> d.boxplot(column='y', by='f')
<matplotlib.axes._subplots.AxesSubplot at 0x11891a9d0>
これらの図からわかることは
- 体サイズ$x_i$が増加するにつれ,種子数$y$が増加しているように見える
- 肥料の効果$f$はないように思われる
ポアソン回帰の統計モデル
カウントデータである種子数データをうまく表現できそうな統計モデルをつくる.
個体$i$の体サイズ$x_i$に依存する統計モデル
説明変数:$x_i$
応対変数:$y_i$
ある個体$i$において種子数が$y_i$である確率$p(y_i|\lambda_i)$はポアソン分布にしたがっていて,
p(y_i|\lambda_i) = \frac{\lambda _i ^{y_i} \exp (-\lambda_i)}{y_i !}
と仮定する.
ここで,ある個体$i$の平均種子数$\lambda_i$が
\begin{eqnarray}
\lambda_i &=& \exp(\beta_1 + \beta_2 x_i )
\log \lambda_i &=& \beta_1 + \beta_2 x_i
\end{eqnarray}
であるとする.
$\beta_1$を切片,$\beta_2$は傾きとよび,
右辺$\beta_1 + \beta_2 x_i$を線形予測子とよぶ.
また($\lambda_i$の関数)=(線形予測子)となっている場合,
左辺の関数はリンク関数と呼ばれる.
ポアソン回帰
ポアソン回帰は以下の式が最大となる$\beta_1, \beta_2$を見つけること.
\log L(\beta_1, \beta_2) = \sum_i \log \frac{\lambda_i^{y_i}\exp(-\lambda_i)}{y_i !}
Rだとglmとかいうのを使えば一発らしい.
pythonだとstatsmodelsライブラリを使って延々と頑張らないといけないとか,,,(参考)
# fit <- glm(y ~ x, data=d, familiy=poisson)
>>> import statsmodels.api as sm
>>> import statsmodel.formula.api as smf
>>> model = smf.glm('y ~ x', data=d family=sm.families.Poisson())
>>> results = model.fit()
>>> print(results.summary())
Generalized Linear Model Regression Results
==============================================================================
Dep. Variable: y No. Observations: 100
Model: GLM Df Residuals: 98
Model Family: Poisson Df Model: 1
Link Function: log Scale: 1.0
Method: IRLS Log-Likelihood: -235.39
Date: 月, 01 6 2015 Deviance: 84.993
Time: 23:06:45 Pearson chi2: 83.8
No. Iterations: 7
==============================================================================
coef std err z P>|z| [95.0% Conf. Int.]
------------------------------------------------------------------------------
const 1.2917 0.364 3.552 0.000 0.579 2.005
x 0.0757 0.036 2.125 0.034 0.006 0.145
==============================================================================
>>> results.llf
-235.38625076986077
RではInterceptってなってるらしいけど,
Pythonでは一番下のconstが$\beta_1$(切片),xが$\beta_2$(傾き)を表しているらしい.
つまり,最尤推定量は$\beta_1=1.2917$と$\beta_2=0.0757$ということ.
std errは標準誤差を示していて,$\beta_1, \beta_2$のばらつきを示している.
同じ調査方法で同数の別データをサンプリングしなおすと,最尤推定量も変わり,そのばらつき具合
zはz値という統計量で,最尤推定量を標準誤差で割ったもの.
このzによってWald信頼区間というものが推定できるらしい
この信頼区間はどうやら,最尤推定量が取りうる値に0が入らないということっぽい参照
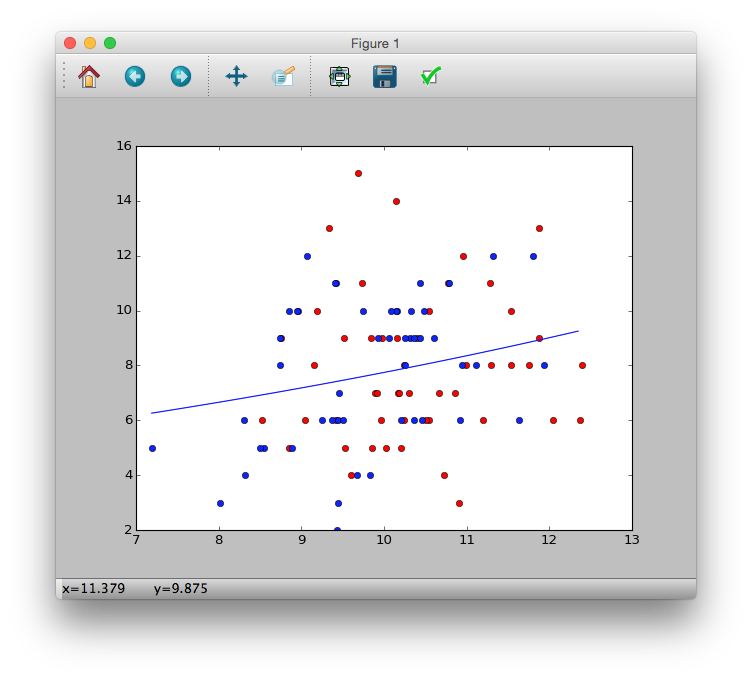
ポアソン回帰モデルによる予測
ポアソン回帰の推定結果を使って,体サイズ$x$における平均種子数$\lambda$を予測する.
\lambda = \exp(1.29 + 0.0757x)
を用いて図示する.
# plot(d$x, d$y, pch=c(21, 19)[d$f])
# xx <- seq(min(d$x), max(d$x), length=100)
# lines(xx, exp(1.29 + 0.0757 * xx), lwd = 2)
>>> plt.plot(d.x[d.f == 'C'], d.y[d.f == 'C'], 'bo')
>>> plt.plot(d.x[d.f == 'T'], d.y[d.f == 'T'], 'ro')
>>> xx = [d.x.min() + i * ((d.x.max() - d.x.min()) / 100.) for i in range(100)]
>>> yy = [numpy.exp(1.29 + 0.0757 * i )for i in xx]
>>> plt.plot(xx, yy)
>>> plt.show()
3.5 説明変数が因子型の統計モデル
施肥処理$f_i$を説明変数として組み込んだ統計モデルを考える.
因子型の説明変数はGLMの中では,ダミー変数を用いる.
つまり,モデルの平均値を,
\begin{eqnarray}
\lambda_i &=& \exp (\beta_1 + \beta_3 d_i) \\
\therefore d_i &=& \left\{ \begin{array}{ll}
0 & (f_i = Cの場合) \\
1 & (f_i = Tの場合)
\end{array} \right.
\end{eqnarray}
と書くことになる.
# fit.f <- glm(y ~ f, data=d, family=poisson)
>>> model = smf.glm('y ~ f', data=d, familiy=sm.families.Poisson())
>>> model.fit().summary()
Generalized Linear Model Regression Results
==============================================================================
Dep. Variable: y No. Observations: 100
Model: GLM Df Residuals: 98
Model Family: Poisson Df Model: 1
Link Function: log Scale: 1.0
Method: IRLS Log-Likelihood: -237.63
Date: 木, 04 6 2015 Deviance: 89.475
Time: 17:20:11 Pearson chi2: 87.1
No. Iterations: 7
==============================================================================
coef std err z P>|z| [95.0% Conf. Int.]
------------------------------------------------------------------------------
Intercept 2.0516 0.051 40.463 0.000 1.952 2.151
f[T.T] 0.0128 0.071 0.179 0.858 -0.127 0.153
==============================================================================
>>> model.llf
-237.62725696068682
この結果から,もし個体$i$の$f_i$がCならば,
\lambda_i = \exp(2.05 + 0.0128 * 0) = \exp(2.05) = 7.77
もしTならば,
\lambda_i = \exp(2.05 + 0.0128 * 1) = \exp(2.0628) = 7.87
となり,肥料を与えると平均種子数がほんの少しだけ増加すると予測している.
対数尤度(llf)については,小さくなってしまっているため,あてはまりが悪いといえる.
3.6 説明変数が数量型 + 因子型の統計モデル
個体の体サイズ$x_i$と施肥処理$f_i$の両方を組み込んだ統計モデルを考える.
\log \lambda_i = \beta_1 + \beta_2 x_i + \beta_3 d_i
>>> model = smf.glm('y ~ x + f', data=d, family=sm.families.Poisson())
>>> result = model.fit()
>>> result.summary()
Generalized Linear Model Regression Results
==============================================================================
Dep. Variable: y No. Observations: 100
Model: GLM Df Residuals: 97
Model Family: Poisson Df Model: 2
Link Function: log Scale: 1.0
Method: IRLS Log-Likelihood: -235.29
Date: 木, 04 6 2015 Deviance: 84.808
Time: 17:31:34 Pearson chi2: 83.8
No. Iterations: 7
==============================================================================
coef std err z P>|z| [95.0% Conf. Int.]
------------------------------------------------------------------------------
Intercept 1.2631 0.370 3.417 0.001 0.539 1.988
f[T.T] -0.0320 0.074 -0.430 0.667 -0.178 0.114
x 0.0801 0.037 2.162 0.031 0.007 0.153
==============================================================================
>>> result.llf
-235.29371924249369
最大対数尤度は最も大きいことから,上記2つの統計モデルよりあてはまりが良いといえる.
対数リンク関数のわかりやすさ:掛け算される効果
上記の数量型 + 因子型の統計モデルの数式を変形すると,
\begin{eqnarray}
\log \lambda_i &=& \beta_1 + \beta_2 x_i + \beta_3 d_i \\
\lambda_i &=& \exp(\beta_1 + \beta_2 x_i + \beta_3 d_i) \\
\lambda_i &=& \exp(\beta_1) * \exp(\beta_2 x_i) * \exp(\beta_3 d_i) \\
\lambda_i &=& \exp(定数) * \exp(体サイズの効果) * \exp(施肥処理の効果)
\end{eqnarray}
と表せ,効果が掛け合わされているのがわかる.
リンク関数がなにもない場合,恒等リンク関数と呼ぶ.
GLMにおいて
正規分布かつ,口頭リンク関数の場合を 線形モデル(linear model, LM)もしくは一般線形モデル(general linear model)と呼ぶ.