「数学なんて将来何の役に立つの？」という疑問に対するウェブデザイナーの回答一覧 #プログラミング

反抗期のお子さまをお持ちのみなさまはさぞ教育に苦労されていることでしょう。この記事が（実際半分以上がネタ項目ですが）少しでもお役に立てれば幸いです。¹

小学校「算数科」

四則演算・九九・分数・小数

これはフロントエンドに限らずすべてのプログラミング言語の基礎になるから、わかるようになってよかったね。（それ以前に普通に日常生活で使うけど。）

日付・時間（時刻）

new Date() した結果を24時間表記にしたり、「月日」など漢字単位区分を含んだString型に変換したりするための基礎になるから大事だね。あと、電車が来る時間がわかって会社に遅れずに済んだり（そもそも「遅れる」という概念を理解したり）、アジャイル開発における工数管理の指標定義ができるようになるね。

平面図形

一辺の長さが 0 の場合は二次元にならないということから、CSSで図形を書かなければいけないことがあったら、width と height に 0より大きい正の数を指定すればいいということがわかったね。

立体図形

立体図形の概念を学んだということは、ブラウザ上での3Dレンダリングが必要になっても大丈夫だね。 transform: translate3d() / translateZ() や transform: rotate3d() / rotateZ() が使えると楽しくなるね。

X軸、Y軸、Z軸、X+Y軸、X+Y+Z軸での回転例
https://codepen.io/kyoyababa/pen/KmLNPP

概数・四捨五入

Math.floor() と Math.round() と Math.ceil() の違いがわかったね。ファイルサイズや現在時刻を丸めていい感じに表示したらユーザーも喜ぶよね。

JavaScript

Math.floor(3.33); // => 3
Math.floor(6.66); // => 6

Math.round(3.33); // => 3
Math.round(6.66); // => 7

Math.ceil(3.33);  // => 4
Math.ceil(6.66);  // => 7

角度

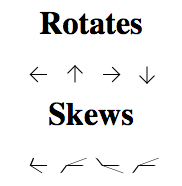
transform: rotate() や transform: skew() で指定する値の意味がわかったね。
あと、例えば矢印の画像を 90deg ごとに回転させて、ひとつの画像で四方向ぶんのレンダリングができたりするから便利だね。

Rotationについては, 左から, rotate(0deg) / rotate(90deg) / rotate(180deg) / rotate(270deg) のtransform例. Skewは観測者の目線の移動を角度で示したもの. 左から, skew(30deg) / skew(120deg) / skew(210deg) / skew(300deg)
https://codepen.io/kyoyababa/pen/wdbJGy

奇数と偶数・約数と倍数

列ごと・行ごとにスタイルを変えたいことって静的・動的いずれの開発でもけっこうあることなんだよね。
tr:nth-child(even) や tr:nth-child(odd) 、 tr:nth-child(3n) みたいなスタイル反映はすでに標準的だから覚えておいて損はないよね。

円周率

Math.pi() で出てくる謎の小数の意味がわかったということだね。
授業では円周の長さと面積を求めるくらいしか習わなかったと思うけど、大きくなったら習う「平方根」や「三角関数」と組み合わせたら、いろいろなDOM操作ができるようになるよ。（三角関数の項で後述）

縮図や拡大図

transform: scale() での図形の拡大・縮小の割合を計算できるようになったね。

比例・反比例

画像や動画のアスペクト比をもとに表示サイズを最適化したい、なんてことよくあるよね。
たとえば、16:9 の画像を横幅 200pxで表示したいとき、高さは calc(200px * 9 / 16) として求められるということがわかったから、応用することで「他の人が意味がわからない数値をハードコーディングしない」つまり、ほかの開発者が見たときに意味がわかるから助かるね。

場合分け

ユーザーやステータスなどの操作や状態によって処理内容を分岐するのはプログラミングの基本だよね。
与えられた条件によって処理を分岐したいなら switch() 文が使えるし、単一条件処理や条件がより複雑な場合は if() 文で場合分けができるようになったね。
「どんな場合が存在し、どの場合の割合が高いのか」を感覚的につかめると、きれいなコードが書けるひとつのきっかけになるよね。

中学校「数学科」

負の数の四則演算

position: absolute / fixed で配置した要素を領域の外側にはみ出させたいときなんかは top: -50px; left: -50px; なんてことができるけど、これは負の値を現在値 0 に足しているっていうことだ、と理解できたね。
その処理を２回繰り返したら、それぞれ -50px * 2 => -100px という結果になることがわかったね。実際、負の数の加減乗除はよく使うから大事だね。

文字式

たとえばサイドバーを画面に固定して、ヘッダーとフッターに重ならないように配置したいことなんてよくあるけど、このとき「ヘッダーとフッターの高さ」を文字（変数）として格納しておくと、ほかの開発者が見たときに意味がわかるから助かるね。²

CSS

:root {
  --header-height: 50px;
  --footer-height: 75px;
  --sidebar-width: 250px;
  --sidebar-padding: 20px;
}

.sidebar {
  position: fixed;
  top: var(--header-height);
  left: 0;
  bottom: var(--footer-height);
  width: calc(var(--sidebar-width) - var(--sidebar-padding));
}

SCSS

$header-height: 50px;
$footer-height: 75px;
$sidebar-width: 250px;
$sidebar-padding: 20px;

.sidebar {
  position: fixed;
  top: $header-height;
  left: 0;
  bottom: $footer-height;
  width: calc(#{$sidebar-width - $sidebar-padding});
}

等式・不等式

if() 文や三項演算子など、等式・不等式の評価式での比較はこれもプログラミング言語の基本中の基本だね。

作図・合同

ペンと定規での作図は普通にワイヤーフレームを描くセンスとか、イラストレータでの図形描画の感覚が身につく気がするから、意外と意味がありそう。
また、合同の意味を理解しておくと、「シャローコピーとディープコピー」「代入した変数や操作後のDOMの等価性」などの概念の感覚をつかむきっかけになりそうだね。

平面図形の移動

要素を transform: translate() で移動したり、 transform: rotate() で回転させることができるようになったね。

立体図形とその移動

立体図形がアニメーションできるようになると、仕事で役に立つことがある（はず）だよ。

translate() で描画した立体図形を rotate() で回転させるアニメーションの実装例.
https://codepen.io/kyoyababa/pen/mmQOZp

投影図

投影図の概念は、上記の「立体図形とその移動」などを論理的に理解するための手助けになるね。
ユーザの目線（モニターの表面をZ軸の最大値とした場合）とオブジェクトの角度・距離を理解すると、より transform プロパティについて理解が深まるね。³
あとは、プレゼンするときにプロジェクタをどの位置に置いたら最適な表示になるとかレイアウトしてあげたら、おじさんから感謝されたりするよ。

座標

座標の概念と計算ができるということは、クリックイベントでマウスカーソルの位置やユーザがタップした位置を取得できるようになったということだね。
X座標とY座標を document.elementFromPoint(x, y); で取得して、以下のように現在のカーソル位置を取得すると、DOM操作の幅が拡がること請け合いだね。

JavaScript(ES2015)

document.body.addEventListener('click', (e) => {
    const mouseX = e.pageX;
    const mouseY = e.pageY;
});

誤差、近似

グーグルの もしかして サジェストなんかは（機械学習とその）近似値の応用例だけど、たとえば与えられた数値から、配列に含まれる近似値を返すなんて処理が思いついたら、ウェブアプリケーションのユーザビリティ向上のアイデアになるかもしれないね。

TypeScript

/**
 * 与えられた任意の数 n の、任意の配列 arr に含まれる近似値を返す。エラーハンドリングや型判定は割愛
**/
public getApproximation(n: number, arr: Array<number>): number {
  let approximation: number = arr[0];

  for (let i: number = 1; i < arr.length; i++) {
    const diffByOldApproximation: number = Math.abs(n - approximation);
    const diffByNewApproximation: number = Math.abs(n - arr[i]);

    if (diffByNewApproximation < diffByOldApproximation) approximation = arr[i];
  }

  return approximation;
}

式変形

式変形ができるようになったということは、クソコードに出会ったときに最適化できる能力が身についたということだね。
さらに、 a > b なのか b < a なのか（意味は一緒だが、ビジネスロジックとしてどちらが最適か）を考えられるようになるためには、式変形ができるようになっていないといけないよね。

百分率・確率・樹形図

百分率がわかると、CSSの opacity や filter プロパティの小数値指定の意味がわかるようになるね。
また、確率の概念を理解していれば Math.random() と任意の係数を組み合わせて、いわゆる「ガチャ」の実装もできるね。
そして、樹形図を書くのに慣れたらサイトマップやドメイン概念図を書くのに役立つね。

平方根

平方根の概念がわかれば、斜めに横切る要素の長さを指定できるようになるよ。
たとえば、親要素に対して、5の平方根での割合を縦横サイズとした子要素を作る場合、以下のように記述すれば五角形の一辺の長さとしてレンダリングできる。

SCSS

.pentagon__side {
  // √(5 - 2√5) * 100%
  width: sqrt(5 - 2 * sqrt(5)) * 100%;
}

さらにそれを５つの子要素として展開すれば、五角形を描画できるね。

SCSS

@for $i from 0 through 5 - 1 {
  .pentagon__side:nth-of-type(#{$i + 1}) {
    transform: rotate(360deg / 5 * $i); // => 72deg * $i
  }
}

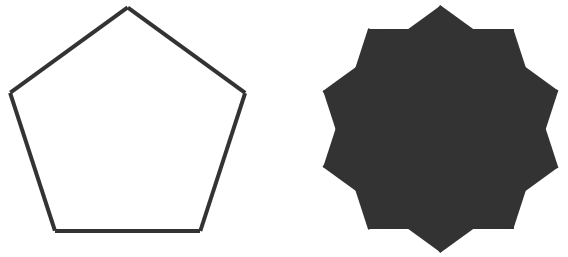
このままだと何も表示されないから、（いい感じに位置を調整してから） border-top / border-bottom を指定すれば、SVGに頼らずとも⁴五角形が描けるということだね。ちなみに、この状態で border ではなく background-color を指定すると10角形になる。

親要素に対して5の平方根での割合を縦横サイズに指定した五角形と10角形のレンダリング. 10角形を塗りつぶしではなく境界線のみで描画したい場合は、子要素のサイズを10の平方根で指定する必要がある.
https://codepen.io/kyoyababa/pen/dWQvPg

因数分解

因数分解とはすなわち「和と差の積に展開」することだから、与えられた値をもとに変数を推測できるようになったね。
たとえば「年収を月収に変換する」とき、ボーナスが年２回×１ヶ月ぶんずつ支給される前提だと、以下のようになるということがわかるね。

TypeScript

public convertYearSalaryToMonthSalary(yearSalary: number, bonusLength?: number): number {
  if (typeof bonusLength === 'undefined' || bonusLength < 0) bonusLength = 2;

  // 因数分解すると monthSalary * 12 + monthSalary * 2 = yearSalary; なので
  return yearSalary / (12 + bonusLength);
}

高等学校「数学科」IA, IIB

循環小数

循環小数の概念を学んだということは、 width: 33.33% と書くのは厳密ではない、ということがわかったね。この場合、 width: calc(100% / 3) と書けばブラウザがよしなに表示してくれるから助かるね。

絶対値

Math.abs() で絶対値を求められると知っておけば * -1 するよりなんとなくかっこいい感じがするし、そもそも変数が正になるか負になるかわからない場合に必要だね。要素が中央値からどのくらい移動しているかといったように、上述の 誤差、近似 の項でも触れたように「相対的な数値」を測る場合に必要になるね。

冪乗

冪乗 Math.pow() は意外とよく使うんだよ。 1000000 は Math.pow(10, 6) と表すので、キロ / メガ / ギガバイトのようなファイルサイズの計算のときに便利だね。
あとこれも意外と知られていないけど、ES2015から 10 ** 6 とも書けるようになったし、 += みたいなノリで **= も使えるようになったらしいよ。

階乗

階乗はメソッドが用意されていないから（Pythonとかでは用意されてるらしいけど...）自分で作らなければいけない。意外と（プログラマの能力を図る系の）テストに出たりするから、覚えておいて損はないよ。「並べ替え・順列のパターン出し」や、「パスワードの安全性検証（文字列の組み合わせ）」のようなときに使えるね。

JavaScript(ES2015)

// 再帰構文（関数のなかでその関数を呼び出す）のため、テストに出やすい。
function factorialize(n) {
  let returnValue = 1;

  if (n > 1) returnValue = n * factorialize(n - 1);

  return returnValue;
}

f(x)関数

f(x) を覚えたということは、JavaScriptにおける function foo(bar) {} の関数が使えるようになったということも同然だね。
ただし、数学とは違って function (bar) = ... と書いたら Unexpected Token ( と怒られるから気をつけてね。ES2015だと function bar = () => {} 型になるよ。

集合

集合の概念を知っておけば、アジャイル開発における各チケットのストーリーごとの分類や横軸での関係性が視覚的に落とし込めるし、ソースコード上でも関数をグローバルに定義したときにどう呼び出すかをイメージできるような気がするね。

真偽判定、逆・裏・対偶の論証、空事象・余事象・全事象

真偽判定ができるようになったということは、以下のscriptは同義だということがわかったね。

JavaScript

if (foo) { return true; } else { return false; }

JavaScript

return !!foo;

逆・裏・対偶の関係性がわかっていれば、 !true === false という三項演算子での重要なポイントを理解したということだね。

さらに、ド・モルガンの法則によって !(p && q) と !p || !q 、 !(p || q) と !p && !q はそれぞれ同じだということがわかったから、コードレビューでいちいち評価式の書き方が微妙だと言われなくて済むようになったね。

帰納法・背理法

テストコードを書くということは、まさにこれのことだね。あと、ナンクロがうまくなるね。

三角関数

三角関数が使えるようになったら、斜めにアニメーションする要素の移動距離を、一方の座標から一方の座標を求めることが可能になったね。
あとは、たとえば「ポンデリングみたいなやつをレンダリングしなければいけない」なんてこと、よくあるよね（無い）。そんなとき、円周率と三角関数を併用すれば、円周上に任意の個数の要素を等間隔で配置できるね。

HTML&CSS

<div id="jsi-element__wrapper" class="g-element__wrapper">
  <!-- 円周上に配置したい６つの子要素 -->
  <div></div><div></div><div></div><div></div><div></div><div></div>
</div>

<style>
  .g-element__wrapper { position: relative; }
  .g-element__wrapper > div { position: absolute; width: 100px; height: 100px; border-radius: 100%; background-color: yellow; }
</style>

JavaScript(ES2015)

/**
 * 任意の要素の子要素を円周上に配置する
**/
function positionElementChildren() {
  const $wrapper = document.getElementById('jsi-element__wrapper');
  // 円の中心から各要素までの距離
  const radius = 100;

  for (let i = 0; i < $wrapper.children.length; i++){
    // 要素と要素が配置される角度の割合を求める
    const degree = 360 / $wrapper.children.length * i;
    // 上記の割合をラジアンに変換
    const radian = degree * Math.PI / 180;
    // 三角関数（正弦・余弦）を求め、X座標とY座標を決定
    const xPosition = radius * Math.cos(radian);
    const yPosition = radius * Math.sin(radian);

    $wrapper.children[i].style.transform = `translate(${xPosition}px, ${yPosition}px)`;
  }
}

上記のコードによりレンダリングした要素.
https://codepen.io/kyoyababa/pen/VbOWGY

等差数列・等比数列・階差数列

連続正解すると得点が倍増するクイズゲームを考えてみよう。初回の得点を 1点 だとした場合のクイズを n回 連続正解したときの合計得点を数列で表すと、以下のようになるね。

\sum_{k=1}^{n} 1 * 2^{k-1} = 1 + (1 * 2) + (1 * 2 * 2) + (1 * 2 * 2 * 2) + \cdots + (1 * 2^{n-1}) = 2^n-1

これにより、JavaScriptでは function (n) { return Math.pow(2, n) - 1; } すればよいということがわかるね。⁵

高等学校「数学科」IIIC

放物線・楕円・双曲線、軌跡と領域

イージング処理に用いるベジェ曲線 cubic-bezier() の関数は、広義の放物線だね。 http://cubic-bezier.com のように視覚的・感覚的に確認できるGUIが提供されているけど、 (0, 0) (1, 1) と、その間にある２種類の任意の座標をつなぐ線分が、それぞれ曲線を微分した線分になるように設計しているということがわかると、数値の理解が早まりそうだね。
また、HTML5のCanvasアニメーションでは、ある関数の「軌跡をなぞる」作業が求められることがよくあるね。よくみかける ctx.stroke(); / document.getElementById('jsi-canvas').getContext('2d').stroke() は、あらかじめその前に指定した ctx.moveTo() / ctx.lineTo() の軌跡をレンダリングしている、ということへの理解につながるね。

媒介変数、サイクロイド・アステロイド・インボリュートなどの曲線

サーバサイドエンジニアがよくつぶやいている implicit == 陰 、 explicit == 陽 の関係性がわかったね。
CSSアニメーションやイージングで用いるベジェ曲線は、媒介変数を使った関数で描かれていて、これについては以下の記事がわかりやすい。

ベジェ曲線の簡単なちょっと難しい話

それに、これらの媒介変数を用いた曲線の有名な種類を覚えておくと、デザインのクリエイティブセンスもよくなりそうなので、知っておくといいね。

媒介変数表示された有名な曲線７つ

合成関数・逆関数

f(x), g(x) の合成関数は f(g(x)) となり、 y=f(x) のときの f(x) に対する逆関数は x=g(y) となるわけだから、この変換の仕組みを知っておくと、前者は「冗長な関数群の統一（リファクタリング）」であるとか、後者は「関数やメソッドの出力結果から引数を逆算する（テスト、エラーハンドリング）」に有効な気がするね。⁶

思いつかなかったもの

微積分まわり、指数・対数・自然関数・ネーピア数、漸化式、虚数・複素数・偏角、極座標・極方程式、極限といったあたりは、さすがに有効な事例が思い浮かばなかった（すごく高度なCanvasアニメーションとかならあるのかもしれないが... Math.log() とか Math.LN2 とかをBtoBのフロント領域で使うことはあるのだろうか？）。

この辺については機械学習・深層学習に造詣のあるエンジニアがすでにPythonやJavaでの実装例や具体的な計算プロセスを複数記事にされているので参考にされたい。

タイトルに関する補足; 「数学」としているが、便宜上、小学校学習指導要領の算数・中学校学習指導要領の数学・高等学校学習指導要領の数学IA,IIB,IIICを対象とする; 「ウェブデザイナー」と明示しているのは（私が文系出身であるため）この記事ではUIデザインからフロントエンド領域までに限定するためで、線形代数や微積分を得意とする機械学習エンジニアの領域には言及しない。 ↩
余談だが、CSSのグローバル変数はブラウザ側で上書き可能で、これがSassとの決定的な違いである（Sassの変数はコンパイルされてしまうたブラウザ側では変数それ自体は上書きできない）。また、 calc() 関数内ではコンパイル時の実行とブラウザ側での実行を明示的に区別する必要があるため、特別な理由がなければ原則 #{} でStringとして出力するルールを推奨したい。 ↩
CSS transform値の設定とレンダリングに関する論理的な説明は、W3Cの公式ページを参照 ↩
最初からSVGでレンダリングしたほうが効率がいいのでは、という点については言及を控える。 ↩
とはいえ実際のプロダクトレベルであればサーバサイドから受け取る形になるだろうから、フロントでこんな実装をすることは無いだろうが。 ↩
実際にそういうアプローチでフロントエンドの保守運用をしている実例や論文を知っている方がいたらご教示願います。 ↩