この記事は#ベジェ曲線AC2015 ベジェ曲線 Advent Calendar 2015 - Adventarの13日目の記事です。
はじめに
カレンダー参加者を見る限り、イラストレーターやデザイナーの方が多いように見受けられましたが、
敢えて小難しい記事を、しかしなるべくそのような方々にも理解してもらえるように書こうと思いました。
私butchi_yは数学好きなエンジニアです。
自分自身、高校生時代だったか大学入りたての頃だったか、初めてベジェ曲線を知った時は「なんか複雑な数式…」と敬遠したりしましたが、蓋を開けてみればそんなに難しい話ではありませんでした。
ベジェ曲線の定義
Wikipediaにはこう書いてあります。
制御点を $B_0, B_1, \dots , B_{N-1}$とすると、ベジェ曲線は
$P(t) = \sum_{i=0}^{N-1} B_i J_{(N-1)i}(t)$
と表現される。ここで、 $J_{n i} t$ はバーンスタイン基底関数のブレンディング関数である。
$J_{ni}(t) = {n \choose i} t^i (1-t)^{n-i}$
$t$ が $0$ から $1$ まで変化する時、$B_0$ と $B_{N-1}$ を両端とするベジェ曲線が得られる。一般には両端以外の制御点は通らない。ベジェ曲面においては各制御点のX座標とY座標の値が一定となり、Z座標の値で制御点を扱う。
何言っているかさっぱりです。(ちゃんと読んでくれたけど理解できなかった方、無駄な時間を使わせてしまってごめんなさい。)
なんでこんな難しい説明になっているかというと、一般のN次ベジェ曲線について一般化させようとしたからなんですね。
$N=3$のときに、ちゃんと2項係数を展開させて、ベクトル表記ではなく$x$と$y$のそれぞれで表記すればこうです。
$ x(t) = t^3 x_4 + 3t^2 (1-t) x_3 + 3t(1-t)^2 x_2 + (1-t)^3 x_1 $
$ y(t) = t^3 y_4 + 3t^2 (1-t) y_3 + 3t(1-t)^2 y_2 + (1-t)^3 y_1 $
そう、3次ベジェ曲線は$t$を媒介変数とした3次多項式にすぎません。
参考: 3次ベジェ曲線の数式
CSSのcubic-bezierの場合
CSSにはcubic-bezierというイージング関数があります。
ベジェ曲線はイラストを描く以外に、アニメーション制御にも使われているのです。
以下はcubic-bezier.comというサイトでベジェ曲線を編集している画像です。

CSSにおいては、
cubic-bezier(x2, y2, x3, y3)
という指定になるので、最初から決まっている
$(x_1, y_1) = (0, 0), (x_4, y_4) = (1, 1)$
を先ほどの式に適用して、
$ x(t) = t^3 + 3t^2 (1-t) x_3 + 3t(1-t)^2 x_2 $
$ y(t) = t^3 + 3t^2 (1-t) y_3 + 3t(1-t)^2 y_2 $
と、さらに項が減ったすっきりした式になります。
それでも難しいと思ったら
具体的なベジェ曲線を与えてみましょう。
$(x_1, y_1) = (0, 0)$
$(x_2, y_2) = (0, 1)$
$(x_3, y_3) = (1, 0)$
$(x_2, y_2) = (1, 1)$
という制御点の場合、式はこうなります。
$ x(t) = t^3+3 (1-t) t^2 $
$ y(t) = t^3+3 (1-t)^2 t $
展開したらこうです。
$ x(t) = -2t^3 + 3t^2 $
$ y(t) = 4t^3 - 6t^2 + 3t $
これなら自力でもグラフを描けそうじゃないですか?
実際描いてみたらこうなります。
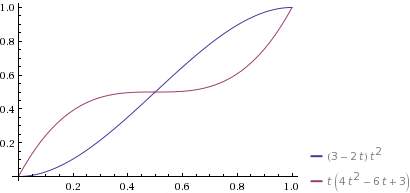
plot -2t^3 + 3t^2, 4t^3 - 6t^2 + 3t, t = 0 to 1 - Wolfram|Alpha
(↑$x, y$それぞれのグラフ)
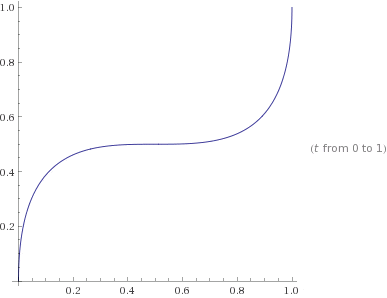
parametric plot -2t^3 + 3t^2, 4t^3 - 6t^2 + 3t, t = 0 to 1 - Wolfram|Alpha
(↑出来上がるベジェ曲線)
ちなみにこれを陽関数($y = f(x)$の形)にできないかというのが今回ベジェ曲線を考えるにあたって最初に悩んでいたことなのですが、それもある程度できなくない、という結果が出たので、いずれその話もするかもしれません。
でも、基本的には同じ$x$軸上の直線を何度も横切るタイプの曲線とかもベジェ曲線に含まれます。
さっきの例はたまたま陽関数で表せるタイプでしたが、陽関数で表すとかなり複雑な式になります。
すべてのベジェ曲線を$y = f(x)$で表すのが難しいから、基本的には媒介変数を使うというのもベジェ曲線理解のヒントになるかと思います。
終わりに
このカレンダーの参加者はベジェ愛がある人が推奨されているっぽいですが、
僕は一時期アンチベジェ曲線だったことがあり、代替となる表現方法を模索したりもしました。
でもアフィン不変性とか考えるとやっぱり好きなのかもしれません。