概要
Microsoftが作ったSAT SolverのZ3を用いて,基本的な論理素子を再現するニューラルネットワークの構築を行う.
それに伴い,1つのパーセプトロンではXORが再現不能であることを示す.
また,XOR再現可能なニューラルネットワークの構成を示す.
関連する記事
Z3による汎用大域的最適化
http://qiita.com/kotauchisunsun/items/90bce940a1c08ca1b7ae
実装するニューラルネットワーク
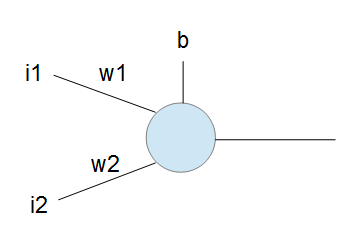
非常に単純なニューラルネットワークで2入力1出力のパーセプトロンを扱う.
出力は
if w1 * i1 + w2 * i2 + b > 0:
return 1
else:
return 0
実際のコード
以下のコードを用いて実行する.
nn_test.py:
# coding:utf-8
import sys
from z3 import *
def and_def(w1,w2,b,s):
for i in [0,1]:
for j in [0,1]:
if i*j==1:
ex = w1 * i + w2 * j + b > 0
else:
ex = w1 * i + w2 * j + b <= 0
print ex
s.add(ex)
print s.check()
print s.model()
def or_def(w1,w2,b,s):
for i in [0,1]:
for j in [0,1]:
if i+j>0:
ex = w1 * i + w2 * j + b > 0
else:
ex = w1 * i + w2 * j + b <= 0
print ex
s.add(ex)
print s.check()
print s.model()
def nand_def(w1,w2,b,s):
for i in [0,1]:
for j in [0,1]:
if not i*j==1:
ex = w1 * i + w2 * j + b > 0
else:
ex = w1 * i + w2 * j + b <= 0
print ex
s.add(ex)
print s.check()
print s.model()
def xor_def(w1,w2,b,s):
for i in [0,1]:
for j in [0,1]:
if i+j==1:
ex = w1 * i + w2 * j + b > 0.0
else:
ex = w1 * i + w2 * j + b <= 0.0
print ex
s.add(ex)
print s.check()
print s.model()
if __name__ == "__main__":
i1 = Real('i1')
i2 = Real('i2')
w1 = Real('w1')
w2 = Real('w2')
b = Real('b')
out = Real('out')
s = Solver()
table = {
"and" : and_def,
"or" : or_def,
"nand" : nand_def,
"xor" : xor_def,
}
table[sys.argv[1]](w1,w2,b,s)
andの場合
| i1 | i2 | 出力 |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
実行するコード
$ python nn_test.py and
> w1*0 + w2*0 + b <= 0
> sat
> [b = 0]
> w1*0 + w2*1 + b <= 0
> sat
> [w2 = 0, b = 0]
> w1*1 + w2*0 + b <= 0
> sat
> [w2 = 0, b = 0, w1 = 0]
> w1*1 + w2*1 + b > 0
> sat
> [w2 = 1, b = -1, w1 = 1]
ということが分かった.したがって,andを表すニューラルネットは,
w1 = 1
w2 = 1
b = -1
で表される.
orの場合
| i1 | i2 | 出力 |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
実行するコード
$ python nn_test.py or
> w1*0 + w2*0 + b <= 0
> sat
> [b = 0]
> w1*0 + w2*1 + b > 0
> sat
> [w2 = 1, b = 0]
> w1*1 + w2*0 + b > 0
> sat
> [w2 = 1, b = 0, w1 = 1]
> w1*1 + w2*1 + b > 0
> sat
> [w2 = 1, b = 0, w1 = 1]
ということが分かった.したがって,orを表すニューラルネットは,
w1 = 1
w2 = 1
b = 0
で表される.
nandの場合
| i1 | i2 | 出力 |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
実行するコード
$ python nn_test.py nand
> w1*0 + w2*0 + b > 0
> sat
> [b = 1]
> w1*0 + w2*1 + b > 0
> sat
> [w2 = 0, b = 1]
> w1*1 + w2*0 + b > 0
> sat
> [w2 = 0, b = 1, w1 = 0]
> w1*1 + w2*1 + b <= 0
> sat
> [w2 = -1, b = 2, w1 = -1]
ということが分かった.したがって,nandを表すニューラルネットは,
w1 = -1
w2 = -1
b = 2
で表される.nandができたので,これをもって,任意の論理回路がニューラルネットワークによって構築可能であることが分かる.
xorの場合
| i1 | i2 | 出力 |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
実行するコード
$ python nn_test.py xor
w1*0 + w2*0 + b <= 0
sat
[b = 0]
w1*0 + w2*1 + b > 0
sat
[w2 = 1, b = 0]
w1*1 + w2*0 + b > 0
sat
[w2 = 1, b = 0, w1 = 1]
w1*1 + w2*1 + b <= 0
unsat
Traceback (most recent call last):
File "nn_test.py", line 73, in <module>
table[sys.argv[1]](w1,w2,b,s)
File "nn_test.py", line 51, in xor_def
print s.model()
File "/usr/lib/python2.7/dist-packages/z3.py", line 6100, in model
raise Z3Exception("model is not available")
z3types.Z3Exception: model is not available
unsatと出力されてしまった.これから1つのパーセプトロンから,xorの構築は不能であることが分かった.
これはxorの出力が線形分離不能なことから起こる問題で,ニューラルネット界隈ではよく知られた問題だ.これがz3を用いても確認できたことが分かる.
2段ニューラルネットワークによるxorの構築
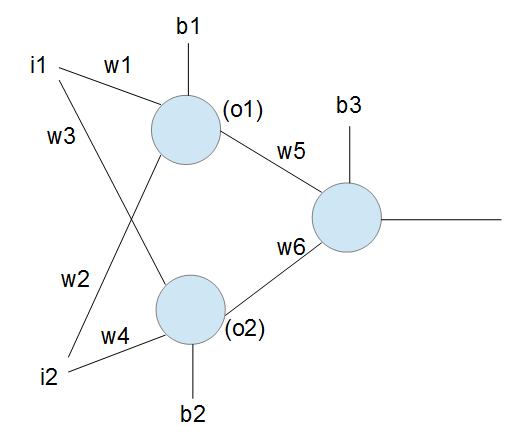
以下のようなニューラルネットワークを考える.
これは入力層を2入力にして,2段にしたニューラルネットワークである.このニューラルネットワークを用いることで,xorが構築できるか確かめる.
xor_nn_test.py:
# coding:utf-8
from z3 import *
if __name__ == "__main__":
w1 = Real('w1')
w2 = Real('w2')
w3 = Real('w3')
w4 = Real('w4')
w5 = Real('w5')
w6 = Real('w6')
b1 = Real('b1')
b2 = Real('b2')
b3 = Real('b3')
s = Solver()
for i in [0.0,1.0]:
for j in [0.0,1.0]:
print "-*-" * 10
o1 = Real('o1%d%d'%(i,j))
o2 = Real('o2%d%d'%(i,j))
o3 = Real('o3%d%d'%(i,j))
s.add(o1 == If(w1 * i + w2 * j + b1 > 0.0 , 1.0, 0.0))
s.add(o2 == If(w3 * i + w4 * j + b2 > 0.0 , 1.0, 0.0))
s.add(o3 == w5 * o1 + w6 * o2 + b3)
if i+j==1:
s.add(o3 > 0.0)
else:
s.add(o3 <= 0.0)
print s.check()
print s.model()
$ python xor_nn_test.py
> -*--*--*--*--*--*--*--*--*--*-
> sat
> [w5 = 0,
> w6 = 0,
> b3 = 0,
> b2 = 1,
> b1 = 1,
> o300 = 0,
> o200 = 1,
> o100 = 1]
> -*--*--*--*--*--*--*--*--*--*-
> sat
> [o301 = 1,
> w4 = 0,
> o300 = 0,
> o201 = 0,
> o101 = 0,
> b3 = 1,
> b2 = 0,
> o200 = 0,
> w5 = -1,
> w2 = -1,
> o100 = 1,
> w6 = 0,
> b1 = 1]
> -*--*--*--*--*--*--*--*--*--*-
> sat
> [o301 = 1,
> w3 = -1,
> o300 = 0,
> o101 = 1,
> b2 = 1,
> o200 = 1,
> w5 = 1,
> o310 = 1,
> w6 = -1,
> b1 = 0,
> w4 = 0,
> o201 = 1,
> b3 = 1,
> w2 = 1,
> o110 = 0,
> o100 = 0,
> o210 = 0,
> w1 = 0]
> -*--*--*--*--*--*--*--*--*--*-
> sat
> [o301 = 1,
> w3 = -1,
> o300 = 0,
> o101 = 1,
> b2 = 2,
> o200 = 1,
> w5 = 1,
> o310 = 1,
> w6 = 1,
> b1 = 0,
> w4 = -1,
> o201 = 1,
> o111 = 1,
> b3 = -1,
> w2 = 1,
> o110 = 1,
> o211 = 0,
> o311 = 0,
> o100 = 0,
> o210 = 1,
> w1 = 1]
satしたことにより,図示したニューラルネットワークでxorが再現できることが分かった.その時の値は
w1 = 1
w2 = 1
w3 = -1
w4 = -1
w5 = 1
w6 = 1
b1 = 0
b2 = 2
b3 = -1
となることが分かる.この係数からニューラルネットワークについて考察を行うと,
左上のニューラルネットワークは
w1 = 1
w2 = 1
b1 = 0
という係数から構成されていることが分かる.この結果,左上のニューラルネットワークは"OR"であることが分かる.
左下のニューラルネットワークは
w3 = -1
w4 = -1
b2 = 2
という係数から構成されていることが分かる.この結果,左下のニューラルネットワークは"nand"であることが分かる.
最後の右のニューラルネットワークは
w5 = 1
w6 = 1
b3 = -1
という係数から構成されていることが分かる.この結果,左下のニューラルネットワークは"and"であることが分かる.
ここで出力をoutとすると
out = (i1 or i2) and not (i1 and i2)
ドモルガン則により,
out = (i1 or i2) and (not i1 or not i2)
out = (i1 and not i1) or (i1 and not i2) or (i2 and not i1) or (i2 and not i2)
ここで
i1 and not i1 = false
i2 and not i2 = false
なので
out = (i1 and not i2) or (i2 and not i1)
out = i1 xor i2
となり,outがi1,i2のxor出力になっていることが,ここからも分かる.
したがって,2段ニューラルネットワークでxor出力をZ3により再現できたことが分かる.
まとめ
Z3により単純なパーセプトロンで,and,or,nandが構築可能であり,nandが構築不能であることを示した.
また,Z3で2段のニューラルネットワークでxorが構築可能であることを示した.また,その部分のパーセプトロンが,and,or,nandと同等の動作を確認し,論理式からもxorが出力されることを示した.