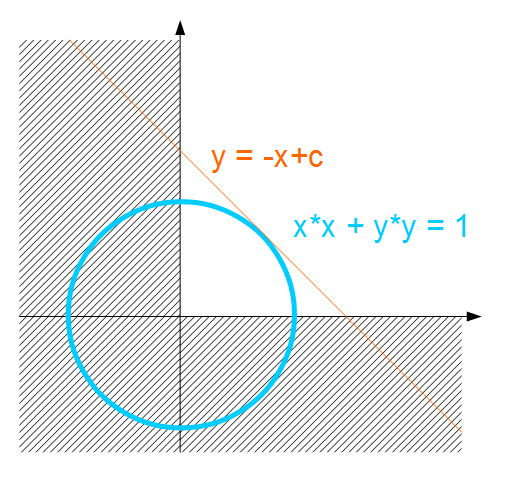概要

Z3 Proverを用いた，"数値的"な大域的最適化手法について示す．

Z3 Proverとは？

ざっくりとはMicrosoft Researchが作った，MITライセンスの定理証明器です．

Z3 is a theorem prover from Microsoft Research. It is licensed under the MIT license.

If you are not familiar with Z3, you can start here.

Z3 can be built using Visual Studio, a Makefile or using CMake. It provides bindings for several programming languages.

See the release notes for notes on various stable releases of Z3.

Z3の魅力

ここまで書いても今一つZ3の意味が分からないと思うので，例を出したいと思います．

コード

from z3 import *

x = Real("x")
y = Real("y")
c = Real("c")

s = Solver()

s.add(
    x > 0,
    y > 0,
    c > 0,
    c * c == 2.0,
    x*x + y*y == 1,
    y == -x + c
)

print s.check()
print s.model()

出力結果

$ python z3_test.py 
> sat
> [x = 0.7071067811?, c = 1.4142135623?, y = 0.7071067811?]

"sat"という文字が出ました．これにより，この制約論理式は充足可能であることが分かります．そして，この制約を充足する変数の組み合わせが出力されています．

一番簡単な例がcです．cは

c > 0
c * c == 2.0

の制約を解け．と書いてあります．ここからc=√2だということが分かります．s.model()の値も，1.4142・・・となっていて正しいことが分かります．
xとyの関係については図を見てもらったほうが早いです．

単位円とy=-x+cの交点を求める問題です．答えは，至極簡単で，x=y=√2/2と答えがわかると思います．（数値的にも正しいことが出力結果からわかります．）
一般的には，y=-x+cをx*x+y*y=1に代入して・・・という数式処理をはさんだり，その解法を人間が考える必要がありますが，Z3ではその必要性はありません．

以上のことより，このZ3は素晴らしい点が３つあることが分かります．

小数を扱うことができる
変数同士の乗除算を扱うことができる
制約条件のみを書くだけで，数式を解く必要がない

これだけあれば大体のことができます．

Z3による大域最適化手順

基本的な思想

　Z3自体に値を最適化する機能はありません．あくまで与えられた論理式が充足するかしないか．充足したときにどのような値をとるか．ということしか，わかりません．
そこで，モデルとデータの誤差に注目します．誤差をどこまで最小化できるか？という命題を解いていきます．それにより，命題が解けない最大の誤差．命題が解ける最小の誤差の値を二分探索で求めます．
これによりZ3により大域最適化を実現することができます．
以下の例では，2x+3にノイズを入れたものをax+bで回帰するモデルを用いて説明します．

テストデータ生成用スクリプト(data.py)

import sys
from random import gauss,seed

seed(0)
n = int(sys.argv[1])

for i in range(n):
    print i,gauss(2.0 * i + 3.0, 0.1)

実行手順

$python data.py 50 > data.csv

残差による大域最適化

データを用意する
モデル式とデータの残差を定義する
残差の2乗の総和(delta)を定義する
モデルをチェックする
4.で求めたdeltaをmax_deltaとする．
min_delta=0.0とする
tmp_delta = (max_delta + min_delta) / 2　とする
delta < max_deltaと定義する
modelがチェックできた場合，max_delta = tmp_deltaとする．
modelがチェック出来なかった場合，8.の定義を取り消し，min_delta = tmp_deltaとする．
max_delta - min_delta < 所望の精度になったとき，終了．そうでなかったとき，8に飛ぶ．

from z3 import *

if __name__ == "__main__":
    data = map(lambda x:map(float,x.split()),open("data.csv")) # 1.

    s = Solver()
    a = Real("a")
    b = Real("b")
    delta = Real("delta")

    deltas = []
    for i,(x,y) in enumerate(data):
        d = Real("d%d"%i)
        deltas.append(d)
        s.add(
            d == y - ( a * x + b )  # 2.
        )
        s.check()

    s.add(delta == sum(d * d for d in deltas)) # 3.

    print s.check() # 4.
    print s.model()

    max_delta = float(s.model()[delta].as_decimal(15)[:-1]) # 5.
    min_delta = 0                                           # 6.

    while 1:
        tmp_delta = (max_delta + min_delta) / 2.0           #7.
        s.push()

        s.add( delta < tmp_delta )   # 8.

        if s.check() == sat: # 9.
            print "sat:",tmp_delta,min_delta,max_delta
            s.push()
            max_delta = tmp_delta
        else: # 10.
            print "unsat:",tmp_delta,min_delta,max_delta
            s.pop()
            min_delta = tmp_delta

        if max_delta - min_delta < 1.0e-6: # 11.
            break

    print s.check()
    model = s.model()

    print delta,model[delta].as_decimal(15)
    print a,model[a].as_decimal(15)
    print b,model[b].as_decimal(15)

結果

delta 0.604337347396090?
a 2.001667022705078?
b 2.963314133483435?

a=2.0,b=3.0に近い数字が求められていることが分かります．

個別のケースの境界領域に対する大域最適化

データを用意する
epsilon > 0と定義する
それぞれのデータのケースによって，制御変数(x)・目的変数(y)，モデルをy=f(x)としたとき，y - epsilon <= f(x) <= y + epsilonを定義する．
モデルをチェックする
4.で求めたepsilonをmax_epsilonとする．
min_epsilon=0.0とする
tmp_epsilon = (max_epsilon + min_epsilon ) / 2　とする
epsilon < max_epsilonと定義する
modelがチェックできた場合，max_epsilon = tmp_epsilonとする．
modelがチェック出来なかった場合，8.の定義を取り消し，min_epsilon = tmp_epsilonとする．
max_epsilon - min_epsilon < 所望の精度になったとき，終了．そうでなかったとき，8に飛ぶ．

from z3 import *

if __name__ == "__main__":
    data = map(lambda x:map(float,x.split()),open("data.csv")) # 1.

    s = Solver()
    a = Real("a")
    b = Real("b")
    epsilon = Real("epsilon")

    s.add(epsilon >= 0.0) # 2.

    for i,(x,y) in enumerate(data):
        s.add(
            y - epsilon <=  ( a * x + b ) , (a*x+b) <= y + epsilon # 3.
        )
        s.check() 

    print s.check() # 4.
    print s.model()

    max_epsilon = float(s.model()[epsilon].as_decimal(15)[:-1]) # 5.
    min_epsilon = 0 # 6.

    while 1:
        tmp_epsilon = (max_epsilon + min_epsilon) / 2.0 # 7.
        s.push()

        s.add( epsilon < tmp_epsilon ) # 8.

        if s.check() == sat: # 9.
            print "sat:",tmp_epsilon,min_epsilon,max_epsilon
            s.push()
            max_epsilon = tmp_epsilon
        else: # 10.
            print "unsat:",tmp_epsilon,min_epsilon,max_epsilon
            s.pop()
            min_epsilon = tmp_epsilon

        if max_epsilon - min_epsilon < 1.0e-6: # 11.
            break

    print s.check()
    model = s.model()

    print epsilon,model[epsilon].as_decimal(15)
    print a,model[a].as_decimal(15)
    print b,model[b].as_decimal(15)

結果

epsilon 0.223683885406060?
a 2.000628752115151?
b 3.006668013951515?

こちらもa=2.0,b=3.0に近い数字が求められていることが分かります．

どちらの手法を使うべきか

後者の"個別のケースの境界領域に対する大域最適化"です．
　1つは早さです．前者は一度一度checkを行う時間が長いです．これはおそらくZ3の内部実装の話なので，詳しくは分かりませんが，deltaとx,yの関係が非線形性の強い対応しているので，時間がかかっていると思われます．一方で，epsilonとx,yは非線形性が弱い対応をしているため，時間がかからないと思われます．
　2つめはモデルの合理性の判断のしやすさです．これは"epsilon < 指定の精度"という風に先に制約を加えておくことで，モデルが指定の精度を満たさなかったとき，unsatになるため，ダメなモデルの検知が速くなります．また，先に制約を加えて置く他のメリットも大きく，新たにデータが追加されても，こちらが指定した精度は保証されるので，非常に使いやすいです．
　"残差による大域最適化"はあくまで既存の方法も使える．程度の説明です．個人的には，人間が数式を整理するうえで前者は扱いやすかっただけであって，Z3で処理する分には後者の手法のほうが良いように思います．

大域的最適化という議論

　この手法は大域的最適化ではない．と思われるかもしれません．半分Yesで，半分Noです．それは立場によるもので，コンピュータの立場か，数学の立場です．おそらく２つの主張があるのではないかと思ってます．
　1つは誤差の点です．例えば，√2という数字があります．これは数学的には表現されていますが，一般的なコンピュータ上で表現できません．コンピュータでは有理数しか取り扱うことができません．そのため，√2という数字を完璧に扱う手段は通常ありません．そのため，64bitの浮動小数点では1e-15程度の誤差の範囲で√2を近似して取り扱っています．したがって，コンピュータ上では数学的に厳密な√2は存在しません．しかし，これは個人的にはどうでもよい話です，いくら手計算で限界まで数式をきれいに整理し，読みやすい形にしたとしても数値まで落とさないとプログラム的に利用できません．そのため，有理数と無理数の誤差，もしくは数学的に表現される数値とコンピュータ上で表現される数値はプログラム上許容されなければなりません（許容されるように組むべきです）．今までも，しかたなく許容したり，もしくは言われるまで許容されることを気づかなかったレベルなので実用上問題はないと思います．
　2つ目は公式ではない．ということです．題名を見て，おそらくは二次方程式の解の公式のようなものを頭に浮かべられる方もおられると思います．限定的な数式の上で，限定的な数値の範囲で限定的な解を求めることができる．というのが一般的な解の公式だと思います．これはどちらかというとアルゴリズムに近いもので，数式というより手続きにすぎません．もちろんZ3　Proverの実装が間違っていない前提で作られたものなので，この手続きが必ずしも正しい値を導くかどうかは私は分かりません．しかし，いくつかの例を持って最適であろう解を実際に提示できたことに意味があると思います．
　おそらくこの手法は数学的には，不自然な点も多いかもしれませんが，コンピュータ的には実用上特に問題がないと思われます．したがって，ここでは"数学的"な大域的最適化ではなく，あくまで"数値的"な大域最適化と表現しています．

Z3による大域最適化の魅力

コードを見てもらえばわかると思いますが，数式を定義するのみで最適化できることです．
機械学習において苦しい点は，"数式の立式"と"数式の解析"だと思っています．前者は問題が与えられたとき，割とすんなりとできます．ただセットで"数式の解析"も必要となってきます．目的関数の勾配をいかに計算するか・・・勾配を計算できないために，目的関数の形を変える・・・等々，泥臭い数式自体の変形をする必要があり，長年頭が痛い問題でした．ただ，Z3 Proverでの最適化手法を思いついてから，そういう時代でもないのかな．という気がして来ました．

数式処理システムとの違い

数式処理システムで有名どころはMathematica，Maple，OSSではMaxima.マイナーどころではPySimやらSage等があります．私自身，Maximaを使っていましたが，個人的には満足することができませんでした．
特にMaximaは，不等式の扱いが弱かったり，複雑な式を入れすぎると，3日待った挙句，エラーで答えが返ってこない．といったことがありました．また答えが返ってきたとしても，Maximaが数式で扱おうとしすぎて，理解不能な答えを返してくることもありました．プログラマ的には数学の真理に興味はなく，与えられた数式の数値解だけ出てくれれば満足なことも多いです．その意味で複雑な数式を入れても，答えを返すことができて，PythonバインドがあるZ3は，かなりありがたい存在です．(もうMaximaの数式をパースしてプログラムに変換する処理なんか書きたくない)

Z3による大域最適化の課題

とにかく遅いです．何度かいろいろ試したことがありますが，厳しいこともあります．このZ3を用いて，ニューラルネットワークの全変数の最適化をかけたことがありますが，3日かけても返ってこないこともありました．また，たまに小数の表現の限界を突破することがあるらしく，その場合，例外を吐いて死ぬこともあります．そのため，いくら非線形の大域最適化ができるとはいえ，やりすぎるとモデルをチェックすらできなくなることも，ままあります．このように発展段階かもしれませんが，数式をそのままプログラムに入れて，勝手に大域最適化してくれる手法としては，かなり魅力的な手法であると思います．

Z3による汎用大域的最適化

概要